哈夫曼编码详解——图解真能看了秒懂
因为初学哈夫曼编码时间有些长了,难免会忘记,后上网查了下很多不能让我一下子回忆起这个编码具体实现步骤。现在懂了之后来总结一下,让跟我一样的人能快速回忆。
直接上题目:
已知字符集{ a, b, c, d, e, f },若各字符出现的次数分别为{ 6, 3, 8, 2, 10, 4 },则对应字符集中各字符的哈夫曼编码可能是:(2分)
A. 00, 1011, 01, 1010, 11, 100
B. 00, 100, 110, 000, 0010, 01
C. 10, 1011, 11, 0011, 00, 010
D. 0011, 10, 11, 0010, 01, 000
步骤一:
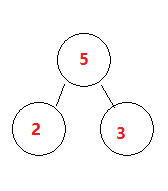
1.找最小两个次数(这里是2和3)
2.把他们放进树中(小左大右)
3.每次组合都多一个父节点(即2+3=5)
步骤二:
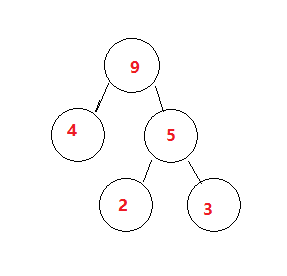
1.再选出2个最小的数(排除上面已经选了的)——选出了4和6
2.因为4<5 , 6>5(5为步骤一中组合后的父节点)
3.单独拿4来跟5组合(小左大右) 【如果拿出的2个数都比5小,则这2个数自己组合后跟5组合,下面提到】
步骤三:
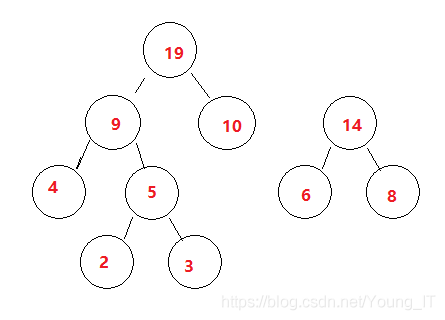
1.因为步骤二用掉了4,还没用6。现在取最小2个数
2.因为6 < 9 , 8< 9 所以6和8自己组合(小左大右) (组合后先放一边)
步骤四:
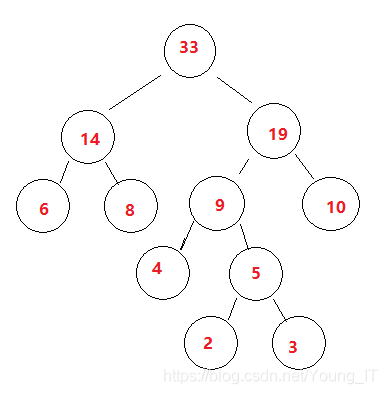
1.取出最后10
2.10要和这两个子树根节点最小的组合(9<14,所以和9组合)(小左大右)
3.然后把14的子树组合上去(小左大右) 所以放左边
步骤五:
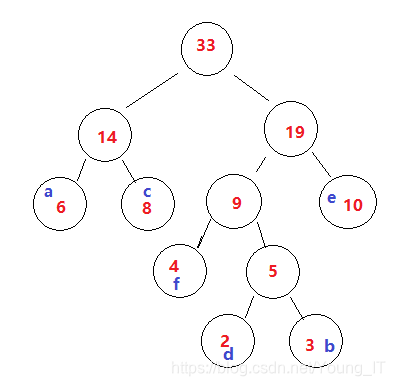
组合完哈夫曼树后,将对应的字符填上去
步骤六:
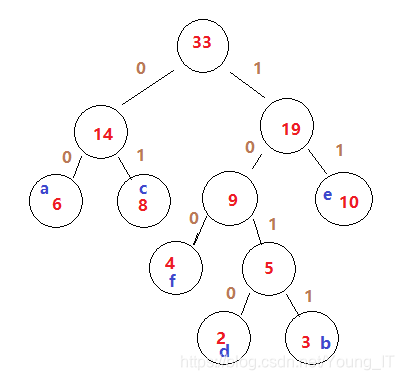
从根节点开始向下走往左为0,往右1。走到对应的字符的路径就是该字符的哈夫曼编码(左0右1)
最后结果:
| 字符 | 哈夫曼编码 |
| a | 00 |
| b | 1011 |
| c | 01 |
| d | 1010 |
| e | 11 |
| f | 100 |
所以最后答案 A
已知字符集{ a, b, c, d, e, f },若各字符出现的次数分别为{ 6, 3, 8, 2, 10, 4 },则对应字符集中各字符的哈夫曼编码可能是:(2分)
A. 00, 1011, 01, 1010, 11, 100 ✔
B. 00, 100, 110, 000, 0010, 01
C. 10, 1011, 11, 0011, 00, 010
D. 0011, 10, 11, 0010, 01, 000
我觉得我讲明白了。
不知道你们有没有秒懂!哈哈哈。
如果我有哪里出错,或是不懂的地方 欢迎评论留言。