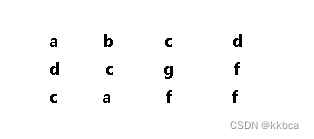牛客 JZ12矩阵中的路径 (剑指offer第12题)(非递归处理简单易懂版)
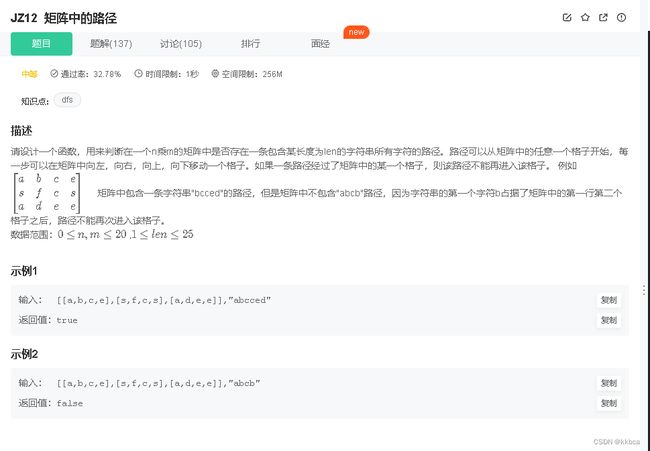
JZ12矩阵中的路径
我相信,对于这道题,非递归会比递归更加好理解一点。
我想了很久才做出来,感觉自己还挺厉害哈哈哈哈哈。
对于这道题,基本上是有很多条路径的,只要字符匹配上了,就可以往这个方向走,有时候会有好几个字符同时匹配上,因此路径会不止一条,并且这条路径已经走过的节点不能再去走,当然这只限制一条,你如果换一条路径,上面这个限制又会重新开始。读完题意,我们来讲解一下思路。
首先,你得需要保存当前的位置能走没有越界且字符匹配的位置(这步主要是为了当前节点走不通,返回到另一条匹配的路再走)
比如有如下这个矩阵。
我们目标l路径是“abca”,但是如果我们先往右走了, 走出了abcd,才会发现不匹配。
那么你需要能够返回到坐标为(1,1)的c继续走,因为前面我已经判断过了,走出了 “ab” 是符合要求的。
有这么一个目标,那么我可以使用栈来处理,先将匹配到的第一个字符坐标压入栈中,又以这个坐标为基点,往左走,往右走,往上走,往下走,如果能走通,并且匹配上了字符,那么我就可以将他添加入栈,只要符合,有几个我就加几个,来防止此路不通的情况,这使我们能够返回。
这里我使用了pair
stack>s; //s存放位置(x和y) 但是,由于会出栈的情况,你并不知道当前结点已经走过几个字符了,如下图中的数字,不知道该匹配的下一个字符索引值,因此我们还需要一个stack
stack sword;//sword存放word的索引,看和word的第几个作对比 其他处理都差不多了,但是我们还没有处理当前走过路径的问题,走过的路径是不能再次走的。 因此我们还需要一个容器来存储当前走过的路径,并保证不再踏入该路径。只药走过的路径添加到容器里即可,因此使用vector就很合适,类型依然是pair
vector> v;//v存放走过的路径 给定的函数如下,遍历二维数组的每一个元素 if(martix[i][j]==word[0]) 这句代码证明当前元素和路径的第一个字符匹配,也就是当前元素为路径的开头,我们就可以开始往后面走。使用栈来处理,先将当前元素压入栈s,同时还要将当前匹配的是第几个字符压入栈sword。
这里还有一局for循环来删除之前所走的不可行路径,因为如果路径v不删除,返回到另一条路径时发生明明我这条路径还没走过这个结点,你就不让我走了。刚刚好我们也将当前是第几个字符存储到sword,取出来时,就可以用循环删除掉后面多余的路径。
然后我们将该路径放入vector v 里面,同时判断 if(v.size()==word.size()) 他们长度是否相等,如果相等,证明该路径匹配且走完,那么我们返回true即可,但是这里我们是怎么判断是路径一定匹配的呢?这里还不懂如何是一定匹配上的没关系,我们来看下面是如何进栈的。
if (p.first + 1 < n && matrix[p.first+1][p.second] == word[wordi+1]) 这句代码是来判断往下走的这条路径是不是有效(是不是有越阶),并且字符是否匹配,如果没有越阶且匹配,那么我们就要去cheek函数里面判断这条路径我们是否已经走过,这里就是将vector
//checkPath检查这条路径是否在之前被经过
void checkPath(pair p,int wordi) {
for (int k = 0; k < v.size(); k++) {
if (p == v[k]) {
return;
}
}
s.push(p);
sword.push(wordi + 1);
} 那么我们将上下左右走的每一个路径都判断合不合法,然后查看是否入栈,这样代码就可以跑起来了,如果s为空都没匹配上,证明这个开头点不行,我们就遍历二维数组查看是否有新的开头点,有就继续跑,没有就返回false,结束该程序。
bool hasPath(vector >& matrix, string word) {
// write code here
int n = matrix.size();
int m = matrix[0].size();
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (matrix[i][j] == word[0]) {
s.push(make_pair(i, j));
sword.push(0);
//s非空证明这条路径还没遍历完
while (!s.empty()) {
pair p = s.top();
int wordi = sword.top();
//将之前走过的不可行路径删除
for(int k = wordi;k= 0 && matrix[p.first-1][p.second] == word[wordi+1]){
checkPath(make_pair(p.first-1,p.second), wordi);
}
if(p.second + 1 < m && matrix[p.first][p.second+1] == word[wordi+1]){
checkPath(make_pair(p.first,p.second+1), wordi);
}
if(p.second - 1 >=0 && matrix[p.first][p.second-1] == word[wordi+1]){
checkPath(make_pair(p.first,p.second-1), wordi);
}
}
}
}
}
return false;
} 总代码如下
#include
#include
#include
class Solution {
public:
//s存放位置(i和j)
stack>s;
//sword存放word的索引,看和word的第几个作对比
stack sword;
//v存放当前路径
vector> v;
//checkPath检查这条路径是否在之前被经过
void checkPath(pair p,int wordi) {
for (int k = 0; k < v.size(); k++) {
if (p == v[k]) {
return;
}
}
s.push(p);
sword.push(wordi + 1);
}
bool hasPath(vector >& matrix, string word) {
// write code here
int n = matrix.size();
int m = matrix[0].size();
for (int i = 0; i < matrix.size(); i++) {
for (int j = 0; j < matrix[0].size(); j++) {
if (matrix[i][j] == word[0]) {
s.push(make_pair(i, j));
sword.push(0);
//s非空证明这条路径还没遍历完
while (!s.empty()) {
pair p = s.top();
int wordi = sword.top();
//将之前走过的不可行路径删除
for(int k = wordi;k= 0 && matrix[p.first-1][p.second] == word[wordi+1]){
checkPath(make_pair(p.first-1,p.second), wordi);
}
if(p.second + 1 < m && matrix[p.first][p.second+1] == word[wordi+1]){
checkPath(make_pair(p.first,p.second+1), wordi);
}
if(p.second - 1 >=0 && matrix[p.first][p.second-1] == word[wordi+1]){
checkPath(make_pair(p.first,p.second-1), wordi);
}
}
}
}
}
return false;
}
}; 希望我已经讲明白了,如果有不懂的地方,或者我的逻辑不好理解的地方,可与在评论区指出来,我都会看的,谢谢大家!!!!!!!
如果可以的话就点个赞吧,那就更感谢了。。。