从基础到卷积神经网络（第12天）

1. PyTorch 神经网络基础

1.1 模型构造

1. 块和层

首先，回顾一下多层感知机

import torch 
from torch import nn
from torch.nn import functional as F

net = nn.Sequential(nn.Linear(20, 256), nn.ReLU(), nn.Linear(256, 10))

X = torch.rand(2, 20) # 生成随机输入（批量大小=2， 输入维度=20）
net(X) # 输出（批量大小=2, 输出维度=10）

2. 自定义块

自定义MLP实现上一节的功能

class MLP(nn.Module): # 定义nn.Mudule的子类
    def __init__(self): 
        super().__init__() # 调用父类
        self.hidden = nn.Linear(20, 256) # 定义隐藏层
        self.out = nn.Linear(256, 10) # 定义输出层
        
    def forward(self, X): # 定义前向函数
        return self.out(F.relu(self.hidden(X))) # X-> hidden-> relu-> out

实例化MLP的层，然后再每次调用正向传播函数时调用这些层

net = MLP()
net(X)

3. 实现Sequential类

class MySequential(nn.Module):
    def __init__(self, *args):
        super().__init__()
        for block in args:
            self._modules[block] = block
        
    def forward(self, X):
        for block in self._modules.values():
            X = block(X)
        return X

net = MySequential(nn.Linear(20, 256), nn.ReLU(), nn.Linear(256, 10))
net(X)

4. 在正向传播中执行代码

class FixedHiddenMLP(nn.Module):
    def __init__(self):
        super().__init__()
        self.rand_weight = torch.rand((20, 20), requires_grad=False) # 加入随机权重
        self.linear = nn.Linear(20, 20)

    def forward(self, X):
        X = self.linear(X)
        X = F.relu(torch.mm(X, self.rand_weight) + 1) # 输入和随机权重做矩阵乘法 + 1（偏移）-》激活函数
        X = self.linear(X)
        while X.abs().sum() > 1: # 控制X小于1
            X /= 2
        return X.sum() # 返回一个标量

net = FixedHiddenMLP()
net(X)

5. 混合搭配各种组合块的方法

class NestMLP(nn.Module):
    def __init__(self):
        super().__init__()
        self.net = nn.Sequential(nn.Linear(20, 64), nn.ReLU(),
                                 nn.Linear(64, 32), nn.ReLU())
        self.linear = nn.Linear(32, 16)
    
    def forward(self, X):
        return self.linear(self.net(X)) # 输入-> net-> linear中

chimera = nn.Sequential(NestMLP(), nn.Linear(16, 20), FixedHiddenMLP()) # (32, 16)->(16, 20) ->(20, 1)
chimera(X)

总结：
1、在init中写各种层
2、在前向函数中调用init中各种层
有很强的灵活性

1.2 参数构造

具有单隐藏层的MLP

import torch
from torch import nn

net = nn.Sequential(nn.Linear(4, 8), nn.ReLU(), nn.Linear(8, 1))
X = torch.rand(size=(2, 4))
net(X)

参数访问

print(net[2].state_dict()) # 拿到nn.Linear的相关参数

访问目标参数

print(type(net[2].bias))
print(net[2].bias)
print(net[2].bias.data)
net[2].weight.grad == None # 梯度是否为0，因为此时还没有计算，所以没有梯度

一次访问所有参数

print(*[(name, param.shape) for name, param in net[0].named_parameters()])
print(*[(name, param.shape) for name, param in net.named_parameters()])

输出没有block1是因为第二层是ReLU是没有参数的

net.state_dict()['2.bias'].data # 访问最后一层的偏移

从嵌套块收集参数

def block1():
    return nn.Sequential(nn.Linear(4, 8), nn.ReLU(), 
                         nn.Linear(8, 4), nn.ReLU())

def block2(): # block2嵌套4个block1
    net = nn.Sequential()
    for i in range(4): 
        net.add_module(f'block {i}', block1()) 
    return net

rgnet = nn.Sequential(block2(), nn.Linear(4, 1))
rgnet(X)

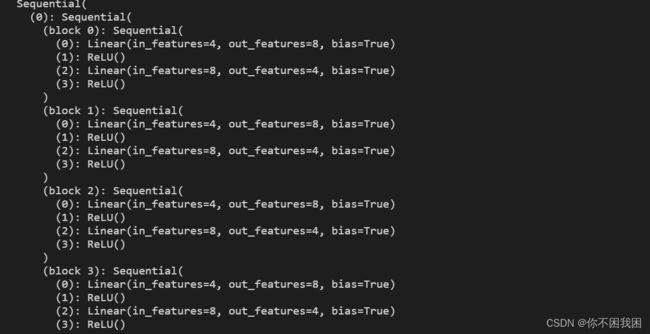
print(rgnet) # 查看网络结构

内置初始化

def init__normal(m): # 传入的module
    if type(m) == nn.Linear: # 如果传入的是全连接层
        nn.init.normal_(m.weight, mean=0, std=0.01) # 内置初始化，均值为0方差为1，.normal_替换函数不返回
        nn.init.zeros_(m.bias) # 所有的bias赋0

net.apply(init__normal) # 对神经网络模型net中的所有参数进行初始化，使用init_normal()函数对参数进行随机初始化
net[0].weight.data[0], net[0].bias.data[0]

def init_constant(m):
    if type(m) == nn.Linear:
        nn.init.constant_(m.weight, 1) # 将m.weight初始常数化为1
        nn.init.zeros_(m.bias)

net.apply(init_constant)
net[0].weight.data[0], net[0].bias.data[0]

不建议权重全部常数化，会导致所有向量向一致的方向发展

对某些块应用不同的初始化方法

def xavier(m):
    if type(m) == nn.Linear:
        nn.init.xavier_uniform_(m.weight) # 使用Xavier均匀分布进行初始化

def init_42(m):
    if type(m) == nn.Linear:
        nn.init.constant_(m.weight, 42)

net[0].apply(xavier) # 第一个层用xavier初始化
net[2].apply(init_42) # 第二个层用init_42进行初始化
print(net[0].weight.data[0])
print(net[2].weight.data)