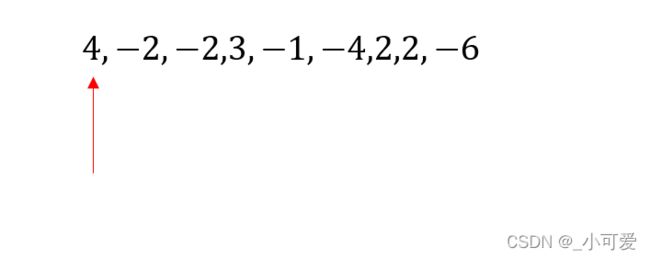线段树与区间最大子段和问题,这一篇就够了
1、经典的区间最大子段和问题
问题描述:给定一个序列 a 1 , a 2 , a 3 , . . a n a_1,a_2, a_3,..a_n a1,a2,a3,..an,如何求出该序列的最大子段和?(询问的区间个数为 m m m)
解决方案:
- 暴力统计:对于每一个区间 [ l , r ] [l,r] [l,r],每一次选定一个子段的起点,然后枚举子段的长度,算法复杂度为 O ( m n 2 ) O(mn^2) O(mn2)。
- 动态规划:我们一次性算出所有的区间的最大子段和,然后使用直接询问答案。我们规定:
- l s \color{Green}ls ls: 表示区间紧靠左端点的子段的最大和
- r s \color{Blue}rs rs: 表示区间紧靠右端点的子段的最大和
- m s \color{OrangeRed}ms ms: 表示区间子段的最大和
- s \color{Blue}s s:表示区间子段和。
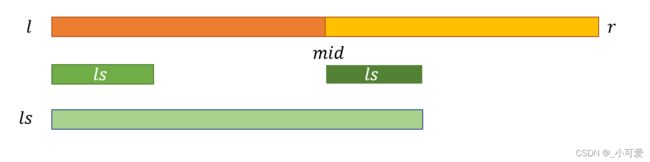
假设一个区间为 [ l , r ] [l,r] [l,r],我们将它一分为二,并且我们假设已经得到了左边区间和右边区间的各自的四样所有信息,那么我们如何求出这个区间的的四个信息呢?
显然有:
s = s l + s r s=s_l+s_r s=sl+sr

求解 l s ls ls,那么我们有两个选择,选择左边区间的 l s ls ls,或者是把左边区间全部选了然后再选取右边区间的 l s ls ls。因为子段必须保持连续性,所以这两个选择是最优的。
l s = m a x ( l s l , s l + l s r ) ls=max(ls_l, s_l+ls_r) ls=max(lsl,sl+lsr)
同样道理求解 r s rs rs,那么我们有两个选择,选择右边区间的 r s rs rs,或者是把右边区间全部选了然后再选取左边区间的 r s rs rs。因为子段必须保持连续性,所以这两个选择是最优的。
r s = m a x ( r s r , s r + r s l ) rs=max(rs_r, s_r+rs_l) rs=max(rsr,sr+rsl)
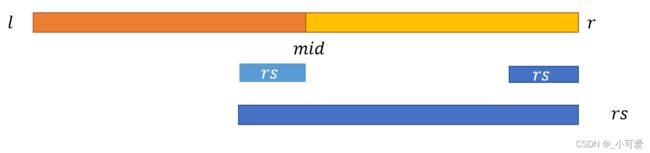
求解 m s ms ms,那么我们有两个选择,选择右边区间的 m s ms ms,或者是左边区间的 m s ms ms,或者是左边区间的 r s rs rs和右边区间的 l s ls ls的和,因为选择保证了连续子段的连续性,所以最优解一定在上面三种选择中。
m s = m a x ( m s r , m s r , r s l + l s r ) ms=max(ms_r, ms_r, rs_l+ls_r) ms=max(msr,msr,rsl+lsr)
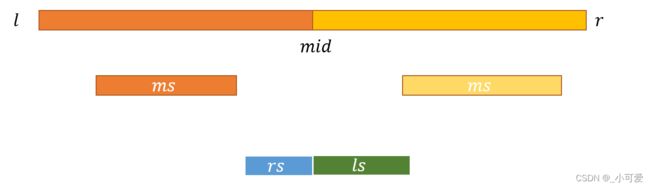
到此,我们完成了区间合并的工作,那么我们就可以使用区间合并的方式进行动态规划。
#include 由上面的代码可知,合并的区间越来越大,第一轮合并的区间为 n n n个,第二轮合并的区间为 n 2 \dfrac{n}{2} 2n个,第三轮合并的区间为 n 4 \dfrac{n}{4} 4n个,所以总的合并区间个数约为 2 n 2n 2n个,总的复杂度为: O ( n + m ) O(n+m) O(n+m),非常优秀!
- 线段树:我们可以使用动态规划可以非常快速地一次性算出所有的区间的最大子段和,然后使用直接询问答案。但是如果操作带修改的序列时,又如何设计更好的算法?那么线段树就可以大显神通了!如果你学过线段树,你就会发现这个问题真的是和线段树天生一对啊!区间合并,单点修改,优秀的 O ( log n ) O(\log n) O(logn)的复杂度!
下面是推荐的练习的题目:SP1716
A C C o d e \color{Green}{AC} \, \color{Red}{Code} ACCode
#include 复杂度分析:查询操作复杂度为 O ( log n ) O(\log n) O(logn), 修改的复杂度为 O ( log n ) O(\log n) O(logn),总的复杂度为 O ( n + m log n ) O(n+m\log n) O(n+mlogn)。下面所有的变形问题,我们都使用线段树解决。
2、区间最大子段和变形问题1
问题描述:给定一个序列 a 1 , a 2 , a 3 , . . a n a_1,a_2, a_3,..a_n a1,a2,a3,..an,给定 m m m个区间组合,对于每一个区间组合 [ x 1 , y 1 ] , [ x 2 , y 2 ] [x_1,y_1], \, [x_2, y_2] [x1,y1],[x2,y2],问对于左端点在 [ x 1 , y 1 ] [x_1,y_1] [x1,y1]并且右端点在 [ x 2 , y 2 ] [x_2,y_2] [x2,y2]的所有区间的最大子段和。
解决方案:其实就是经典最大子段和问题的一个小变形,我们可以把区间组合的两个区间进行分类讨论:
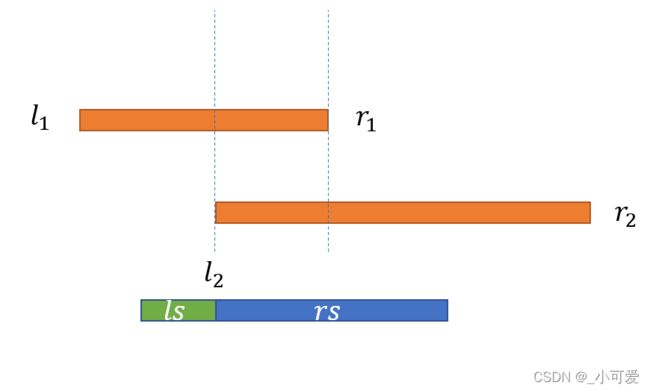
- 两个区间没有交集,那么这时候很好办,因为要满足子段的连续的特性,所以中间的一段是必须要选择的,因此最优解就是:
m s = s u m ( r 1 , l 2 ) + r s l 1 , r 1 + l s l 2 , r 2 ms=sum(r_1, l_2)+rs_{l_1, r_1}+ls_{l_2, r_2} ms=sum(r1,l2)+rsl1,r1+lsl2,r2
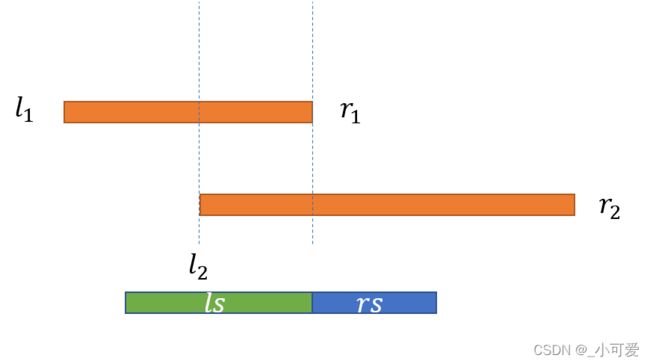
- 两个区间有交集,那么也可以分为三种情况:
- 子段只在区间 [ l 2 , r 1 ] [l_2,r_1] [l2,r1]中,此时的最大值为 m s 1 = m s l 2 , r 1 ms_1=ms_{l_2,r_1} ms1=msl2,r1
- 子段不只是在区间 [ l 2 , r 1 ] [l_2,r_1] [l2,r1]中,为了满足连续性,所以必定是一头选左最大子段和,一头选右最大子段和:
- 第一种情况 m s 2 = l s l 1 , l 2 + r s l 2 + 1 , r 2 ms_2=ls_{l_1,l_2}+rs_{l_2+1, r_2} ms2=lsl1,l2+rsl2+1,r2
- 第二种情况 m s 3 = l s l 1 , r 1 + r s r 1 + 1 , r 2 ms_3=ls_{l_1,r_1}+rs_{r_1+1, r_2} ms3=lsl1,r1+rsr1+1,r2
因此有最后的答案为:
m s = m a x ( m s 1 , m s 2 , m s 3 ) ms=max(ms_1,ms_2,ms_3) ms=max(ms1,ms2,ms3)
这也恰好对应了线段树的查找答案的方法!
例题:SP2916
A C C o d e \color{Green}{AC} \, \color{Red}{Code} ACCode
#include 3、区间最大子段和变形问题2
问题描述:给定一个序列 a 1 , a 2 , a 3 , . . a n a_1,a_2, a_3,..a_n a1,a2,a3,..an,有 m m m个区间,求出每一个对应区间的最大子段和,但是区间中所有相同的数只能算一次。
例题:SP1557
解决方案: 这个问题虽然看起来和经典的最大子段和问题极其相似,但是如果按照经典的思路进行动态规划,区间合并,那么将会很难统计,因为所有相同的数字只能统计一次,会牵扯到判重的问题。区间判重是个相当不简单的任务,因此要另辟思路。
某位巨佬说过,在你感觉一切都没有思路的时候,排序一定可以帮到你。
因此,我们使用离线算法,把所有的询问区间按照右边界大小从小到大排序,然后线性扫描并且更新线段树。但是我们现在先不管这里询问的事情,暂且放下,现在最重要的是我们如何去判重,并且如何维护最大子段和?
我们假定有下面这个序列:
4 , − 2 , − 2 , 3 , − 1 , − 4 , 2 , 2 , − 6 4, -2 ,-2, 3 ,-1, -4, 2, 2, -6 4,−2,−2,3,−1,−4,2,2,−6
规定:
- s u m i sum_i sumi:以位置 i i i起始的子段和。
- h i s m a x i hismax_i hismaxi:以位置 i i i起始的最大子段和。
- t a g i tag_i tagi:以位置 i i i起始的增加的子段和。
- h i s m a x t a g i hismaxtag_i hismaxtagi:以位置 i i i起始的增加的最大子段和。
注意:两个 t a g tag tag数组是为了后面的线段树的更新操作,是标记操作的基础。假设当前线性扫描到了 1 1 1的位置。
并且可以注意到在线性扫描的过程中, s u m i sum_i sumi的值是一直在变化的, h i s m a x i hismax_i hismaxi就是 s u m i sum_i sumi出现过的最大的值,同理, t a g i tag_i tagi的值是一直在变化的, h i s m a x t a g i hismaxtag_i hismaxtagi就是 t a g i tag_i tagi出现过的最大的值。
| i i i | s u m sum sum | h i s m a x hismax hismax | t a g tag tag | h i s m a x t a g hismaxtag hismaxtag |
|---|---|---|---|---|
| 1 1 1 | 4 4 4 | 4 4 4 | 0 0 0 | 0 0 0 |
| 2 2 2 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 |
| 3 3 3 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 |
| 4 4 4 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 |
| i i i | s u m sum sum | h i s m a x hismax hismax | t a g tag tag | h i s m a x t a g hismaxtag hismaxtag |
|---|---|---|---|---|
| 1 1 1 | 4 − 2 = 2 4-2=2 4−2=2 | 4 4 4 | − 2 -2 −2 | 0 0 0 |
| 2 2 2 | − 2 -2 −2 | − 2 -2 −2 | 0 0 0 | 0 0 0 |
| 3 3 3 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 |
| 4 4 4 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 |
| i i i | s u m sum sum | h i s m a x hismax hismax | t a g tag tag | h i s m a x t a g hismaxtag hismaxtag |
|---|---|---|---|---|
| 1 1 1 | 4 − 2 − 2 = 0 4-2-2=0 4−2−2=0 | 4 4 4 | − 2 − 2 = − 4 -2-2=-4 −2−2=−4 | 0 0 0 |
| 2 2 2 | − 2 − 2 = − 4 -2-2=-4 −2−2=−4 | − 2 -2 −2 | − 2 -2 −2 | 0 0 0 |
| 3 3 3 | − 2 -2 −2 | − 2 -2 −2 | 0 0 0 | 0 0 0 |
| 4 4 4 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 |
| i i i | s u m sum sum | h i s m a x hismax hismax | t a g tag tag | h i s m a x t a g hismaxtag hismaxtag |
|---|---|---|---|---|
| 1 1 1 | 4 − 2 − 2 + 3 = 3 4-2-2+3=3 4−2−2+3=3 | 4 4 4 | − 2 − 2 + 3 = − 1 -2-2+3=-1 −2−2+3=−1 | 0 0 0 |
| 2 2 2 | − 2 − 2 + 3 = − 1 -2-2+3=-1 −2−2+3=−1 | − 1 -1 −1 | − 2 + 3 = 1 -2+3=1 −2+3=1 | 1 1 1 |
| 3 3 3 | − 2 + 3 = 1 -2+3=1 −2+3=1 | 1 1 1 | 3 3 3 | 3 3 3 |
| 4 4 4 | 3 3 3 | 3 3 3 | 0 0 0 | 0 0 0 |
到这里,应该很容易明白了吧! t a g i tag_i tagi值就是从 i i i后面开始加上去的一段和, h i s m a x i hismax_i hismaxi表示的就是从 i i i开始的最大子段和,也是 s u m i sum_i sumi出现过的最大值,并且有:
{ h i s m a x i = h i s m a x t a g i + v a l i s u m i = t a g i + v a l i \begin{cases} hismax_i=hismaxtag_i+val_i\\sum_i=tag_i+val_i\end{cases} {hismaxi=hismaxtagi+valisumi=tagi+vali
那么如何搞定重复统计的问题?其实这个问题可以从贡献的角度去考虑,说到这里,其实有一个非常巧妙统计的技巧,我会在另一篇文章给出。 从贡献的角度去考虑重复统计的问题,那么事情就变得简单很多了,举例说明。

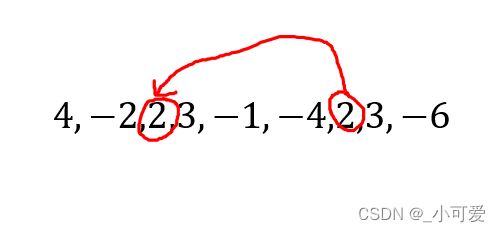
图中的数字 2 2 2有两个,一个在位置 3 3 3, 一个在位置 7 7 7,那么进行统计的时候,我们可以看到,对于区间 [ 1 , 3 ] [1,3] [1,3]都是有一个 2 2 2的,所以这个位置 7 7 7的 2 2 2对它们的 s u m i sum_i sumi贡献为零,然而它对区间 [ 4 , 7 ] [4,7] [4,7]都是有贡献的,因此我们在统计的时候先预处理一下。
规定:
-
p r e i pre_i prei:表示值等于 v a l i val_i vali最近的一次扫描过的位置,比如上面的例子 p r e 7 = 2 pre_7=2 pre7=2, p r e 8 = 4 pre_8=4 pre8=4。
-
当扫描到位置 i i i的时候,我们便只需要更新区间 [ p r e i + 1 , i ] [pre_i+1,i] [prei+1,i]就可以保证相同的数只被统计了一次!
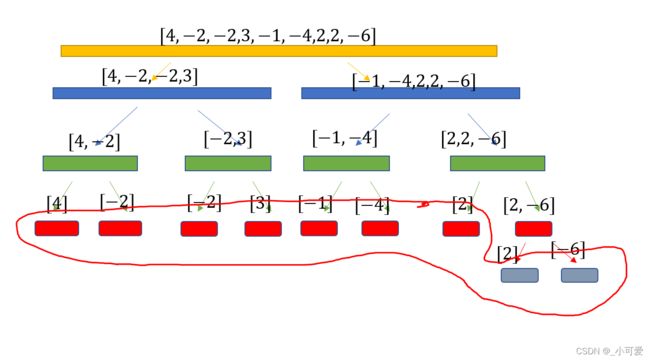
线段树部分:(我们还是用第一个序列作为例子。)
1、定义线段树的树结点:
struct Node {
ll sum, hismax, tag, hismaxtag; // 全部的值默认为 0
} tree[N<<2];
线段树建成后,其中的叶子结点(红圈包围的)的 s u m , h i s m a x , h i s m a x t a g , t a g sum, hismax, hismaxtag, tag sum,hismax,hismaxtag,tag与之前讨论的含义相同。而区间表示的含义则有些许不同:
- s u m sum sum:表示区间中最大的 s u m i sum_i sumi。
- h i s m a x hismax hismax:表示区间最大的 h i s m a x i hismax_i hismaxi,实质为区间最大的子段和。。
- t a g tag tag:对于区间所有的 t a g i tag_i tagi都要增加的子段和。
- h i s m a x t a g hismaxtag hismaxtag:表示 t a g tag tag出现过的最大的值,也就是最大的增加子段和。
现在询问两个区间:(已按照右端点大小排过序,排序的作用就是使得可以通过线性扫描一边更新,一边查询区间的的最大子段和): [ 1 , 2 ] 和 [ 1 , 5 ] [1, 2]和[1, 5] [1,2]和[1,5]。
2、预处理 p r e pre pre数组
for(int i = 1; i <= n; i++) {
cin >> val[i];
pre[i] = pos[val[i] + 100000]; // 因为值是有负数的,为了保证位置大于等于0,所以做了偏移处理
pos[val[i] + 100000] = i;
}
3、更新线段树
线段树向上区间合并:
inline void pushup(ll rt) {
// 根据上面的定义可以得到
tree[rt].sum = max(tree[ls].sum, tree[rs].sum);
tree[rt].hismax = max(tree[ls].hismax, tree[rs].hismax);
}
线段树向下压标记,进行”懒操作“,懒操作的意义在于,比如我要更新一段区间,但是里面所有的元素都要更新,那么我就设置一个 t a g tag tag来表示加上的子段,称作”增加“子段和。注意向下懒操作更新数据的顺序不能反!
inline void pushdown(ll rt) {
// 现在的子段和加上更新的最大”增加”子段和
tree[ls].hismax = max(tree[ls].hismax, tree[ls].sum + tree[rt].hismaxtag);
tree[rs].hismax = max(tree[rs].hismax, tree[rs].sum + tree[rt].hismaxtag);
// 现在的”增加“子段和加上更新的最大”增加”子段和
tree[ls].hismaxtag = max(tree[ls].hismaxtag, tree[ls].tag + tree[rt].hismaxtag);
tree[rs].hismaxtag = max(tree[rs].hismaxtag, tree[rs].tag + tree[rt].hismaxtag);
// 现在的子段和加上更新的“增加”子段和
// 现在的”增加“子段和加上更新的“增加“子段和
tree[ls].sum += tree[rt].tag;
tree[rs].sum += tree[rt].tag;
tree[ls].tag += tree[rt].tag;
tree[rs].tag += tree[rt].tag;
// 撤销标记
tree[rt].tag = tree[rt].hismaxtag = 0;
}
更新函数:
void update(ll rt, ll l, ll r, ll L, ll R, ll v) {
if(L <= l && r <= R) { // 懒操作
tree[rt].tag += v;
tree[rt].sum += v;
tree[rt].hismaxtag = max(tree[rt].hismaxtag, tree[rt].tag);
tree[rt].hismax = max(tree[rt].hismax, tree[rt].sum);
return;
}
pushdown(rt);
if(R <= mid) update(lson, L, R, v);
else if(L > mid) update(rson, L, R, v);
else {
update(lson, L, mid, v);
update(rson, mid+1, R, v);
}
pushup(rt);
}
查询函数:
ll query(ll rt, ll l, ll r, ll L, ll R) {
if(L <= l && r <= R) {
return tree[rt].hismax;
}
pushdown(rt);
if(R <= mid) return query(lson, L, R);
else if(L > mid) return query(rson, L, R);
else return max(query(lson, L, mid), query(rson, mid+1, R));
}
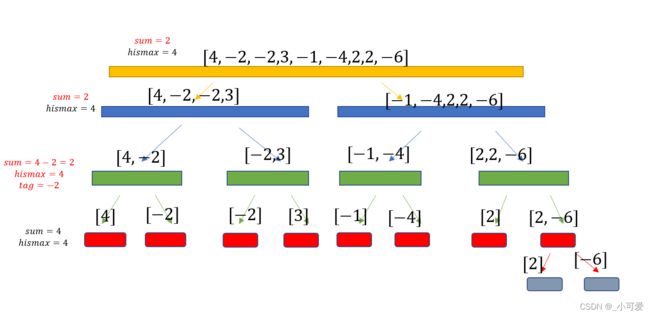
图解过程
加入第一个元素 4 4 4
u p d a t e ( l e f t = 1 , r i g h t = 1 ) update(left=1,right=1) update(left=1,right=1)

加入第二个元素 − 2 -2 −2
u p d a t e ( l e f t = 1 , r i g h t = 2 ) update(left=1,right=2) update(left=1,right=2)
q u e r y ( l e f t = 1 , r i g h t = 2 ) query(left=1, right=2) query(left=1,right=2)
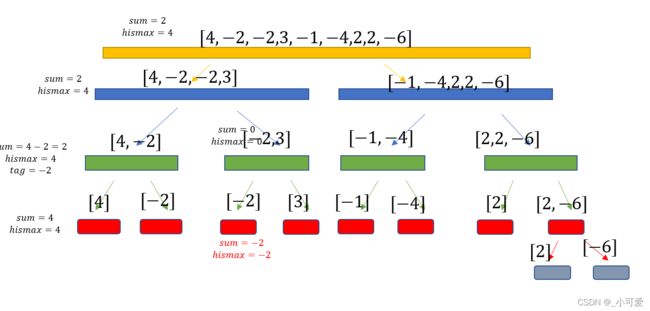
加入第三个元素 − 2 -2 −2
u p d a t e ( l e f t = 3 , r i g h t = 3 ) update(left=3,right=3) update(left=3,right=3)
加入第四个元素 3 3 3
u p d a t e ( l e f t = 1 , r i g h t = 4 ) update(left=1,right=4) update(left=1,right=4)
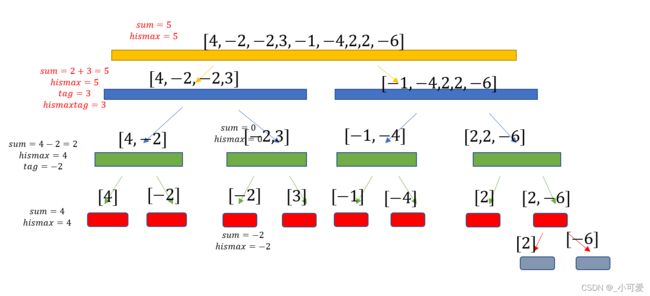
u p d a t e ( l e f t = 1 , r i g h t = 5 ) update(left=1,right=5) update(left=1,right=5)
查询区间 [ 1 , 5 ] [1,5] [1,5],得到结果 5 5 5
q u e r y ( l e f t = 1 , r i g h t = 5 ) query(left=1,right=5) query(left=1,right=5)
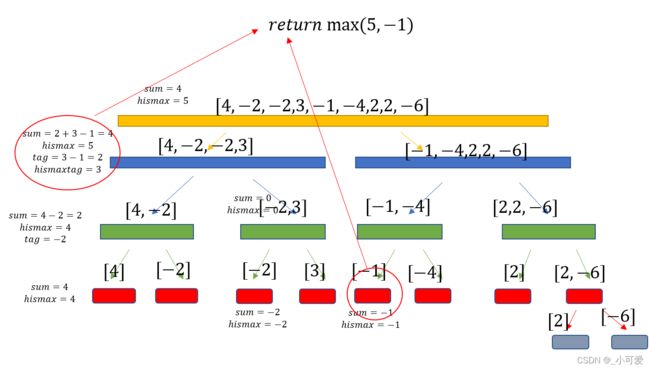
A C C o d e \color{Green}{AC} \, \color{Red}{Code} ACCode
#include 文章制作不易,转载请注明出处。