C. Game On Leaves（博弈论）

一、问题

二、分析

这道题简单来说，就是给我们一棵树，以及一个特殊点，每一次我们能够删除一个叶子节点，Ayush先手，谁能够最终删除这个特殊的节点，谁就是赢家。

这个特殊点记作：$X$

我们最终一定是到下图的情况时判断输赢：

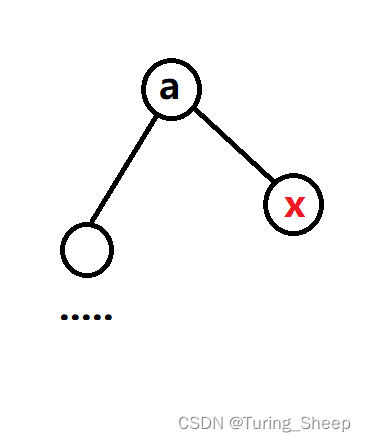
当我们的$x$出度为0的时候，此时轮到谁出手，谁就是赢家。

我们以下的讨论先排除$x$的子节点个数是0的情况。

case1:$x$是祖宗节点

我们先考虑一下简单的情况，我们假设$x$就是祖宗节点：那么我们必须删除除了$x$外的（所有点 - 1）个点，才能删除$x$。此时，我们只需要关注一下$x$下面的子节点个数。如果，

当前$x$的子节点个数是奇数，那么先手赢，如果当前$x$的子节点是偶数，则先手必输。

case2:$x$不是祖宗节点

接着，我们考虑$x$不是祖宗节点的条件下输赢的情况，我们还是分两类。

（1）$x$的子节点是偶数

如果此时$x$的子节点是偶数。

在这种条件下我们刚刚的结论其实还是成立的。如果其中一个人是先手，而此时$x$的子节点是偶数，此时先手必输，但是我们可以不删除$x$的子节点，而是删除其他的子节点，这样就把先手必输的状态转移给了对方。

那么同理对方也可以采取同样的方式将先手必输的状态再次转移，这样循环往复，直到整棵树中只剩下以$x$为根的子树。

那么此时，如果除了$x$的子树外（包括$x$），剩余的节点的数量如果是偶数的话，其实最后二者转移来转移去，一开始谁是先手必输，最后还是谁先手必输。
如果这些节点的数量是奇数的话，那么一开始的先手必输状态，在最后就i转变成了先手必赢的状态。

简单的来讲，在$x$的子树(包括$x$)的子节点个数是偶数的时候，如果其他节点的数目是奇数，则先手必赢，如果其他节点的数目是偶数的话，则先手必输。

所以，此时我们需要考虑的是其余节点的奇偶性。

（2）$x$的子节点是奇数

如果此时$x$的节点数是奇数。

在这种条件下， 先手处于必赢状态，此时我们一定是从$x$的子树中减去一个，然后让对手处于先手必败的状态，然后再重复刚刚的过程。

如果我们将除了$x$的子树（包括$x$）的点外的其余点的个数记录为$nums$的话，我们就需要讨论的是$nums+1$的奇偶性。

如果这个式子是奇数，则先手必赢，如果这个式子是偶数则先手必输。

那么无论x的子节点是奇还是偶，我们可以用一个式子表达出来，我们判断的是$nums+!siz(x)\%2$的奇偶性。如果这个式子是偶数，先手必赢，如果这个式子是奇数，先手必输。

接着，我们考虑一下，这两种$case$能否融合在一起？

如果我们把$case1$的情况套入$case2$中，此时这个式子中的$nums$就是0，按照$case1$中的结论，如果是奇数，就是必输，放到$case2$中，奇数取反变成$0$，按照$case2$偶数必输。发现二者得出的结论是一样的。

因此，我们就只需要利用这一个式子：$nums+!siz(x)\%2$的奇偶性， 即可判断。这个式子是奇数，先手必输，这个式子是偶数，先手必赢。

但是写到这里，我们发现这道题是一个无根树，所以我们很难去统计，因此，我们看看上述的这个表达式能否化简。

首先我们发现$siz(x)+nums=n-1$，因为$siz(x)$指的是不包括$x$的子节点，$nums$指的是其他点，所以相当于没算$x$，即$n-1$。

那么如果$n-1$是偶数的话，要么这两部分都是偶数，要么这两部分都是奇数。

如果这两部分都是偶数的话，刚才的式子就是奇数，如果两个式子都是奇数的话，刚才的式子还是奇数。
如果$n-1$是奇数的话，那么只能是奇数+偶数，如果左边部分是奇数，右边部分是偶数，这个式子就是偶数，如果左边部分是偶数，右边部分是奇数，这个式子还是偶数。

因此，如果$n-1$是偶数，这个式子就是奇数，先手必输。
如果$n-1$是奇数，这个式子就是偶数，先手必赢。

但是！有一种特殊情况，如果$x$的度小于等于1的时候，不管这个式子的奇偶性是什么，都是先手必赢。

三、代码

#include
#define endl '\n'
#define INF 0x3f3f3f3f
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N = 1e3 + 10;

void solve()
{
	int n,x;
	cin >> n >> x;
	int dex = 0;
	for(int i = 0; i < n - 1; i ++ )
	{
		int a, b;
		cin >> a >> b;
		if(a == x || b == x)
			dex ++;		
	}
	if(dex <= 1)
	{
		cout << "Ayush" << endl;
		return;
	}

	if((n - 1) % 2)
	{
		cout << "Ayush" << endl;
	}
	else
	{
		cout << "Ashish" << endl;
	}
	return;

}

int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	int t;
	cin >> t;
	while(t -- )
	solve();
}