凸包---（简单概念）

这里先介绍点概念（一般是点集覆盖问题）
输入各个点的坐标
 1. 将各点排序（必须的） ，为保证形成圈，把 P0 在次放在点表的尾 部； 2. 准备堆栈：建立堆栈 S，栈指针设为t，将0、1、2 三个点压入堆栈 S； 3. 对于下一个点 i 只要 S[t-1]、S[t]、i不做左转 就反复退栈； 将 i压入堆栈 S 4.堆栈中的点即为所求凸包； 其核心用 C 语言表示，仅仅是下面一段： t=-1; s[++t]=0; s[++t]=1; s[++t]=2; for (i=3;i<n;i++) { while (!left(s[t-1],s[t],i)) t--; s[++t]=i; } 下面我们来看一个例子： 这是排序后的几个点

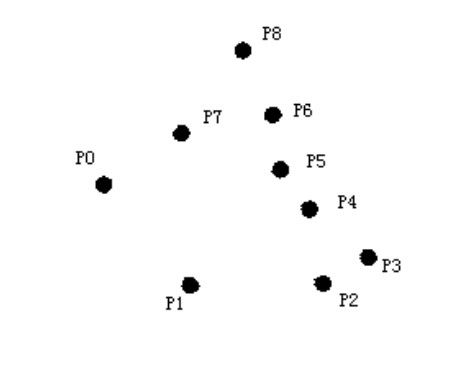
准备堆栈（有线段相连的点表示在栈中的点） 栈内元素：P0,P1,P2

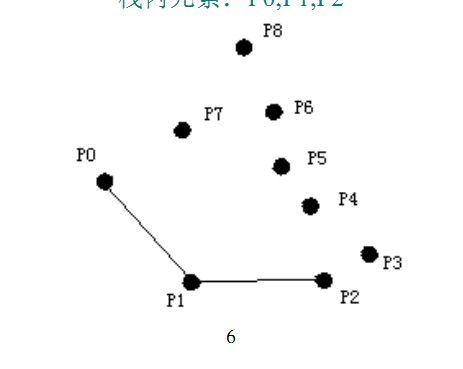
 考虑 P3：P1,P2,P3呈左转，P3入栈 栈内元素：P0,P1,P2,P3

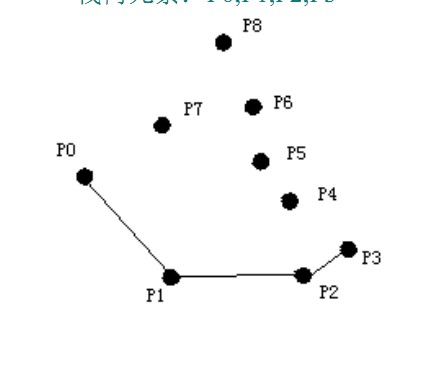
 考虑 P4：P2,P3,P4呈左转，P4入栈 栈内元素：P0,P1,P2,P3,P4

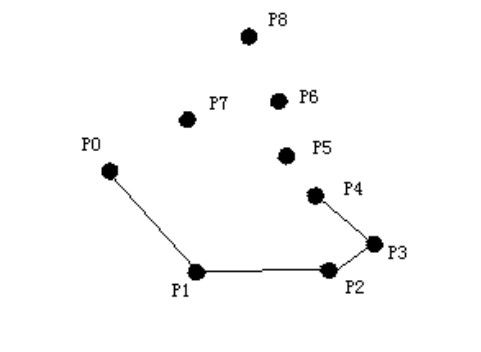
 考虑 P5：P3,P4,P5非左转，退栈 栈内元素：P0,P1,P2,P38

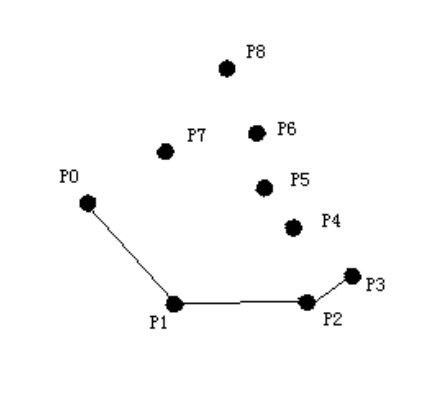
 现在，P2,P3,P5 呈左转，P5入栈 栈内元素：P0,P1,P2,P3,P5

（此时情况如图，算法舍弃了 P4）

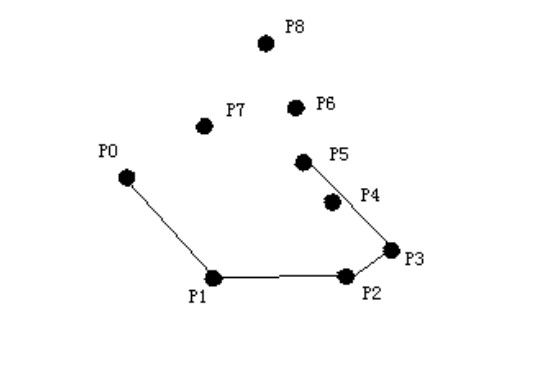
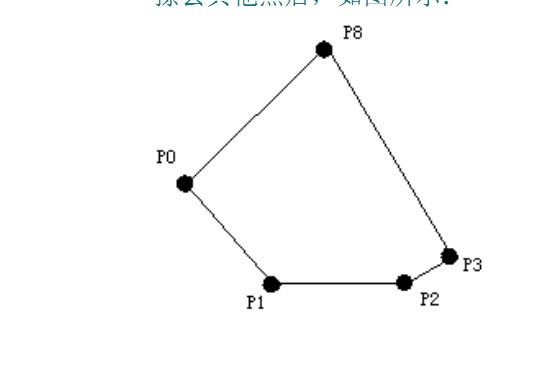
 以此方法进行下去，直到所有点都被考虑过 最终的栈中元素为 P0,P1,P2,P3,P8,P0，正是所求凸包 擦去其他点后，如图所示：

 

这里只是些简单概念，至于具体的，结合问题在具体讨论~~~