AtCoder ABC276 A~F

https://atcoder.jp/contests/abc276
1500pts(ABCDE), rank 1126.

A - Rightmost

下标从1开始，所以最后的答案要+1.
所以我一开始写了这么一个代码：

	cin >> s;
	ans = -1;
	for (int i = 0; i < s.size(); ++i) {
		if (s[i] == 'a') ans = i;
	}
	cout << ans + 1;

没测样例直接交，WA。
原因是ans初始化为-1，当无解时，输出ans+1=0.
应当把ans初始化为-2.

B - Adjacency List

Adjacency List，邻接表。
图的存储。

int n, m;
vector<int> g[MAXN];
 
int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr); cout.tie(nullptr);
	
	cin >> n >> m;
	for (int i = 1; i <= m; ++i) {
		int a, b; cin >> a >> b;
		g[a].push_back(b); g[b].push_back(a);
	}
	
	for (int i = 1; i <= n; ++i) {
		cout << g[i].size() << ' ';
		sort(g[i].begin(), g[i].end());
		for (int j = 0; j < g[i].size(); ++j) {
			cout << g[i][j] << ' ';
		}
		cout << "\n";
	}
	
	return 0;
}

C - Previous Permutation

STL - CE

一开始，想起来STL里有个next_permutation，那是不是也有prev_permutation？
在本机上打了一下，编译出错。只好放弃这个想法了。

分析 - WA

观察样例：9 8 6 5 10 3 1 2 4 7的前一个是9 8 6 5 10 2 7 4 3 1。
有以下发现：

• 只有开头的9 8 6 5 10没有变化。
• 结尾的1 2 4 7递增，只考虑这几个数，这就是字典序最小的排列，没有上一个。所以它们带上了上一个数3，这样3 1 2 4 7不递增，有上一个。这就导致了上一点：开头五个数不变。

问题转化为求3 1 2 4 7这样，整个不递增，除了第一个数就递增的上一个排列。
答案是2 7 4 3 1，可以猜到，把第一个数换成比它小的最大数，其他的数递减排列在后面。

不难证明这个算法的正确性，却WA了，下文会分析它错在哪。

int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr); cout.tie(nullptr);
	
	cin >> n;
	for (int i = 1; i <= n; ++i) {
		cin >> a[i];
	}
	
	//找到“前面的数不变”的位置，样例中的3
	int pos = n;
	b.push_back(a[n]);
	for (int i = n - 1; i; --i) {
		pos = i;
		b.push_back(a[i]);
		if (a[i] > a[i + 1]) break;
	}
	
	//输出
	sort(b.begin(), b.end(), greater<int>());
	for (int i = 1; i <= pos - 1; ++i) {
		cout << a[i] << ' ';
	}
	cout << a[pos] - 1 << ' ';
	for (int i = 0; i < b.size(); ++i) {
		if (b[i] != a[pos] - 1) cout << b[i] << ' ';
	} cout << "\n";
	
	return 0;
}

STL - AC

上面的代码短时间内大抵修不好了，再试试prev_permutation。

？

编译怎么过了，难道是当时拼错单词了？
不管了，这题A了。

分析 - AC（赛后）

刚刚的代码错在这：

cout << a[pos] - 1 << ' ';
for (int i = 0; i < b.size(); ++i) {
	if (b[i] != a[pos] - 1) cout << b[i] << ' ';
} cout << "\n";

a[pos]-1想表示的是，结尾递增序列中比a[pos]小的最大数，可是a[pos]-1不一定在递增序列中。
改一改，就过了。

int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr); cout.tie(nullptr);
	
	cin >> n;
	for (int i = 1; i <= n; ++i) {
		cin >> a[i];
	}
	
	//j:上面的pos
	//k:新的开头
	int j = n - 1;
	b.push_back(a[n]);
	while (a[j + 1] > a[j]) {
		b.push_back(a[j--]);
	} b.push_back(a[j]);
	int k = lower_bound(a + j + 1, a + n + 1, a[j]) - a - 1;
	
	sort(b.begin(), b.end(), greater<int>());
	for (int i = 1; i <= j - 1; ++i) {
		cout << a[i] << ' ';
	}
	cout << a[k] << ' ';
	for (int i = 0; i < b.size(); ++i) {
		if (b[i] != a[k]) cout << b[i] << ' ';
	} cout << "\n";
	
	return 0;
}

D - Divide by 2 or 3

统计每个数2和3的因子个数，分别取最小值。每个数2和3的因子个数分别减去这个最小值，全部加起来，结果算出来。
无解情况：去除每个数的所有2和3因子后，结果不同。
简单，不讲。
好像也可以用gcd做。事实上，取最小值就像是gcd。

int n, a[MAXN], d2[MAXN], d3[MAXN], x, y, ans;
 
int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr); cout.tie(nullptr);
	
	cin >> n;
	for (int i = 1; i <= n; ++i) {
		cin >> a[i];
		while (!(a[i] % 2)) a[i] /= 2, ++d2[i];
		while (!(a[i] % 3)) a[i] /= 3, ++d3[i];
	}
	
	for (int i = 2; i <= n; ++i) {
		if (a[i] != a[1]) {
			cout << -1 << "\n";
			return 0;
		}
	}
	
	x = INF, y = INF;
	for (int i = 1; i <= n; ++i) {
		ckmin(x, d2[i]); ckmin(y, d3[i]);
	}
	
	for (int i  = 1; i <= n; ++i) {
		ans += d2[i] - x + d3[i] - y;
	}
	cout << ans << "\n";
	
	return 0;
}

E - Round Trip

dfs - AC

从S，走到相邻的上下左右，四个起点。

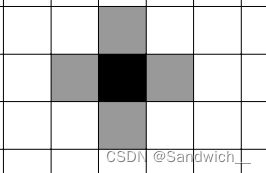
S出，S入，考虑从一个起点开始，另一个起点结束，此时已经有三个点了。只要再有一个点——从不同的起点，不经过S和障碍，能走到同一个点——就找到了符合条件的路径。
换言之，只要有两个起点之间是连通的（不经过S）。
连通块问题，从四个起点分别dfs，如果某个点被标记了多次，输出Yes。

int h, w, ox, oy;
vector<vector<bool> > g, vis;
vector<vector<int> > cnt;
 
void dfs(int x, int y) {
	vis[x][y] = true;
	++cnt[x][y];
	for (int i = 0; i < 4; ++i) {
		int nx = x + DIR[i][0], ny = y + DIR[i][1];
		if (!vis[nx][ny] && !g[nx][ny]) { 
			dfs(nx, ny);
		}
	}
}
 
int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr); cout.tie(nullptr);
	
	cin >> h >> w;
	g.resize(h + 2);
	for (int i = 0; i <= w + 1; ++i) {
		g[0].push_back(true); g[h + 1].push_back(true);
	}
	for (int i = 1; i <= h; ++i) {
		g[i].resize(w + 2);
		g[i][0] = g[i][w + 1] = true;
		for (int j = 1; j <= w; ++j) {
			char ch; cin >> ch;
			if (ch == 'S') ox = i, oy = j;
			if (ch == '.') g[i][j] = false;
			else g[i][j] = true;
		}
	}
	
	vis.resize(h + 2); cnt.resize(h + 2);
	for (int i = 0; i <= h + 1; ++i) {
		for (int j = 0; j <= w + 1; ++j) {
			vis[i].push_back(false); cnt[i].push_back(0);
		}
	}
	
	for (int i = 0; i < 4; ++i) {
		int x = ox + DIR[i][0], y = oy + DIR[i][1];
		if (!g[x][y]) {
			for (int j = 1; j <= h; ++j) {
				for (int k = 1; k <= w; ++k) {
					vis[j][k] = false;
				}
			}
			dfs(x, y);
		}
	}
	
	for (int i = 1; i <= h; ++i) {
		for (int j = 1; j <= w; ++j) {
			if (cnt[i][j] > 1) {
				cout << "Yes\n";
				return 0;
			}
		}
	}
	cout << "No\n";
	
	return 0;
}

优化判断 - AC（赛后）

上文判断有没有某一个点，从不同的起点能达到。
简单地，判断从某一个起点，能不能到达另一个起点。
体现在代码中，从某一个起点dfs，到达了多于1个起点（那一个是它自己）。

int h, w, ox, oy, res;
vector<vector<bool> > g, vis;
 
void dfs(int x, int y) {
	vis[x][y] = true;
	if (abs(x - ox) + abs(y - oy) == 1) ++res;//这里
	for (int i = 0; i < 4; ++i) {
		int nx = x + DIR[i][0], ny = y + DIR[i][1];
		if (!vis[nx][ny] && !g[nx][ny]) { 
			dfs(nx, ny);
		}
	}
}
 
int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr); cout.tie(nullptr);
	
	cin >> h >> w;
	g.resize(h + 2);
	for (int i = 0; i <= w + 1; ++i) {
		g[0].push_back(true); g[h + 1].push_back(true);
	}
	for (int i = 1; i <= h; ++i) {
		g[i].resize(w + 2);
		g[i][0] = g[i][w + 1] = true;
		for (int j = 1; j <= w; ++j) {
			char ch; cin >> ch;
			if (ch == 'S') ox = i, oy = j;
			if (ch == '.') g[i][j] = false;
			else g[i][j] = true;
		}
	}
	
	vis.resize(h + 2);
	for (int i = 0; i <= h + 1; ++i) {
		for (int j = 0; j <= w + 1; ++j) {
			vis[i].push_back(false);
		}
	}
	
	for (int i = 0; i < 4; ++i) {
		int x = ox + DIR[i][0], y = oy + DIR[i][1];
		res = 0;//本次dfs经过的起点个数
		if (!g[x][y]) {
			for (int j = 1; j <= h; ++j) {
				for (int k = 1; k <= w; ++k) {
					vis[j][k] = false;
				}
			}
			dfs(x, y);
			if (res > 1) {
				cout << "Yes\n";
				return 0;
			}
		}
	}
	cout << "No\n";
	
	return 0;
}

关于vector（补）

$4\le H\times W\le 10^6$，所以我使用了vector >。
事实上，仔细一想就会发现，用vector g[1000005]也不会爆空间，而且更好写。
这题本应10min左右写完，但是我花了20min，用了很多时间调试那个两维vector，关于到底用reserve还是resize。

并查集 - AC（补）

连通块问题，也可以用并查集解决。
看有没有两个起点在同一个连通块。

int h, w, ox, oy, fa[MAXH];
vector<bool> g[MAXH];
 
int ind(int x, int y) {
	return (x - 1) * w + y;//我曾写成x*(h-1)+y
}
 
int find(int x) {
	return fa[x] == x ? x : fa[x] = find(fa[x]);
}
void merge(int x, int y) {
	fa[find(x)] = find(y);
}
 
int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr); cout.tie(nullptr);
	
	cin >> h >> w;
	for (int i = 0; i <= w + 1; ++i) {
		g[0].push_back(true); g[h + 1].push_back(true);
	}
	for (int i = 1; i <= h; ++i) {
		g[i].push_back(true);
		for (int j = 1; j <= w; ++j) {
			char ch; cin >> ch;
			if (ch == 'S') ox = i, oy = j;
			g[i].push_back(ch != '.');
		}
		g[i].push_back(true);
	}
	
	for (int i = 1; i <= h; ++i) {
		for (int j = 1; j <= w; ++j) {
			fa[ind(i, j)] = ind(i, j);
			if (!g[i][j]) {
				if (!g[i - 1][j]) merge(ind(i, j), ind(i - 1, j));
				if (!g[i][j - 1]) merge(ind(i, j), ind(i, j - 1));
			}
		}
	}
	
	//只有四个起点，所以用了暴力的两层枚举
	//也可以统计四个起点所在的连通块个数
	for (int i = 0; i < 4; ++i) {
		int x1 = ox + DIR[i][0], y1 = oy + DIR[i][1];
		for (int j = i + 1; j < 4; ++j) {
			int x2 = ox + DIR[j][0], y2 = oy + DIR[j][1];
			if (!g[x1][y1] && !g[x2][y2] && find(ind(x1, y1)) == find(ind(x2, y2))) {
				cout << "Yes\n";
				return 0;
			}
		}
	}
	cout << "No\n";
	
	return 0;
}

F - Double Chance

暴力 - WA

当时想着先拿暴力分，顺便看看算法正确性。

k的答案是
$$\frac{1}{k^2}\sum _{i=1}^k\sum _{j=1}^{k}max\{a[i],a[j]\}$$
k等于1到n都要解，显然要看看怎么从k-1的答案推到k。
简单，先忽略$1/k^2$，新的答案是$ans+2{\sum }_{i=1}^{k-1}max\{a[i],a[k]\}$.
每次输出$k^2$的逆元乘$ans$.
这样就可以写暴力了。

可是WA，奇怪。

int n;
ll a[MAXN], ans;
 
ll gcd(ll a, ll b) {
	return !(a % b) ? b : gcd(b, a % b);
}
void exgcd(ll a, ll b, ll &x, ll &y) {
	if (!b) {
		x = 1; y = 0;
		return;
	}
	exgcd(b, a % b, x, y);
	ll t = x;
	x = y; y = t - y * a / b;
}
 
int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr); cout.tie(nullptr);
	
	cin >> n;
	for (int i = 1; i <= n; ++i) {
		cin >> a[i];
	}
	
	for (int i = 1; i <= n; ++i) {
		for (int j = 1; j < i; ++j) {
			plusmod(ans, max(a[i], a[j]) * 2);
		}
		plusmod(ans, a[i]);
		ll x = ans, y = (ll)i * i, inv, tmp;
		exgcd(y, MOD, inv, tmp); inv = mod(inv);
		cout << mod(x * inv) << "\n";
	}
	
	return 0;
}

暴力 - TLE（赛后）

赛后查标程发现，exgcd中应该是y = t - a / b * y;而非y = t - y * a / b;
比赛时，单独拿出十分钟多先单独调exgcd，WA后又调了整个程序很久。
算上之前，exgcd写错已经至少三次了，但是每次都没记住。所以赛后查漏补缺很重要。

树状数组 - AC（赛后）

$ans+2{\sum }_{i=1}^{k-1}max\{a[i],a[k]\}$
比如a中前面的几个数是$12356$，新加入一个$4$，ans就会加上2倍的$4+4+4+5+6$和$4$.
a[k]把小于等于它的数全部变成它。容易想到树状数组。

算法很简单，代码5min左右就能写完（在暴力的基础上）。要是exgcd一次写对，比赛时就能A掉这题了罢（悲）。

int n;
ll a[MAXN], ans, t[MAXA], cnt[MAXA];
 
void exgcd(ll a, ll b, ll &x, ll &y) {
	if (!b) {
		x = 1; y = 0;
		return;
	}
	exgcd(b, a % b, x, y);
	ll t = x;
	x = y; y = t - a / b * y;
}
 
int lowbit(int x) { return x & -x; }
void modify(ll *t, int pos, ll v) {
	for (int i = pos; i < MAXA; i += lowbit(i)) {
		t[i] += v;
	}
}
ll getsum(ll *t, int pos) {
	ll res = 0;
	for (int i = pos; i; i -= lowbit(i)) {
		res += t[i];
	}
	return res;
}
 
int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr); cout.tie(nullptr);
	
	cin >> n;
	for (int i = 1; i <= n; ++i) {
		cin >> a[i];
	}
	
	for (int i = 1; i <= n; ++i) {
		plusmod(ans, 2 * (getsum(cnt, a[i]) * a[i] + getsum(t, MAXA - 1) - getsum(t, a[i])));
		plusmod(ans, a[i]);
		
		ll x = ans, y = (ll)i * i, inv, tmp;
		exgcd(y, MOD, inv, tmp); inv = mod(inv);
		cout << mod(x * inv) << "\n";
		
		modify(t, a[i], a[i]);
		modify(cnt, a[i], 1);
	}
	
	return 0;
}

G - Count Sequences

还没仔细看，我再想想。