P1443 马的遍历（BFS）

题目描述
有一个 n \times mn×m 的棋盘，在某个点 (x, y)(x,y) 上有一个马，要求你计算出马到达棋盘上任意一个点最少要走几步。

输入格式
输入只有一行四个整数，分别为 n, m, x, yn,m,x,y。

输出格式
一个n×m 的矩阵，代表马到达某个点最少要走几步（左对齐，宽 55 格，不能到达则输出 -1−1）。
输入输出样例
输入
3 3 1 1
输出
0 3 2
3 -1 1
2 1 4
对于全部的测试点，保证

思路分析：
此题需要理解BFS，BFS模板

queue<> q;
q.push(初始状态)；
while(!q.empty()){
//记录下来队列中的队首元素的结点
	a=q.front();
	q.pop();
	//寻找队列中每一个结点对应的各种情况
	for(枚举a中的所有合法可达状态v){
		if(本状态合法){
			执行标记操作;
			q.push(v);//将新的情况放入队列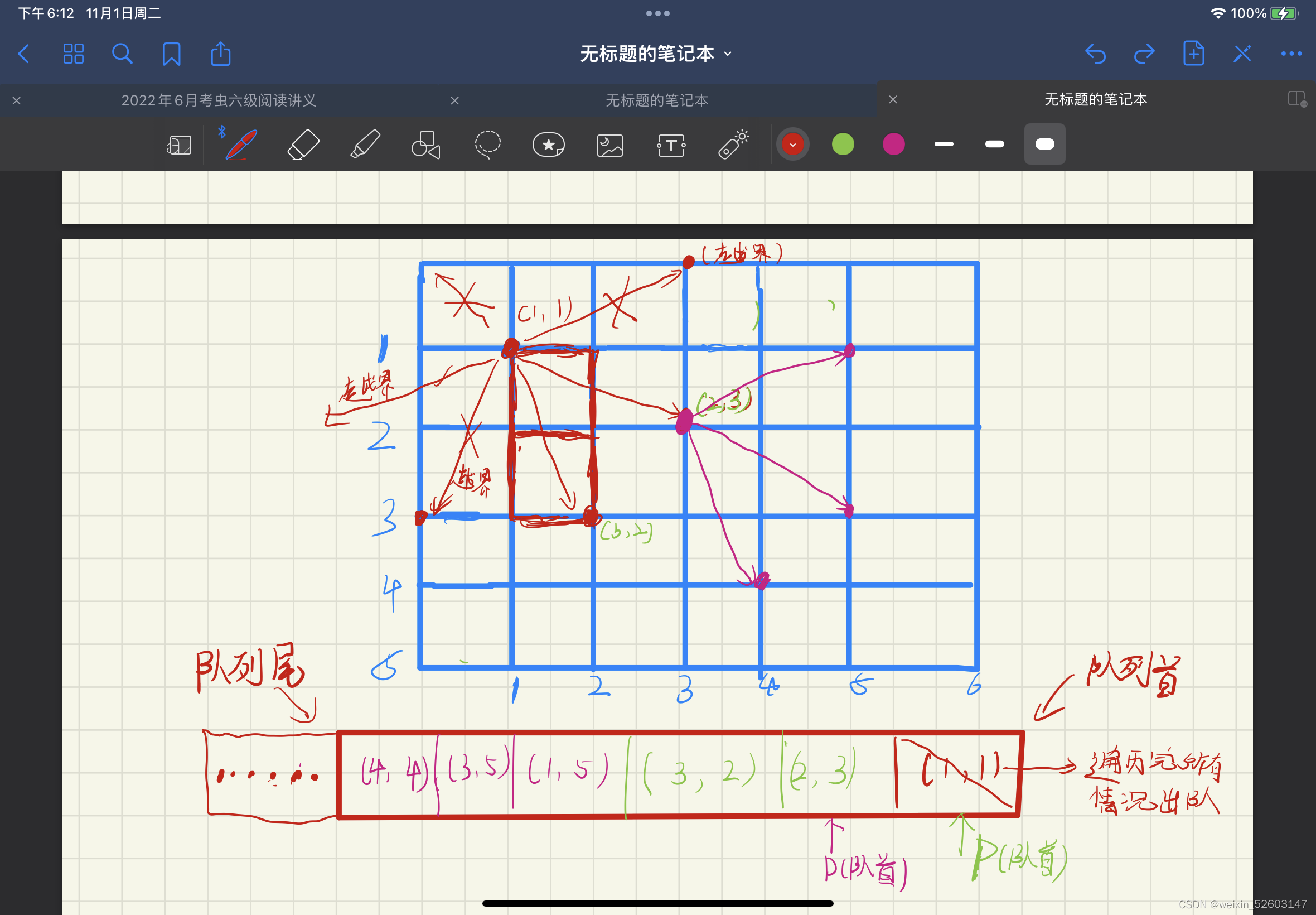![请添加图片描述](https://img-blog.csdnimg.cn/c8d564f37858487b80eeac90887a4cfd.png)

		}
	}
}

该题使用宽度搜索BFS，遍历从某一点开始 通过规则了解马走日，所以马的走法一共有八种利用dxx[]与dyy[]记录下马的行走方案。
利用BFS从起点添加进队列，并标记v[]为true，防止重复走过。利用两个队列记录起始结点入队，遍历起始节点所有走过的八种情况，符合条件的将a[][]数组该点的值进行更换 a[xx][yy]=a[q1.peek()][q2.peek()]+1; ；
并将该点入队，随后标记该点已经访问。
当八种情况全部遍历判断后，队列中的队首元素所有能走的情况已经入队，所以该结点已经无用，利用poll()，出队操作。
队列的特点：先入先出

Java题解

import java.util.*;
public class Main {
    static int n,m;
    static int bx,by;
    static int sum=0;
    static int dxx[]=new int[]{1,2,-1,-2,-2,-1,1,2};
    static int dyy[]=new int[]{2,1,2,1,-1,-2,-2,-1};
    static int [][]a=new int[410][410];
    static boolean [][]v=new boolean[410][410];
    public static void main(String[] args) {
        Scanner sc=new Scanner(System.in);
         n = sc.nextInt();
         m=sc.nextInt();
         bx=sc.nextInt();
         by=sc.nextInt();
        for(int i=1;i<=n;i++){
            Arrays.fill(a[i],-1);
        }
        bfs();
        for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
                System.out.printf("%-5d",a[i][j]);
            }
            System.out.println();
        }
    }
  public static void bfs(){
        int i;
        Queue<Integer> q1=new LinkedList<>();
        Queue<Integer> q2=new LinkedList<>();
        q1.offer(bx);
        q2.offer(by);
        a[bx][by]=0;
        v[bx][by]=true;
        while(!q1.isEmpty()){
        for( i=1;i<=8;i++){
           int xx=q1.peek()+dxx[i-1];
           int yy=q2.peek()+dyy[i-1];
           if(xx>0&&xx<=n&&yy>0&&yy<=m&&!v[xx][yy]){
               a[xx][yy]=a[q1.peek()][q2.peek()]+1;
               q1.offer(xx);
               q2.offer(yy);
               v[xx][yy]=true;
           }
        }
        q1.poll();
        q2.poll();
     }
   }
}

c++题解

#include
using namespace std;
int n,m,x,y;
int hor[405][405];//存储矩阵
bool vis[405][405];//标记是否访问过
int dx[]={1,2,-1,-2,-2,-1,1,2};
int dy[]={2,1,2,1,-1,-2,-2,-1};
//广度搜索
void bfs(){
	queue<int> x1;
	queue<int> y1;
	//将马的初始位置放入队列中
	x1.push(x);
	y1.push(y);
	//队列不是空
	while(!x1.empty()){
		//马走日，类似走迷宫，定义位置偏移量
		//寻找能走的方向
		for(int i=0;i<8;i++){
			//走日字型
			int xx=x1.front()+dx[i];
			int yy=y1.front()+dy[i];
			//判断这个新的状态是否合法,不超越矩阵的边界
			//之前没有访问过
			if(xx>=1&&xx<=n&&yy>=1&&yy<=m&&!vis[xx][yy]){
				//满足条件，访问该点
				//标记该点已经访问过
				vis[xx][yy]=true;
				hor[xx][yy]=hor[x1.front()][y1.front()]+1;
				x1.push(xx);
				y1.push(yy);
			}	
		}
		//遍历完一个点的所有情况后从这一个点到别的方向已经没有路可走
		//这个点已经不可以走了所有这个点可以出队列
		x1.pop();
		y1.pop();
	}
}
int main(){
	//输入n,m的矩阵x,y为吗的起始位置
	cin>>n>>m>>x>>y;
	memset(hor,-1,sizeof(hor));//标记初始化hor数组为-1
	//设置马的初始位置为0
	hor[x][y]=0;
	vis[x][y]=true;
	bfs();
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			printf("%-5d",hor[i][j]);
		}
		cout<<endl;
	}
}