论文笔记：Revisiting Single Image Depth Estimation: Toward Higher Resolution Maps with ...(WACV2019)
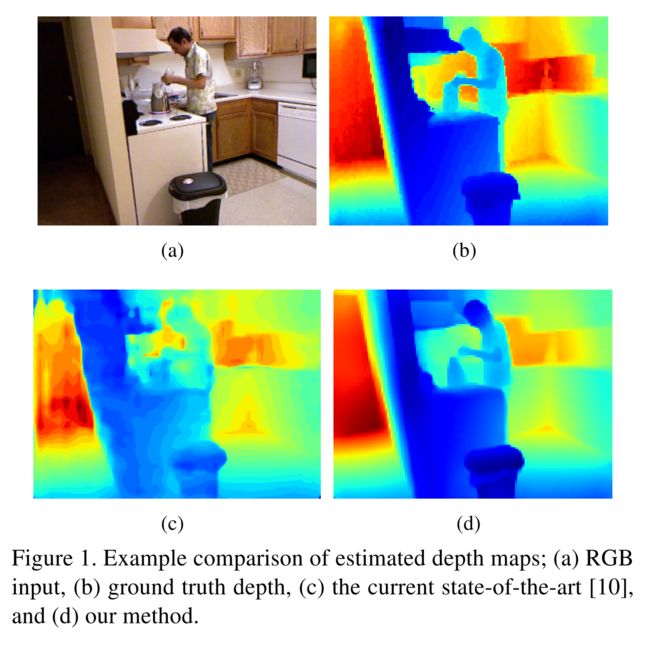
以往方法往往深度预测损失了分辨率或者在边界存在扭曲和模糊问题。
本文提出2个改进：1. 不同尺度下提取特征的策略 2. 使用3个损失，分别是深度、梯度、法向量
c：当前最好模型，存在物体形状扭曲、小物体缺失、马赛克
Introduction
早期：
比如Eigen提出的，直接cnn预测，分辨率很低
目前：
上投影(up-projection)上采样方法
CRF结合CNN，端到端学习
联合多任务学习
近期：
扩张卷积(dilated convolution)
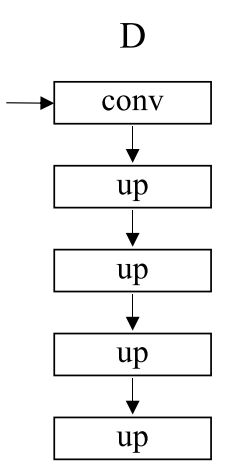
本文模型结构：4个模块：E:encoder和D:decoder，类似skip connections效果的MMF(a multi-scale feature fusion (MFF) module to fuse features of different resolutions extracted by E)，最后3层卷积细化的R。
本文损失：尖锐的不连续点通常出现在场景中物体的遮挡边界处，在深度图中形成阶跃边缘。这种结构是(自然场景)深度图的一个关键属性。如上所述，然而，以前的方法往往不能正确恢复这些边缘。
Related Work
Skip connections:
经典结构，比如U-Net，对称插入在decoder和encoder的对应层之间，并且通道数要一样
本文直接合并encoder各层的上采样特征图，也就MMF的任务。
Gradient-based loss:
值得思考问题：RGBD足够先进可用，基于dl的深度估计的价值？
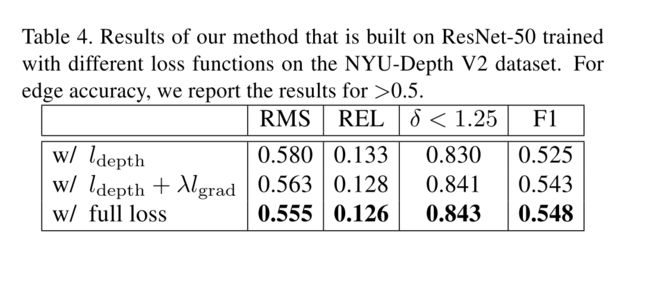
本文3个损失： l depth l_{\text {depth}} ldepth、 l grad l_{\text {grad}} lgrad、 l normal l_{\text {normal}} lnormal能够互补共同改进性能。
Proposed Method
Improved Network Design
输入图片：228 x 304 * 3
E: 编码器encoder
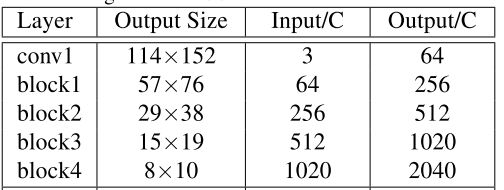
conv1： 1/2
block1： 1/4
block2： 1/8
block3： 1/16
block4： 1/32
D:解码器decoder
conv1： 1/32
up1： 1/16
up2： 1/8
up3： 1/4
up4： 1/2
所以这里是尺寸不变，通道数减半(2040 -> 1020)
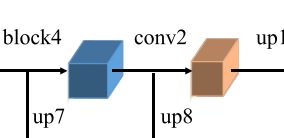
MFF:多尺度融合模块multi-scale feature fusion module
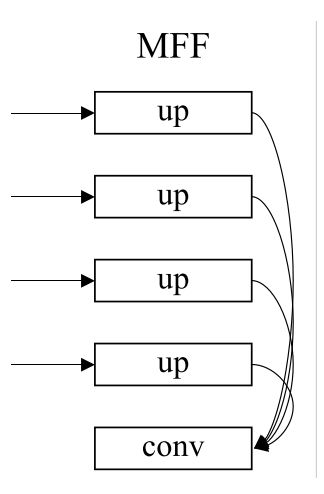
up5：1/2 (接block1输出：57 x 76 ，上投影通道配对16层，上采样 x2，输出 114 x 152)
up6：1/2 (接block2输出：29 x 38 ，上投影通道配对16层，上采样 x4，输出 114 x 152)
up7：1/2 (接block3输出：15 x 19 ，上投影通道配对16层，上采样 x8，输出 114 x 152)
up8：1/2 (接block4输出：8 x 10 ，上投影通道配对16层，上采样 x16，输出 114 x 152)
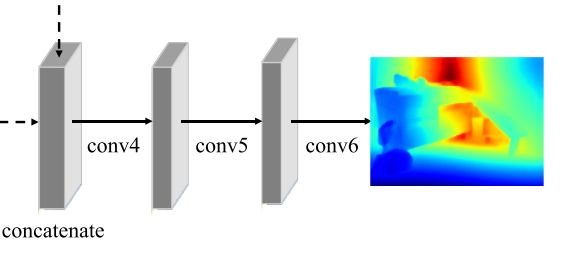
conv3：1/2 (输入：up5 + up6 + up7 + up8 = 64层(concatenate) 输出 64层)
R:细化模块refinement module
conv4：1/2（输入：MMF：64 + D：up4 64 = 128层(concatenate)）
conv5：1/2
conv6：1/2
网络最终输出：114 x 152 x 1 ，是输入分辨率的1半，1通道深度图
对于不同层的特征图抽样：
可以看到，浅层(底层)的特征具有更多细节，深层(顶层)的特征细节更少但是具有更全局的特征。
损失函数
深度预测的loss常用的就是l1损失
l 1 = 1 n ∑ i = 1 n e i l_{1}=\frac{1}{n} \sum_{i=1}^{n} e_{i} l1=n1i=1∑nei
其中， e i = ∥ d i − g i ∥ 1 e_{i}=\left\|d_{i}-g_{i}\right\|_{1} ei=∥di−gi∥1
除此之外还有l2损失和Huber损失
l2:
l 1 = 1 n ∑ i = 1 n e i 2 l_{1}=\frac{1}{n} \sum_{i=1}^{n} e_{i}^2 l1=n1i=1∑nei2
Huber: L δ ( e i ) = { 1 2 e i 2 for ∣ e i ∣ ≤ δ δ ( ∣ e i ∣ − 1 2 δ ) , otherwise L_{\delta}(e_{i})=\left\{\begin{array}{ll} \frac{1}{2} e_{i}^{2} & \text { for }|e_{i}| \leq \delta \\ \delta\left(|e_{i}|-\frac{1}{2} \delta\right), & \text { otherwise } \end{array}\right. Lδ(ei)={21ei2δ(∣ei∣−21δ), for ∣ei∣≤δ otherwise
作者希望深度误差太大时，不要对应的产生这样的loss，所以对于太远的误差，经过log变换会变小。算一种处理离群点的方式
所以使用一个log变换：
l d e p t h = 1 n ∑ i = 1 n F ( e i ) l_{\mathrm{depth}}=\frac{1}{n} \sum_{i=1}^{n} F\left(e_{i}\right) ldepth=n1i=1∑nF(ei)
其中， F ( x ) = ln ( x + α ) F(x)=\ln (x+\alpha) F(x)=ln(x+α)， α ( > 0 ) \alpha(>0) α(>0)为超参数。
但是 l d e p t h l_{\mathrm{depth}} ldepth只能对深度误差的变化比较敏感，对于边缘误差的变化不敏感。在深度方向 z z z上对于边缘的误差还是当做深度误差处理。即当深度误差大时，并不能直接反映边缘误差大。所以提出使用 l g r a d l_{\mathrm{grad}} lgrad来互补实现对边缘误差的变化的敏感。
l g r a d = 1 n ∑ i = 1 n ( F ( ∇ x ( e i ) ) + F ( ∇ y ( e i ) ) ) l_{\mathrm{grad}}=\frac{1}{n} \sum_{i=1}^{n}\left(F\left(\nabla_{x}\left(e_{i}\right)\right)+F\left(\nabla_{y}\left(e_{i}\right)\right)\right) lgrad=n1i=1∑n(F(∇x(ei))+F(∇y(ei)))
下面举例说明 e i , d i , g i e_{i}, d_{i}, g_{i} ei,di,gi的梯度关系：
∣ ∇ x ( d i ) − ∇ x ( g i ) ∣ = ∣ [ d ( x + 1 , y ) − d ( x , y ) ] − [ g ( x + 1 , y ) − g ( x , y ) ] ∣ = ∣ [ d ( x + 1 , y ) − g ( x + 1 , y ) ] − [ d ( x , y ) − g ( x , y ) ] ∣ = ∣ e ( x + 1 , y ) − e ( x , y ) ∣ = ∇ x ( e i ) |\nabla_{x}\left(d_{i}\right) - \nabla_{x}\left(g_{i}\right)|\\ =|[d(x+1, y)-d(x, y)] - [g(x+1, y)-g(x, y)]|\\ =|[d(x+1, y)-g(x+1, y)] - [d(x, y)-g(x, y)]|\\ =|e(x+1, y) - e(x, y)|\\ =\nabla_{x}\left(e_{i}\right)\\ ∣∇x(di)−∇x(gi)∣=∣[d(x+1,y)−d(x,y)]−[g(x+1,y)−g(x,y)]∣=∣[d(x+1,y)−g(x+1,y)]−[d(x,y)−g(x,y)]∣=∣e(x+1,y)−e(x,y)∣=∇x(ei)
上式只是为了说明 l g r a d l_{\mathrm{grad}} lgrad表示的预测深度图和真实深度图各种图像的梯度之差可以在 e e e上计算， e = ∣ d − g ∣ e = |d-g| e=∣d−g∣， e e e就是由 e i e_i ei组成的map。
所以 ∇ x ( e i ) \nabla_{x}\left(e_{i}\right) ∇x(ei)表示在第 i i i个像素对应 e i e_{i} ei的 x x x方向梯度，同理可得 y y y方向。梯度可以使用Priwitt、Sobel算子在 e i e_{i} ei的map上计算。
此外，对于表面只有细微变化的情况， l g r a d l_{\mathrm{grad}} lgrad也不会太敏感。所以提出表面的法向量误差：
l normal = 1 n ∑ i = 1 n ( 1 − ⟨ n i d , n i g ⟩ ⟨ n i d , n i d ⟩ ⟨ n i g , n i g ⟩ ) l_{\text {normal }}=\frac{1}{n} \sum_{i=1}^{n}\left(1-\frac{\left\langle n_{i}^{d}, n_{i}^{g}\right\rangle}{\sqrt{\left\langle n_{i}^{d}, n_{i}^{d}\right\rangle} \sqrt{\left\langle n_{i}^{g}, n_{i}^{g}\right\rangle}}\right) lnormal =n1i=1∑n⎝⎛1−⟨nid,nid⟩⟨nig,nig⟩⟨nid,nig⟩⎠⎞
其中，法向量定义： n i d ≡ [ − ∇ x ( d i ) , − ∇ y ( d i ) , 1 ] ⊤ n_{i}^{d} \equiv\left[-\nabla_{x}\left(d_{i}\right),-\nabla_{y}\left(d_{i}\right), 1\right]^{\top} nid≡[−∇x(di),−∇y(di),1]⊤， n i g ≡ [ − ∇ x ( g i ) , − ∇ y ( g i ) , 1 ] ⊤ n_{i}^{g} \equiv\left[-\nabla_{x}\left(g_{i}\right),-\nabla_{y}\left(g_{i}\right), 1\right]^{\top} nig≡[−∇x(gi),−∇y(gi),1]⊤，即法向量垂直于x和y梯度方向。 ⟨ ⋅ , ⋅ ⟩ \langle\cdot, \cdot\rangle ⟨⋅,⋅⟩表示向量内积，即用内积表示夹角大小情况。
横轴表示x(水平方向)，纵轴表示z(深度方向)
第一行：深度误差的变化，只有 l d e p t h l_{depth} ldepth敏感
第二行：边缘误差的变化，深度对于边缘的误差还是当做深度误差处理。所以需要使用 l g r a d l_{grad} lgrad，用梯度来计算误差
第三行：细微的边缘误差的变化， l g r a d l_{grad} lgrad也不会很敏感，所以使用 l n o r m a l l_{normal} lnormal来计算法向量的夹角误差。
最终loss的定义：
L = l depth + λ l grad + μ l normal L=l_{\text {depth }}+\lambda l_{\text {grad }}+\mu l_{\text {normal }} L=ldepth +λlgrad +μlnormal
Accuracy Measures for Depth Estimation
均方根误差Root mean squared error (RMS)：
1 T ∑ i = 1 T ( d i − g i ) 2 \sqrt{\frac{1}{T} \sum_{i=1}^{T}\left(d_{i}-g_{i}\right)^{2}} T1i=1∑T(di−gi)2
平均相对误差Mean relative error (REL): 1
1 T ∑ i = 1 T ∥ d i − g i ∥ 1 g i \frac{1}{T} \sum_{i=1}^{T} \frac{\left\|d_{i}-g_{i}\right\|_{1}}{g_{i}} T1i=1∑Tgi∥di−gi∥1
Mean log 10 error (log 10)：
1 T ∑ i = 1 T ∥ log 10 d i − log 10 g i ∥ 1 \frac{1}{T} \sum_{i=1}^{T}\left\|\log _{10} d_{i}-\log _{10} g_{i}\right\|_{1} T1i=1∑T∥log10di−log10gi∥1
Thresholded accuracy：
max ( d i g i , g i d i ) = δ < threshold \max \left(\frac{d_{i}}{g_{i}}, \frac{g_{i}}{d_{i}}\right)=\delta<\text { threshold } max(gidi,digi)=δ< threshold
取值为， d i d_{i} di的百分比
此外，为了评估边缘准确度，提出下面评估方法：
f x ( i ) 2 + f y ( i ) 2 > t h r e s h o l d \sqrt{f_{x}(i)^{2}+f_{y}(i)^{2}}>threshold fx(i)2+fy(i)2>threshold
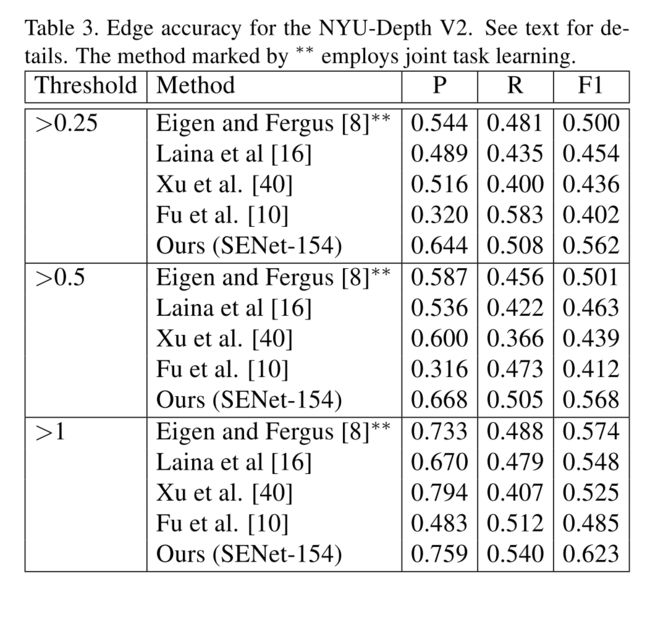
其中， f x f_{x} fx and f y f_{y} fy为3 x 3的Sobel算子。所以当上式大于给定阈值0.25、0.5、1时，则认为第 i i i个像素为边界，上述操作在预测输出的depth map上。如果此时真实depth map为边界。则设为ture，以此计算precision §, recall ® and F1 score。
Experiments
定量实验：
边缘准确度：
定性实验：
消融研究：
所以额外的2个损失对提示准确度有帮助。
Conclusion
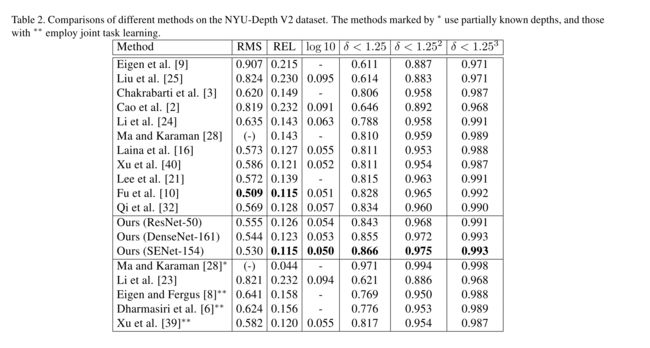
一是网络架构的改进设计，它由编码器、解码器、多尺度特征融合模块和细化模块四个模块组成。编码器可以使用任何基础网络，如ResNet、DenseNet和SENet。整个网络以端到端方式训练，没有任何后期处理细化
二是损失函数改进， l g r a d l_{\mathrm{grad}} lgrad对于提示对于边缘的敏感性， l normal l_{\text {normal }} lnormal 对于微小的误差敏感