光流方法总结一

之前实习时接触过一段时间光流，本意是想用于辅助跟踪的。由于siammask框架自带分割功能，因此用稠密光流也是能跟踪的，虽然最终没用上。。就像光线暗时，2个黑衣人并列走着，距离太远，人显得太小。。最终试了几种光流都不能跟好。

都是整理之前记录的笔记留下的，之前是边看边记录的。。对光流理解还比较浅，可能有些地方理解不对。。

传统方法：

OpenCV相关API： Link
光流法假设前提：

1. 同一目标在相邻帧之间的亮度恒定
2. 相邻帧之间物体的运动微小，即短距离运动

基本约束方程：
根据假设前提1，亮度恒定可得公式
$$I(x,y,t)=I(x+dx,y+dy,t+dt)\text{\hspace{1em}(1)}$$
其中$dx，dy$为目标移动距离。
将式（1）的右侧泰勒展开得式(2)（因为约束2，运动微小，故一阶泰勒展开可以近似？）
$$I(x,y,t)=I(x,y,t)+\frac{\partial I}{\partial x}dx+\frac{\partial I}{\partial y}dy+\frac{\partial I}{\partial t}dt+ϵ\text{\hspace{1em}(2)}$$
略去2阶无穷小项和约掉$I(x,y,t)$。且2边除以$dt$得
$$\frac{\partial I}{\partial x}\frac{dx}{dt}+\frac{\partial I}{\partial y}\frac{dy}{dt}+\frac{\partial I}{\partial t}\frac{dt}{dt}=0\text{\hspace{1em}(3)}$$
令$I_x=\frac{\partial I}{\partial x},I_y=\frac{\partial I}{\partial y},I_t=\frac{\partial I}{\partial t}$为图像灰度在3个方向上的偏导数，
令$u=\frac{dx}{dt}，v=\frac{dy}{dt}$为所求光流矢量。
则得到约束方程：
$$I_{x}u+I_{y}v+I_t=0\text{\hspace{1em}(4)}$$

（记：只看最终的约束方程，$I_x,I_y$为原始帧灰度值在x,y方向的变化率，$I_t$的约束感觉很弱，光流矢量仅靠原始帧的差分去求？）

LK光流（Lucas–Kanade）
相对原始的光流假设前提，LK光流新增一个假设前提
3.“空间一致”的假设，即所有的相邻像素有相似的行动。也即在目标像素周围m×m的区域内，每个像素均拥有相同的光流矢量。

即若取3x3的区域，则可得9个约束方程。因为“空间一致”的假设，9个方程里只有2个变量，即9个约束方程仅有2个未知数。由最小2乘法求解光流矢量。
相关链接：https://www.cnblogs.com/riddick/p/10586662.html
(即相当于邻域内的点都做同样的平移运动，对旋转失效)

图像金字塔引入：
构建多层图像金字塔，同时在每层金字塔保持在mxm区域内计算光流。
a.孔径问题：光流法只关注小范围时，可能存在孔径问题。
具体可以参考：https://blog.csdn.net/hankai1024/article/details/23433157
图像金字塔可以缓解。

b.因为原始光流是建立在小运动的假设上的，即只考虑一个小邻域内。而实际情况中存在较大的运动。图像金字塔也可缓解“大运动”现象。

Lucas-Kanade改进算法
稀疏光流算法，即加入图像金字塔的LK算法（不过其求解是由亮度差最小，即寻找使亮度差值最小的$dx,dy$。。感觉这还好理解点，基本约束方程里的求差分方式不好理解。）
(https://blog.csdn.net/qq_30815237/article/details/87208319）

Farneback算法：
稠密光流算法(https://www.jianshu.com/p/355caf1d38a3)，具体原理还没全理解(用2次多项式去拟合？)

深度学习方法

图源SelFlow:
评估指标EPE : 指所有像素点的gound truth和预测出来的光流之间差别距离（欧氏距离）的平均值

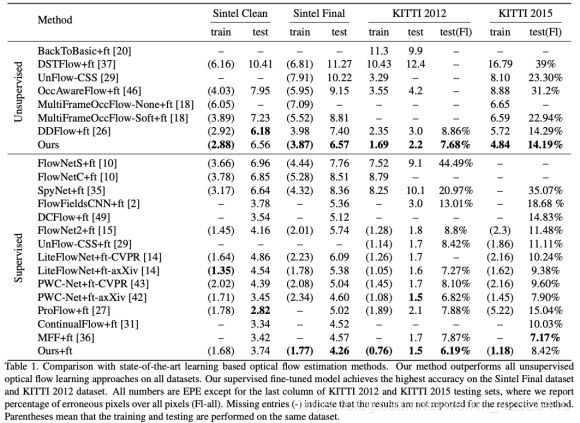
监督学习方法：

其数据基本为合成数据集。

FlowNet

论文：https://arxiv.org/pdf/1504.06852.pdf
代码：https://github.com/NVIDIA/flownet2-pytorch/tree/master/networks
所用数据集Flying Chairs为合成数据集
提出2种结构从深度学习引入光流
1.FlowNetSimple: 直接将2帧cat成6通道图，直接输入网络，由网络直接生成光流结果
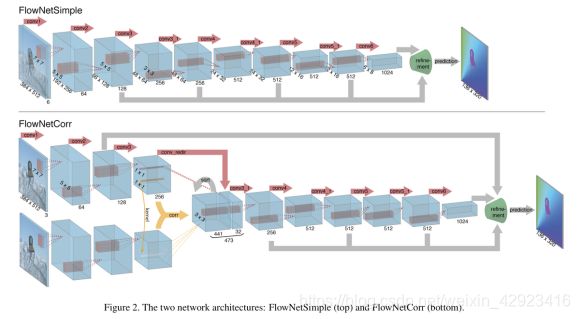
2.F lowNetCorr:2帧图片分别经过卷积后，将前帧当做 WH 个 11 的卷积核，对后帧做卷积操作。2帧特征图的大小一致，为降低计算量，每个卷积核只对后帧的（2K+1）邻域做卷积（论文中为21邻域），得到21211的特征图而后拉直成441。(公式中 f1(x1+o) 是否应该改为 f1(x) ? )

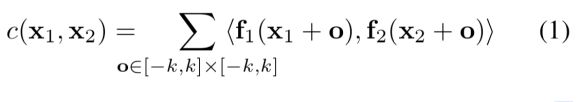
FlowNet2.0

论文：https://arxiv.org/pdf/1612.01925.pdf
代码：https://github.com/NVIDIA/flownet2-pytorch
相对FlowNet，增加数据集，改变训练策略，堆叠网络结构

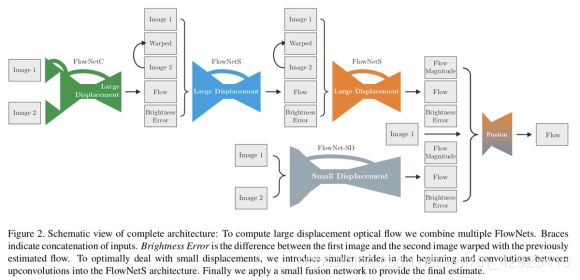
堆叠网络：
第一个网络输入为2帧image。

其后的网络输入：

• Flow：光流输出结果
• warped：Image2按前一个网络输出的Flow warp得到
• Brightness Error：warped与Image1的绝对差值。
• FlowNet-SD：针对小位移，去掉一个下采样，改小卷积核
  (注：Warp: 即image2根据光流得到对应像素在image1中的坐标，然后做类似index_select操作 （nn.functional.grid_sample)）

PWC-Net:

论文：http://openaccess.thecvf.com/content_cvpr_2018/papers/Sun_PWC-Net_CNNs_for_CVPR_2018_paper.pdf
代码：https://github.com/NVlabs/PWC-Net
一些实现：https://zhuanlan.zhihu.com/p/67302545

网络结构：

左为图像金字塔，右为实际使用的feature pyr。即加入FPN逐层细化

• Cost volume layer：FlowNet中的corr操作，多了个均值？Third, as the cost volume is a more discriminative representation of the optical flow than raw images。
• Optical flow estimator：一系列卷积操作
• Context network：好像就是继续堆网络，加dilate？

warp和cost volumn操作：https://zhuanlan.zhihu.com/p/67302545

Warp: 即image2根据光流得到对应像素在image1中的坐标，然后做类似index_select操作 （nn.functional.grid_sample）。因此运动⽐较⼤时，warp图可能出现2个⽬标（运动部分坐标加上光流，不运动部分坐标不变， 所以可能存在2个位置对应image1的同⼀个坐标）

cost volumn：
主要为一种向量相乘求均值（点乘），就是一种求相关性的操作（因为理想情况下image2经过warp后应该与image1一致（在运动对象位置处）），基本和FlowNetC中的corr操作一样。

原始PWC-Net的Correlation为C扩展，要求torch=0.2其torch.utils.ffi.create_extension的接口在新版已不能用。用pytorch重写Correlation层。运行后与源码demo基本一致。(stride1=1，不好改。corr_multiply不知道干什么用。刚好论文中的设置stride=1，corr_multiply=1)

class Correlation(nn.Module):
	def __init__(self, pad_size=0, kernel_size=1, max_displacement=1, stride1=1, stride2=1, corr_multiply=1): 
		super(Correlation, self).__init__() 
		self.pad_size = pad_size 
		self.kernel_size = kernel_size 
		self.max_displacement = max_displacement 
		self.stride1 = stride1 
		self.stride2 = stride2 
		self.corr_multiply = corr_multiply 
		print("pad_size=%d, kernel_size=%d, max_displacement=%d, stride1=%d, stride2=%d, corr_multiply=%d"%( 
			pad_size, kernel_size, max_displacement, stride1, stride2, corr_multiply 
			)) 
	
	def forward(self, i1, i2): 
		#assert i1.shape[1] == i2.shape[1]: 
		size_ = i1.size() 
		d = self.max_displacement * 2 + 1 
		[n, c, h, w] = size_
		i2 = F.unfold(i2, (d, d), padding=self.pad_size, stride=self.stride2) 
		i2 = i2.view(i2.size(0), c, d, d, -1).permute(0,4,2,3,1) 
		i1 = i1.permute(0,2,3,1).contiguous().view(n, -1, 1, 1, c) 
		out = torch.mean(i1 * i2, dim = (4)) 
		out = out.permute(0,2,3,1).contiguous().view(n, d * d, h, w) 
		#print(" corr cost :", time.time() - stime)
		return out # * self.corr_multiply

上图为源码中给出结果，下图为pytorch版correlation结果。并不完全一致。不确定是代码问题还是其他问题(不知道demo中的结果是不是pytorch实现的，GitHub上有注明pytorch版本效果会差点)。

MFF：A Fusion Approach for Multi-Frame Optical Flow Estimation

论⽂：https://arxiv.org/abs/1810.10066
代码：https://github.com/NVlabs/PWC-Net/tree/master/Multi_Frame_Flow

其输⼊为3帧，其中前2个PWC-Net去获取 t-1 --> t 的前向光流和 t --> t-1的反向光流。

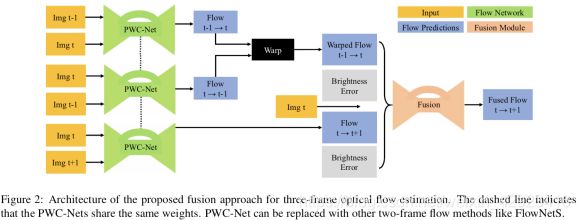
其中的Warp操作里，与FlowNet2.0和SelFlow的光流对image进行warp不同，而是光流对光流进行warp。感觉这种操作的效果会更优，因为要的结果就是光流信息。而对image warp感觉就是把运动对象copy-paste一份（没有重合部分），而如果多copy一份前帧到当前帧的光流，所提供的运动趋势应该能更好的帮助去获取从当前帧到下一帧的光流。（warp操作，FlowNwt2为对image操作，LiteFlowNet对feature操作，MFF对光流操作）

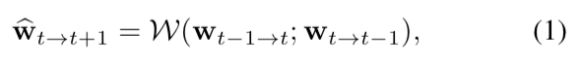
2个Brightness Error定义如下。公式2中的$\hat{w}$为公式1中定义。公式3中的w(不戴帽)为结构图中第三个PWC-Net的输出结果。