暴力递归转动态规划（十）

题目
给定一个二维数组matrix[][]，一个人必须从左上角出发，最终到达右下角，沿途只可以向下或者向右走，沿途的数字都累加就是距离累加和。返回最小距离累加和。
这道题中会采用压缩数组的算法来进行优化

暴力递归
暴力递归方法的整体思路是根据小人所在的位置（当前值），通过向下传递（向左走向右走）来获取最终选择路径的最小值。
所以base case可以确定：

1. 如果小人走到了最后一行，那么接下来就只能向下走。
2. 如果小人走到了最后一列，那么接下来就只能向左走。
3. 如果小人走到了matrix[][]的最后一个格子，返回当前值给上层做处理，取最小值。
4. 否则，既可以向左也走可以向右走，并获取最小值。

所以暴力递归的方法就出来了。

public static int minPathSum1(int[][] matrix) {

        if (null == matrix || matrix.length == 0 || matrix[0] == null || matrix[0].length == 0) {
            return -1;
        }

        int row = matrix.length;
        int col = matrix[0].length;

        return process(row - 1, col - 1, 0, 0, matrix);
    }

    //返回 matrix[i...][j....] 位置的最小值。
    public static int process(int row, int col, int curRow, int curCol, int[][] matrix) {
        //当走到最后一个位置，返回matrix中最后一个位置的值
        if (curRow == row && curCol == col) {
            return matrix[row][col];
        }
        //走到最后一行，只能往右走，只能向右累加
        if (curRow == row) {
            return matrix[curRow][curCol] + process(row, col, curRow, curCol + 1, matrix);
        }

        //走到最后一列，只能向下走
        if (curCol == col) {
            return matrix[curRow][curCol] + process(row, col, curRow + 1, curCol, matrix);
        }

        //否则，可以向右走，可以向下走，进行累加。
        int curValue = matrix[curRow][curCol];

        int p1 = curValue + process(row, col, curRow + 1, curCol, matrix);

        int p2 = curValue + process(row, col, curRow, curCol + 1, matrix);

        return Math.min(p1, p2);
    }

动态规划
这道题的动态规划也不难，给定的是一个二维数组matrix[][]，每次行和列会进行变化（可变参数）,所以可以创建一个和matrix大小相等的dp[][]来存放每一步计算的值。
因为只可以向下走或向右走，所以dp中任选一个格子的依赖是依赖自己的左侧的值和上面的值。其中dp中第一行的值只会依赖同行左侧的值，dp中第一列的值只会依赖同一列上面的值。
所以先将dp中第一行和第一列的值填充好后，其余的按照依赖关系填充，即可完善dp表。

代码

 public static int dp(int[][] matrix) {
        if (null == matrix || matrix.length == 0 || matrix[0] == null || matrix[0].length == 0) {
            return -1;
        }

        int row = matrix.length;
        int col = matrix[0].length;
        int[][] dp = new int[row][col];

        dp[0][0] = matrix[0][0];
        for (int i = 1; i < col; i++) {
            dp[0][i] = dp[0][i - 1] + matrix[0][i];
        }

        for (int j = 1; j < row; j++) {
            dp[j][0] = dp[j - 1][0] + matrix[j][0];
        }

        for (int i = 1; i < row; i++) {
            for (int j = 1; j < col; j++) {
                dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + matrix[i][j];
            }
        }
        return dp[row - 1][col - 1];
    }

优化
动态规划方法中是创建了一个和matrix[][]大小相等的dp表，通过填充dp表来完善的代码。

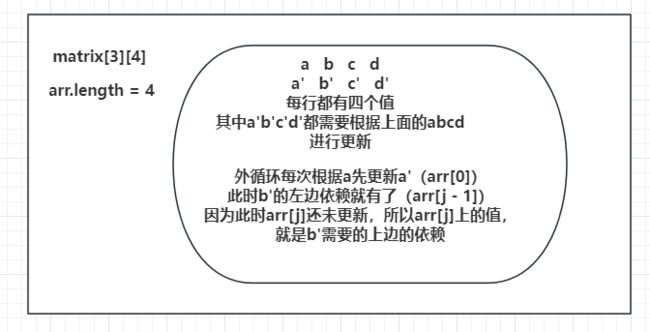
如果给定的matrix[][]太大了，是不是我的dp表也要跟着很大，并且，在填充dp表时，第三行依赖第二行的值，第四行依赖第三行的值，此时。第二行的值就已经没有用了，不再需要它了，所以是不是只需要一个跟matrix[][]中列的长度相等的一维数组arr[]就够了。

代码

 public static int minPathSum2(int[][] matrix) {
        if (matrix == null || matrix.length == 0 || matrix[0] == null || matrix[0].length == 0) {
            return 0;
        }
        int row = matrix.length;
        int col = matrix[0].length;
        int[] arr = new int[col];
        arr[0] = matrix[0][0];
		//根据matrix第一行的值填充arr
        for (int i = 1; i < col; i++) {
            arr[i] = arr[i - 1] + matrix[0][i];
        }
        
        for (int i = 1; i < row; i++) {
            arr[0] += matrix[i][0];
            for (int j = 1; j < col; j++) {
            //arr[j - 1] : 相当于我依赖的左边
            //arr[j]  : 因为此时arr[j]的值还没修改，还是上一行的值，相当于自己的上面。 
                arr[j] = Math.min(arr[j - 1], arr[j]) + matrix[i][j];
            }
        }
        return arr[col - 1];
    }