【常见缓存算法原理及其C++实现】LFU篇
一、缓存算法简介
（一）缓存算法应用背景
缓存的应用场景和范围十分广泛，下面给出其十分常见的两种应用背景：
首先，在操作系统内部，由于内存资源十分有限，而每个进程又都希望独享一块很大的内存空间。所以诞生了一种“虚拟内存”机制，它将进程的一部分内容暂留在磁盘中，在需要时再进行数据交换将其放入内存，这个过程就需要用到缓存算法机制进行置换。
其次，对于各类应用项目开发而言，在巨大的数据量面前，Cache 是不可或缺的。因为无论是针对本地端的浏览器缓存，还是针对服务器端的缓存(例如，redis 内存数据库缓存)，Cache 都是提高性能的最常用的一种方式。它不仅可以加速用户的访问，同时也可以降低服务器的负载和压力。
（二）常见缓存算法原理
1、FIFO（Fist In First Out）
先进先出，这是最简单、最公平的一种算法，它认为一个数据最早进入缓存，在将来该数据被访问的可能性最小。其原理是最早进入缓存的数据应该最早被淘汰掉，即当缓存空间被占满时，最先进入的数据会被最早被淘汰。
2、LRU（Least Recently Used）
最近最少使用，它的设计原则借鉴了时间局部性原理，该算法认为如果数据最近被访问过，那么将来被访问的几率也更高，反之亦然。其原理是将数据按照其被访问的时间形成一个有序序列，最久未被使用的数据应该最早被淘汰掉，即当缓存空间被占满时，缓存内最长时间未被使用的数据将被淘汰掉。
详细原理及C++实现可参考我的另一篇博客，应对面试这一篇就够了 LRU详解及C++实现
3、LFU（Least Frequently Used）
最不经常使用，它的设计原则使用了概率思想，该算法认为如果一个对象的被访问频率很低，那么再次被访问的概率也越低。其原理是缓存空间中被访问次数最少的数据应该最早被淘汰掉，即当缓存空间被占满时，缓存内被访问频率最少的数据将被置换走。
二、LFU 基本算法描述
建议不了解 LRU 的同学可以先参考我上节给出的另一篇详细讲解 LRU 的博客进行学习后，再来研究 LFU，不然理解本算法会有些难度
- 初始化一个大小为 n 的缓存空间，每个数据节点均有 key、value 和 freq（被访问频数）三个值；
- 当有新加入数据操作时，先判断该 key 值是否已经在缓存空间中，如果在的话更新 key 对应的 value 值，并将该数据访问频数加 1；
- 如果新加入数据的 key 值不在缓存空间中，则判断缓存空间是否已满，若缓存空间未满，则构造新的节点（访问频数为 1）加入到缓存空间，否则把该数据（访问频数为 1）加入到缓存空间的右边并淘汰掉访问频数最低且最久未被访问的数据（当访问频数最低的数据不止一个时，淘汰那个最久未被访问的数据）；
- 访问一个数据且该数据存在于缓存空间中，返回该数据对应值并将该数据访问频数加 1；
- 访问一个数据但该数据不存在于缓存空间中，返回 - 1 表示缓存中无该数据。
在实际应用场景中，我们依然希望上述所有操作的平均时间复杂度均可以控制在 O(1) 内，以保证缓存的高效运行，下面给出具体数据结构选择及实现。
三、LFU 算法实现
（一）LFU 算法主要函数及数据结构
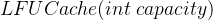：缓存空间初始化，以 正整数 capacity 作为容量初始化 LRU 缓存。
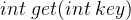：访问缓存数据，如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 ，对缓存数据每执行一次 get 操作，其访问频数就加 1。
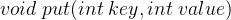：向缓存中加入数据，如果关键字 key 已经存在，则变更其数据值 value ，并将其访问频数加 1；如果不存在，则向缓存中插入该组 key-value，即该 key 首次加入缓存空间，设置其访问频数为 1 。如果插入操作导致关键字数量超过 capacity ，则应该逐出访问频数最低且最久未被访问的数据（当访问频数最低的数据不止一个时，淘汰那个最久未被访问的数据）。
算法实现过程中的难点依旧在于函数 get 和 put 必须以 O(1) 的平均时间复杂度运行，下面我们先来分析一下 LRU 与 LFU 二者的区别：
- LRU 是根据时间维度来选择将要淘汰的元素，即删除掉最长时间没被访问的元素。
- LFU 是根据频数和时间维度来选择将要淘汰的元素，即首选删除访问频数最低的元素。如果两个元素的访问频数相同，则淘汰最久没被访问的元素。
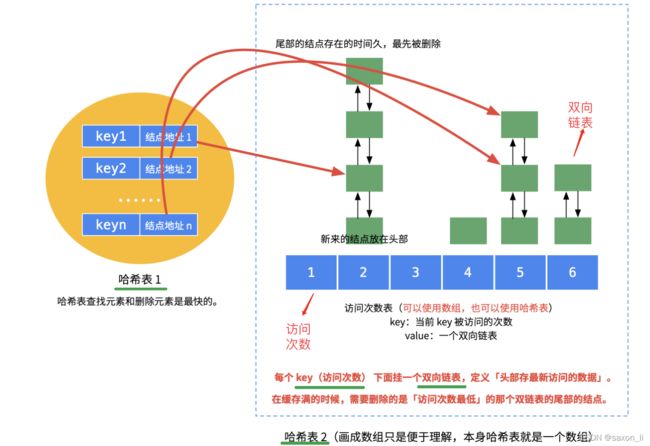
就是说LFU淘汰的时候会选择两个维度，先比较频数，选择访问频率最小的元素；如果频率相同，则按时间维度淘汰掉最久远的那个元素。LRU的实现是 1 个哈希表加上 1 个双链表，与LRU类似，想要完成上述条件，LFU 仍需要结合哈希表和双向链表这两个结构进行操作，不过需要用 2 个哈希表再加上 N 个双链表才能实现先按照频数再按照时间两个纬度的淘汰策略，具体 LFU 数据结构参考下图。
实现 LFU 用到了 2 个哈希表，分别用来记录 key - Node 及 freq - freqList 两种映射关系，下面对于这两个哈希表给出详细解释：
unordered_map hashNode;
unordered_map hashFreq; - 哈希表 1：hashNode，节点哈希表，用于快速获取数据中 key 对应的节点信息
- 哈希表 2：hashFreq，频数双向链表哈希表，为每个访问频数 freq 构造一个双向链表 freqList，并且用哈希表联系二者关系以快速定位
（二）LFU 算法代码
（1）首先，我们先来定义一下双向链表中的节点结构 Node
//双向链表节点
struct Node{
int key;
int value;
int freq;//为每个双向链表的节点增加 freq 值，用于记录其被访问频数
Node *pre,*next;
Node(int key,int value,int freq)
{
this->key=key;
this->value=value;
this->freq=freq;
pre=nullptr;
next=nullptr;
}
};（2）其次，定义一下双向链表的结构 hashFreq
//双向链表
struct FreqList{
int freq;//标识双向链表中节点的共同访问频数
Node *L,*R;
FreqList(int freq)//双向链表构造函数
{
this->freq=freq;
L=new Node(-1,-1,1);
R=new Node(-1,-1,1);
L->next=R;
R->pre=L;
}
};（3）再定义缓存容量 n、最小访问频数 minFreq、节点哈希表 hashNode 和频数双向链表哈希表 hashFreq
int n;//缓存空间大小
/*
整个缓存中的节点最小访问频数， LFU 中为每一个频数构造一个双向链表，
当缓存空间满了时，首先需要知道当前缓存中最小的频数是多少，再需要找到
该最小频数下最久未使用的数据淘汰。想要在 O(1) 时间复杂度下完成上述
操作，处理使用双向链表结构，还需要动态记录维护缓存空间中最小访问频数 minFreq
*/
int minFreq;
unordered_map hashNode;//节点哈希表，用于快速获取数据中 key 对应的节点信息
unordered_map hashFreq;//频数双向链表哈希表，为每个访问频数构造一个双向链表，并且用哈希表联系二者关系 其中 minFreq 是一个尤为关键的变量，它是整个缓存中的节点最小访问频数， LFU 中为每一个频数构造一个双向链表，当缓存空间满了时，首先需要知道当前缓存中最小的频数是多少，再需要找到该最小频数下最久未使用的数据淘汰。想要在 O(1) 时间复杂度下完成上述操作，处理使用双向链表结构，还需要动态记录维护缓存空间中最小访问频数 minFreq
（4）下面，来实现一下 LFU 缓存空间初始化函数
// LFU 缓存构造函数
LFUCache(int capacity) {
n=capacity;//初始化缓存空间
minFreq=0;//初始化最小访问频数为 0
}（5）再来实现一下访问缓存数据的 get 函数
//访问缓存数据
int get(int key) {
if(hashNode.find(key)!=hashNode.end())//缓存中存在该 key
{
Node *node=hashNode[key];//利用节点哈希表，O(1) 时间复杂度下定位到该节点
//每次 get 操作会将该节点访问频数 +1，所以需要将它从原来频数对应的双向链表中删除
deleteFromList(node);
node->freq++;
/*
下面这个操作是为了防止当前 node 对应的是最小频数双向链表里的唯一节点，具体情况可分两种讨论
情况 ① 如果当前 node 对应的是最小频数双向链表里的唯一节点，那么在进行对其的 get操作后，它的频数 freq++，
原双向链表节点数目变为 0，则最小频数 minFreq++，即执行这个 if 操作
情况 ② 如果当前 node 对应的不是最小频数双向链表里的唯一节点，那么无需更新 minFreq
*/
if(hashFreq[minFreq]->L->next==hashFreq[minFreq]->R) minFreq++;
append(node);//加入新的频数对应的双向链表
return node->value;//返回该 key 对应的 value 值
}
else return -1;//缓存中不存在该 key
}（6）再来实现一下更新缓存数据的 put 函数
//更新缓存数据
void put(int key, int value) {
if(n==0) return;//缓存空间为 0 ，不可以加入任何数据
if(get(key)!=-1)//缓存中已经存在该 key，复用一个 get 操作，就可以完成该节点对应双向链表的更新
hashNode[key]->value=value;//把该节点在节点哈希表 hashNode 中更新
else//缓存中不存在该 key，需要把新节点插入到缓存空间中
{
if(hashNode.size()==n)//缓存空间已满
{
Node *node=hashFreq[minFreq]->L->next;//找到最小频数 minFreq 对应的双向链表的最久未使用的节点
deleteFromList(node);//在双向链表中删除该节点
hashNode.erase(node->key);//在节点哈希表中删除该节点
}
//缓存空间未满 and 已满两种情况，均需要把新节点加入缓存（双向链表和节点哈希表均需插入）
Node *node=new Node(key,value,1);//构造新节点，它的节点频数为 1
hashNode[key]=node;//插入节点哈希表
minFreq=1;//新插入的节点频数为 1，故最小频数应当变为 1
append(node);//插入频数为 1 对应的双向链表中
}
}（7）get 和 put 函数涉及到两个新的函数 deleteFromList 和 append，分别用于移除和插入双向链表中的对应节点数据，下面实现一下这两个函数
void deleteFromList(Node *node)
{
Node *pre=node->pre;
Node *next=node->next;
pre->next=next;
next->pre=pre;
}
void append(Node *node)
{
int freq=node->freq;
if(hashFreq.find(freq)==hashFreq.end())
hashFreq[freq]=new FreqList(freq);
FreqList *curList=hashFreq[freq];
Node *pre=curList->R->pre;
Node *next=curList->R;
pre->next=node;
node->next=next;
next->pre=node;
node->pre=pre;
}（8）完整代码及注释如下，以供大家参考，完成上述内容学习，顺便大家还可以解决一下 LeetCode 460 题
class LFUCache {
private:
//双向链表节点
struct Node{
int key;
int value;
int freq;//为每个双向链表的节点增加 freq 值，用于记录其被访问频数
Node *pre,*next;
Node(int key,int value,int freq)
{
this->key=key;
this->value=value;
this->freq=freq;
pre=nullptr;
next=nullptr;
}
};
//双向链表
struct FreqList{
int freq;//标识双向链表中节点的共同访问频数
Node *L,*R;
FreqList(int freq)//双向链表构造函数
{
this->freq=freq;
L=new Node(-1,-1,1);
R=new Node(-1,-1,1);
L->next=R;
R->pre=L;
}
};
int n;//缓存空间大小
/*
整个缓存中的节点最小访问频数， LFU 中为每一个频数构造一个双向链表，
当缓存空间满了时，首先需要知道当前缓存中最小的频数是多少，再需要找到
该最小频数下最久未使用的数据淘汰。想要在 O(1) 时间复杂度下完成上述
操作，处理使用双向链表结构，还需要动态记录维护缓存空间中最小访问频数 minFreq
*/
int minFreq;
unordered_map hashNode;//节点哈希表，用于快速获取数据中 key 对应的节点信息
unordered_map hashFreq;//频数双向链表哈希表，为每个访问频数构造一个双向链表，并且用哈希表联系二者关系
void deleteFromList(Node *node)
{
Node *pre=node->pre;
Node *next=node->next;
pre->next=next;
next->pre=pre;
}
void append(Node *node)
{
int freq=node->freq;
if(hashFreq.find(freq)==hashFreq.end())
hashFreq[freq]=new FreqList(freq);
FreqList *curList=hashFreq[freq];
Node *pre=curList->R->pre;
Node *next=curList->R;
pre->next=node;
node->next=next;
next->pre=node;
node->pre=pre;
}
public:
// LFU 缓存构造函数
LFUCache(int capacity) {
n=capacity;//初始化缓存空间
minFreq=0;//初始化最小访问频数为 0
}
//访问缓存数据
int get(int key) {
if(hashNode.find(key)!=hashNode.end())//缓存中存在该 key
{
Node *node=hashNode[key];//利用节点哈希表，O(1) 时间复杂度下定位到该节点
//每次 get 操作会将该节点访问频数 +1，所以需要将它从原来频数对应的双向链表中删除
deleteFromList(node);
node->freq++;
/*
下面这个操作是为了防止当前 node 对应的是最小频数双向链表里的唯一节点，具体情况可分两种讨论
情况 ① 如果当前 node 对应的是最小频数双向链表里的唯一节点，那么在进行对其的 get操作后，它的频数 freq++，
原双向链表节点数目变为 0，则最小频数 minFreq++，即执行这个 if 操作
情况 ② 如果当前 node 对应的不是最小频数双向链表里的唯一节点，那么无需更新 minFreq
*/
if(hashFreq[minFreq]->L->next==hashFreq[minFreq]->R) minFreq++;
append(node);//加入新的频数对应的双向链表
return node->value;//返回该 key 对应的 value 值
}
else return -1;//缓存中不存在该 key
}
//更新缓存数据
void put(int key, int value) {
if(n==0) return;//缓存空间为 0 ，不可以加入任何数据
if(get(key)!=-1)//缓存中已经存在该 key，复用一个 get 操作，就可以完成该节点对应双向链表的更新
hashNode[key]->value=value;//把该节点在节点哈希表 hashNode 中更新
else//缓存中不存在该 key，需要把新节点插入到缓存空间中
{
if(hashNode.size()==n)//缓存空间已满
{
Node *node=hashFreq[minFreq]->L->next;//找到最小频数 minFreq 对应的双向链表的最久未使用的节点
deleteFromList(node);//在双向链表中删除该节点
hashNode.erase(node->key);//在节点哈希表中删除该节点
}
//缓存空间未满 and 已满两种情况，均需要把新节点加入缓存（双向链表和节点哈希表均需插入）
Node *node=new Node(key,value,1);//构造新节点，它的节点频数为 1
hashNode[key]=node;//插入节点哈希表
minFreq=1;//新插入的节点频数为 1，故最小频数应当变为 1
append(node);//插入频数为 1 对应的双向链表中
}
}
};