【机器学习】--神经网络(NN)
简单介绍:
神经网络主要是默认人类脑结构进行的一种代码程序结构的表现,同时是RNN,CNN,DNN的基础。结构上大体上分为三个部分(输入,含隐,输出),各层都有个的讲究,其中,输入层主要是特征处理后的入口,含隐层用来训练相应函数,节点越多,训练出的函数就越复杂,输出层输出相应的预测结果,比较常见的就是多分类了。
算法特点:
1、神经网络属于有监督学习的一种;
2、计算复杂度比较高,因为增加了相应的激活函数,所以等于复合函数嵌套复合函数;
3、含隐层的神经元越多,计算函数便越复杂,但带来的好处是,不用过度考虑特征方程,较其它机器学习入门算法而言,省却了特征适配;
4、BP后向传播其实就是误差函数反推参数求导过程,不知道为什么网络上的很多博客都没有人点出来,可能是使用BP后向传播算法,让别人听起来更厉害一些吧;
5、需要考虑过拟合问题;
6、数学不好别看了,看前五条就行了。
学习神经网络的基本流程:
1、了解基础知识(简单的神经网络构造,激活函数,误差函数);
2、推导
3、完成代码
4、画图看效果
基础知识:
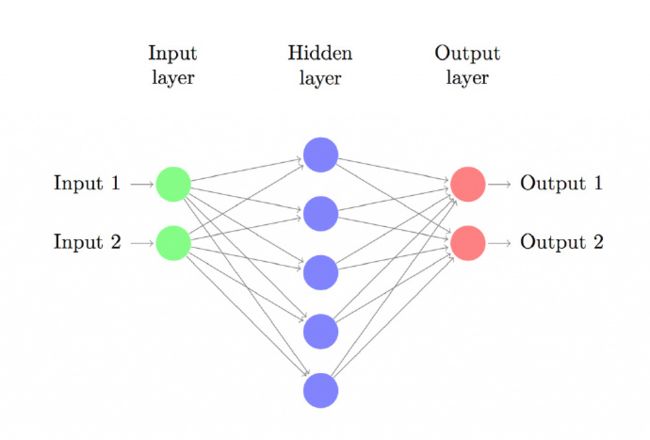
神经网络
上图建立具有一个输入层、一个隐藏层、一个输出层的三层神经网络。输入层的结点数由数据维度决定,这里是2维。类似地,输出层的结点数由类别数决定,也是2。(因为我们只有两类输出,实际中我们会避免只使用一个输出结点预测0和1,而是使用两个输出结点以使网络以后能很容易地扩展到更多类别)。每一个神经元都可以理解成一个函数,这个函数,也可以叫做激活函数,例如,输入神经元理解为Fin(x),含隐神经元理解为Fhn(x),输出神经元理解为Fou(x),每一层之间都是具有一个权重参数w(或者叫θ),每一层的输出乘上权重参数,都是下一层的输入,例如,Fin( input1 ) * w1 就是含隐层的输入,Fhn( Fin( input1 ) * w1 ) *w2 就是输出层的输入,Fou( Fhn( Fin(input1 ) * w1 ) * w2 )计算出最后的输出值。
常见的激活函数:
1、Sigmoid函数(也叫logistics函数)
2、Tanh函数(双曲函数)
3、sgn函数(阶跃函数)
4、ReLU函数
5、softmax函数
6、Linear函数
误差函数:
参考我写的机器学习--逻辑回归这篇文章吧,里面有提到,这里我们使用的是对数似然损失。这里特别说明一下,需要注意,交叉熵和对数似然很像,需要注意区别。
本次神经网络的三层形式:
输入层:特征,用x表示
输入层和含隐层之间的权重:使用w1表示
含隐层:tanh()
含隐层和输出层之间的权重:使用w2表示
输出层:softmax()
输出结果:Y表示(带上角标的那个我打不出来。。。)
softmax的函数如下:

其中,Yi表示第i类的输出,xi表示第i类的输入,底部的是所有输入的求和。
softmax的求导:
需要先行注意的是,底部xk的累加和是包含n个未知参数的,但在求导过程中,除了对其求到的那个未知参数外,其它参数,都视为常数项;
f(xi)对xi求导:

f(xi)对xa求导:
推导:
正向传播(也就是预测过程,即开始输入到最后输出的过程,求y):
y = softmax ( tanh ( x * w1 ) * w2 )
后向传播(求w2,w1):
后向传播就是倒着推,先推输出层到含隐层之间的权重w2,那么假设我们的真实值用大Y表示,我们的预测值用小y表示,那么他们之间的误差是Loss = ( Y - y) ,但由于我们softmax函数是指数形式,且本身是概率性问题,我们使用最大似然损失函数(也叫对数似然损失函数),Loss = -ln ( y ) ,(注,在书上见到的log其实就是ln,表示以e为底,表示的含义是,y是当前样本下预测模型得到的概率)
那么损失函数Loss =- ln ( y ) ,也就是说,要在损失最小的情况下求参数w2, 求参数求参数还要损失最小,梯度下降就可以了,已知梯度下降公式: w = w - α( ∂Loss / ∂w);
那么令 结果 a = tanh(x*w1)* w2
求取过程如下:
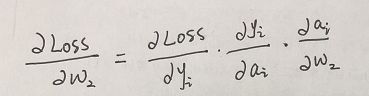
各项如下:
同理,进行对误差函数中的w1求导:
这样,后向传播也推导完了。
开始部署程序,程序分为以下几步:
1、获取数据进行处理
2、softmax公式构建
2.5、参数初始化(主要是权重)
3、前向传播(就是预测函数)构建
4、后向传播构建
5、误差函数构建
5.5、组合函数进行训练
6、训练结果评估
7、画图
本程序使用以下库,并使用以下全局变量:
import numpy as np
from sklearn.datasets import make_moons
import matplotlib.pyplot as plt
#学习速率
learning_rate = 0.01
#正则化参数
reg_lambda = 0.01
#特征数据
data_x = []
#data_y对应结果,mat_data_y结果的表示矩阵形式
data_y = []
mat_data_y = []
#权重参数
weights1 = []
weights2 = []
b1 = []
b2 = []
#误差
loss = []
第一步,数据获取:
def get_data():
global data_x,data_y
np.random.seed(0)
data_x, data_y = make_moons(200, noise=0.20)
max_y = max(data_y)
m = len(data_x)
#定义softmax函数
def softmax(x):
return np.exp(x)/(np.sum( np.exp(x) ,axis=1,keepdims=True))
第二点五步,参数初始化(主要是权重):
#input_layout_num是输入层层数,hide_layout_num是含隐层层数,output_layout_num是输出层层数
def set_params(hide_layout_num = 3 ):
global weights1, weights2 ,b1 ,b2
input_layout_num = len(data_x[0])
output_layout_num = len(mat_data_y[0])
# weights1 = np.ones((input_layout_num, hide_layout_num))
# weights2 = np.ones((hide_layout_num, output_layout_num))
weights1 = np.random.randn(input_layout_num, hide_layout_num)/ np.sqrt(input_layout_num)
weights2 = np.random.randn(hide_layout_num, output_layout_num)/np.sqrt(hide_layout_num)
# print(weights1)
# weights1 = np.ones((input_layout_num, hide_layout_num))
b1 = np.zeros((1,hide_layout_num))
b2 = np.zeros((1,output_layout_num))
第三步,前向传播(就是预测函数)构建:
#前向传播计算
def forward_propagation():
input_hide_calc_pe = np.dot(data_x ,weights1) + b1 #input_hide_calc_pe为输入层和含隐层之间的参数方程计算值
hide_activation_val = np.tanh(input_hide_calc_pe)#hide_activation_val是含隐层激活函数值
hide_output_calc_pe = np.dot(hide_activation_val, weights2) + b2#hide_output_calc_pe是含隐层和输出层之间的参数方程计算值
output_proba = softmax(hide_output_calc_pe)#out_proba是最后选择softmax函数计算出的概率,也就是预测值
return hide_activation_val,output_proba
#预测函数
def predict(x):
input_hide_calc_pe = np.dot(x ,weights1) + b1 #input_hide_calc_pe为输入层和含隐层之间的参数方程计算值
hide_activation_val = np.tanh(input_hide_calc_pe)#hide_activation_val是含隐层激活函数值
hide_output_calc_pe = np.dot(hide_activation_val, weights2) + b2#hide_output_calc_pe是含隐层和输出层之间的参数方程计算值
output_proba = softmax(hide_output_calc_pe)#out_proba是最后选择softmax函数计算出的概率,也就是预测值
result = np.max(output_proba,axis=1)
kind = np.argmax(output_proba,axis=1)
print(output_proba)
print("预测结果为第:" + str( kind) + "类\n"
+"预测系数为:" + str(result) )
return kind#返回每一组中最大数值对应位置的索引
第四步,后向传播构建:
#后向传播计算,output_proba输出层计算出的概率
def back_propagation( hide_activation_val, output_proba):
global weights2,weights1,b1,b2
feature_x_len,feature_x0_len = np.shape(data_x)
delta_w2_1 = output_proba
#(yi - 1 )
for i in range(feature_x_len):
delta_w2_1[i][data_y[i]] = delta_w2_1[i][data_y[i]] - 1
# (yi - 1 ) * tanh(w1 * xi)
delta_w2 = np.dot(hide_activation_val.T, delta_w2_1)
#b2 = yi - 1
delta_b2 = np.sum(delta_w2_1,axis=0,keepdims=True)
#[ ( yi - 1 ) * [ 1 - (tanh( w1 * xi ))^2 ] * w2 * xi ]
#1 - (tanh( w1 * xi ))^2
delta_w1_2 = (1 - hide_activation_val**2)
delta_w1_1 = np.dot(delta_w2_1 ,weights2.T)
delta_w1_3 = delta_w1_1 * delta_w1_2
delta_w1 = np.dot(data_x.T,delta_w1_3)
delta_b1 = np.sum(delta_w1_3,axis=0,keepdims=True)
delta_w2 = delta_w2 + reg_lambda * weights2
delta_w1 = delta_w1 + reg_lambda * weights1
weights1 = weights1 - learning_rate * delta_w1
b1 = b1 - learning_rate * delta_b1
weights2 = weights2 - learning_rate * delta_w2
b2 = b2 - learning_rate * delta_b2
第五步,误差函数构建:
#误差函数
def loss_func():
global loss
#Loss = - ln p(y|x) = - ln yi
loss_sum = 0.0
hide_activation_val, output_proba = forward_propagation()
for i in range(len(data_x)):
loss_sum = loss_sum + -1 * np.log( output_proba[i][data_y[i]] )
loss.append(1/len(data_x) * loss_sum)
第五点五步,训练:
def train(iter_num = 1,hide_layout_num = 3):
set_params(hide_layout_num)
for i in range(iter_num):
hide_activation_val,output_proba = forward_propagation()
back_propagation(hide_activation_val,output_proba)
loss_func()
第六步,训练结果评估:
#评估训练结果
def train_result_evaluate():
hide_activation_val, output_proba = forward_propagation()
output_result = np.argmax(output_proba,axis=1) #返回每一组中最大数值对应位置的索引
x_num = len(output_result)
real_num = 0.0
for i in range(x_num):
if output_result[i] == data_y[i]:
real_num += 1.0
score = real_num / x_num
print("本次样本数共:" + str(x_num) + "个\n"
+"训练后预测正确数量:"+ str(real_num) + "个\n"
+"正确率为:" + str(score * 100 ) + r'%' )
#画决策边界
def show_decision_pic():
# Set min and max values and give it some padding
x_max = max(data_x[:,0]) + 0.5
x_min = min(data_x[:,0]) - 0.5
y_max = max(data_x[:,1]) + 0.5
y_min = min(data_x[:,1]) - 0.5
range_space = 0.01
# Generate a grid of points with distance h between them
feature_x1 = np.arange(x_min, x_max, range_space) #其横向特征最大最小生成的范围值
feature_x2 = np.arange(y_min, y_max, range_space) #其纵向特征最大最小生成的范围值
x1, x2 = np.meshgrid(feature_x1, feature_x2) #将特征变化成行列相等的矩阵
# Predict the function value for the whole gid
feature = np.c_[x1.ravel(), x2.ravel()] #拼接成二维矩阵
print(np.shape(feature))
Z = predict(feature)
print(Z)
Z = Z.reshape(x1.shape)
# Plot the contour and training examples
plt.contour(feature_x1, feature_x2, Z)
plt.scatter(data_x[:, 0], data_x[:, 1], c=data_y, cmap=plt.cm.Spectral)
plt.show()
def show_loss_pic():
plt.figure(2)
plt.plot(loss)
plt.show()
运行程序:
if __name__ == "__main__":
get_data()
train(iter_num=20000,hide_layout_num=3)
print("初始loss:" + str(loss[0]))
print("最终loss:" + str(loss[-1]))
train_result_evaluate()
show_decision_pic()
show_loss_pic()
#这里进行一个单点预测
predict(data_x[-5])
看一下结果:
决策边界如下:

误差损失逐渐收敛:
误差值:
最后的单点预测(因为两类分别是用0和1表示的,所以第一类是第[0]类,第二类是第[1]类):
关于关于程序中权重初始化的说明(对应在set_param函数):
关于程序中,权重为什么是这样设置,还不是像基础的机器学习方法,设置全0或全1矩阵,原因就是因为,如果设置相同矩阵,那么所有神经元计算出来的结果是一样的,反向传播时,计算的梯度就一样了,参数就会一样,具体说明,请参考引用【4】.
写在最后,可以看出来,神经网络的计算比之前基础机器学习稍稍复杂一些,但套路还是一样的,就是多了一点,但好处也可以从图中看出来,尤其是和之前的逻辑回归比较后更容易得出鲜明结论,神经网络省去了找寻复杂特征方程的选择,神经元的多少就会决定自己处理的特征的复杂度。
比如使用30层含隐层,迭代2w次,看下效果
但这样的情况,就过拟合了,并不平滑,这样做出来的权重和函数,就不是预测了,无法体现我们做出来的东西的是具有通用适配性的。
图文知识及引用参考:
【1】softmax的推导: http://blog.csdn.net/behamcheung/article/details/71911133
【2】看了这篇文章,开始尝试写神经网络: http://python.jobbole.com/82208/
【3】实际上,【2】是翻译的github上的一篇文章( 打开ipynb格式): https://github.com/dennybritz/nn-from-scratch
【4】权重初始化的选择原因: http://blog.csdn.net/bixiwen_liu/article/details/52956727
【5】python绘图的函数说明: https://www.cnblogs.com/shuhanrainbow/p/6282452.html
【6】如何画等高线: https://zhidao.baidu.com/question/922394146083399819.html