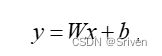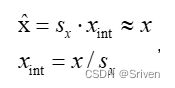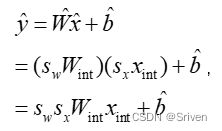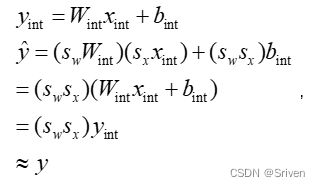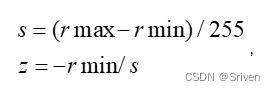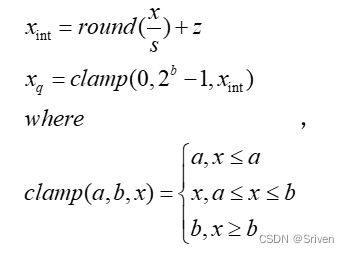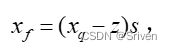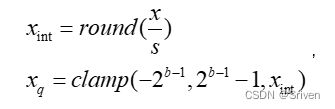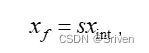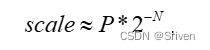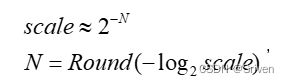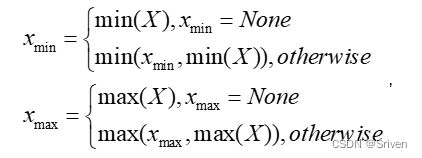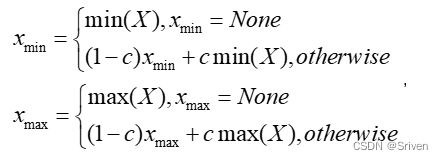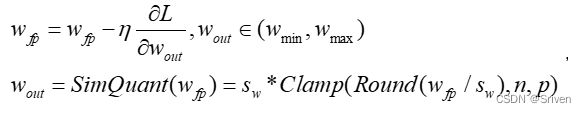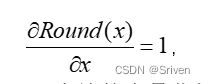深度学习量化总结(PTQ、QAT)
背景 目前神经网络在许多前沿领域的应用取得了较大进展,但经常会带来很高的计算成本,对内存带宽和算力要求高。另外降低神经网络的功率和时延在现代网络集成到边缘设备时也极其关键,在这些场景中模型推理具有严格的功率和计算要求。神经网络量化是解决上述问题有效方法之一,但是模型量化技术的应用会给模型带来额外噪音,从而导致精度下降,因此工程师对模型量化过程的理解有益于提高部署模型的精度。
目录
1. 量化基础知识
1.1 量化理论
1.2 Uniform Affine Quantizer(非对称量化)
1.3 Uniform symmetric quantizer(对称量化)
2. 比例因子如何求得
2.1 饱和量化与不饱和量化
2.2 量化策略
3. 量化的粒度
4. 量化方法
4.1 训练后量化PTQ
4.2 量化感知训练QAT
5. 量化总结
1. 量化基础知识
1.1 量化理论
量化实际上就是把高位宽表示的权值和激活值用更低位宽来表示。定点运算指令比浮点运算指令在单位时间内能处理更多数据,同时,量化后的模型可以减少存储空间。假设一次浮点运算为:
(1)
为了从浮点运算转移到高效的定点运算,我们需要一种将浮点向量转换为整数的方案。浮点向量x可以近似表示为标量乘以整数值向量:
(2)
其中,sx是浮点比例因子,xint是整数向量,例如INT8。我们将向量的量化版本表示为x'。通过量化权重和激活,我们可以写出公式(1)的量化版本:
(3)
请注意,对权重和激活分别使用单独的比例因子sx和sw。这提供了灵活性并减少了量化误差。由于每个比例因子应用于整个张量,因此该方案允许将比例因子从等式(3)中的累加中分离出来,并以定点格式执行MAC操作。现在有意忽略偏置量化,因为偏置通常存储在较高的比特宽度(32比特)中,其比例因子取决于权重和激活的比例因子。一般来说,偏置的比例因子为权重和激活的比例因子的乘积,这样做的好处是可以把sx和sw作为一个公因项提取出来,如下面的公式所示:
(4)
从以上的阐述不难看出,如何求比例因子是关键所在。
1.2 Uniform Affine Quantizer(非对称量化)
非对称量化由三个量化参数定义:比例因子s、零点z和比特宽度b。比例因子和零点用于将浮点值映射到整数网格,其size取决于比特宽度。比例因子通常表示为浮点数,并指定量化器的步长。零点是一个整数,确保实零(real zero)被量化而没有误差。这对于确保诸如零填充或ReLU之类的常见操作不会引起量化误差非常重要。
下图是一个uint8非对称量化的映射过程:
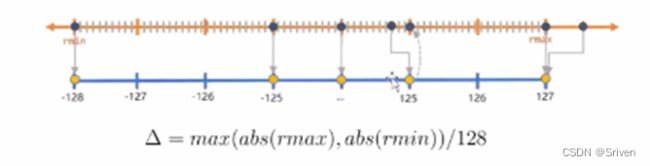
首先,量化前要计算比例因子,包括步长和零点两个量化参数。比例因子就是用来保证浮点区间内的变量都能无一缺漏的映射到要量化bit数的取值区间内。其中,步长和零点的计算公式如下:
(5)
这里要重点说下零点z,也叫做偏移,为何这里需要零点?实际上,浮点型的0会映射到零点,这个零点是一个整型数,用来确保0没有量化误差。具体就是,0有特殊意义,比如padding时,0值也是参与计算的,浮点型的0进行8bit量化后还是0就不对了,所以加上这个零点后,浮点型0就会被映射到0-255这个区间内的一个数,这样的量化就更精确。就相当于让映射后区间整体偏移,浮点最小值对应0。计算完量化因子,再从浮点区间任取一值的量化过程,
(6)
其中clamp用于将超出范围的值截断,因为xint有可能溢出。反量化时的公式为:
(7)
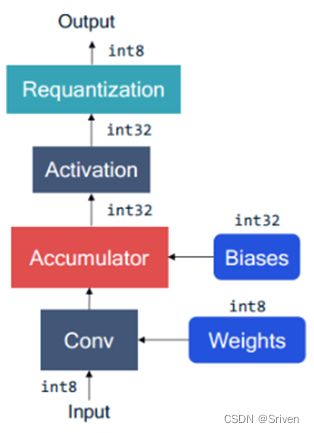
接下来我们模拟一层卷积定点运算过程,图1中表示了卷积层的定点量化计算过程。计算过程中 biases(b)、weight(w)、input(x) 和output(y) 全部为定点格式。计算公式如下:
y = Clamp(Round([(x-x_z)*s_x*(w-w_z)* s_w +(s_x*s_w)*(b-b_z)]/s_y))
红色部分是对输入进行反量化为浮点型,蓝色部分对权重进行反量化为浮点型,绿色部分对偏置反量化为浮点型,橙色部分对输出重量化为INT8类型,该式子还可以展开写出来,但是也可以看出来这一系列计算可能比浮点计算还要复杂。
图1 卷积层的定点量化计算过程
1.3 Uniform symmetric quantizer(对称量化)
对称量化是非对称量化的简化版本,即对称量化就是非对称量化中z=0的情况,下图是一个INT8对称量化的映射过程:
因此对称量化的公式为:
(8)
对称量化的反量化为:
(9)
如图1中使用对称量化的公式为:
y = Clamp(Round([(scale_x*x)*(scale_weight*w)+(scale_x*scale_w)*b]/scale_y))
= Clamp(Round( (x*w+b)*(scale_x*scale_w)/scale_y))
= Clamp(Round( (x*w+b)*scale))
红色部分是对输入进行反量化为浮点型,蓝色部分对权重进行反量化为浮点型,绿色部分对偏置反量化为浮点型,橙色部分对输出重量化为INT8类型,紫色部分可以提前计算好。然而scale还是一个浮点值,对于一些不支持浮点计算的硬件平台来说,可以将scale转成定点:
(10)
其中N和P都是整数,可以通过统计得出误差最小的N和P,这样上面的式子就可以表示为:
y= Clamp( Round( (x*w+b)*P>>N ) )
更进一步的,公式(10)可以修改为:
(11)
那么上面的式子就可以更加精简:
y= Clamp( Round( (x*w+b)>>N ) )
这种方式会带来更大的误差,这就需要后面提到的QAT来恢复精度。
2. 比例因子如何求得
比例因子可以利用一些标准来决定。前文中的量化参数是根据浮点值的最大最小值计算出,这种计算比例因子实际是有问题的,这种属于不饱和的线性量化,会导致精度损失较大。
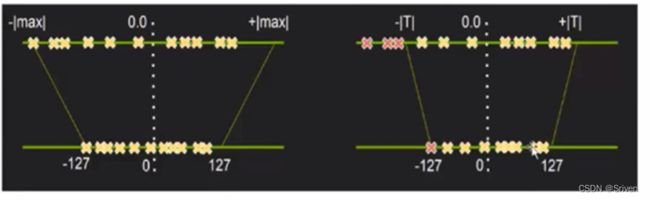
图2.左图不饱和量化,右图饱和量化
2.1 饱和量化与不饱和量化
首先左边的图(不饱和量化),上面是未量化的浮点区间,下面是要映射的int8区间。可以看到负值取值更大一点,就假设取这个值作为阈值,而正数最大值这边可能只有负值这边大小的一半,所以这个点量化后可能只映射到0-127的一半处,假设是64,所以量化后64-127这个区间显然就被浪费了;再假如负数最大值处是一个噪声点,只占激活值的一小部分甚至一个,而正值这边的值占比大的话,那么量化之后这些有效值就会压缩到一个很小的区间,然后精度损失就会比较大。
饱和量化算法是找到一个合适的阈值,如右图,把超出范围的噪声点的值都设为[T],然后量化之后,值会非常均匀的分布在(-127-127)这个区间。
2.2 量化策略
从第一节的介绍中我们不难发现,为了计算scale和zero_point我们需要知道 FP32 weight/activiation的实际动态范围。对于推理过程来说,weights是一个常量张量,不需要额外数据集进行采样即可确定实际的动态范围。但是activation的实际动态范围则必须经过采样获取(一般把这个过程称为数据校准(calibration))。目前各个深度学习框架中,使用最多的有最大最小值(MinMax),滑动平均最大最小值(MovingAverageMinMax)和KL距离(Kullback–Leibler divergence)三种。
2.2.1 最大最小值(MinMax)
这是最简单也是使用比较多的一种采样方法。它的基本思想是直接从FP32张量中选取最大值和最小值来确定实际的动态范围,如下公式所示:
(12)
对weights而言,这种采样方法是不饱和的。这种算法的优点是简单直接,但是对于activation而言,如果采样数据中出现离群点,则可能明显扩大实际的动态范围,比如实际计算时99%的数据都均匀分布在[-100, 100]之间,但是在采样时有一个离群点的数值为10000,这时候采样获得的动态范围就变成[-100, 10000]。
2.2.2 滑动平均最大最小值(MovingAverageMinMax)
与MinMax算法直接替换不同,MovingAverageMinMax会采用一个超参数c (Pytorch 默认值为0.01)逐步更新动态范围。公式如下:
(13)
这种方法获得的动态范围一般要小于实际的动态范围。对于weights而言,由于不存在采样的迭代,因此MovingAverageMinMax与MinMax的效果是一样的。MovingAverageMinMax常用在计算activation的比例因子。
2.2.3 KL距离(Kullback–Leibler divergence)
量化是对原始FP32数据的一种重新编码。一般认为量化之后的数据分布与原始分布越相似,量化对原始数据信息的损失也就越小。KL距离一般被用来度量两个分布之间的相似性,是一种量化两种概率分布P和Q之间差异的方式,又叫相对熵。KL散度能帮助我们度量使用一个分布来近似另一个分布时所损失的信息量。其基本公式如下:
(14)
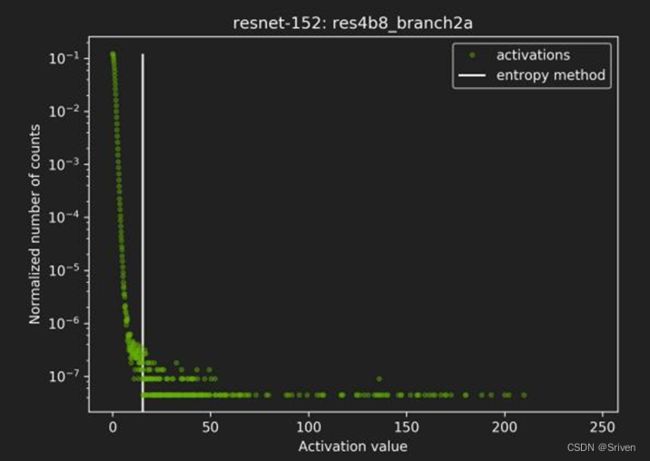
其中P,Q表示两个不同的分布。动态范围的选取直接决定了量化数据的分布情况,处于动态范围之外的数据将被映射成量化数据的边界点。如图3所示,横坐标表示activation的取值,纵坐标表示每个取值的归一化统计个数。从图可以看出绝大部分数值都分布在白色直线的左端。通过KL距离采样方法就会将动态范围限制在白线左侧的部分,白线右边的值将都会被映射成量化数据的最大值。
图3 KL距离动态范围选取例子
KL 距离采样方法通过直方图来模拟两个分布。Nivdia提供的伪代码如下:
| 01 Input: FP32 histogram H with 2048 bins: bin[ 0 ], …, bin[ 2047 ] |
| 02 For i in range( 128 , 2048 ): |
| 03 reference_distribution_P = [ bin[ 0 ] , ..., bin[ i-1 ] ] // 获取第i个bin |
| 04 outliers_count = sum( bin[ i ] , bin[ i+1 ] , … , bin[ 2047 ] ) |
| 05 reference_distribution_P [ i-1 ] += outliers_count |
| 06 P /= sum(P) // 归一化P |
| 07 candidate_distribution_Q = quantize [ bin[ 0 ], …, bin[ i-1 ] ] into 128 levels |
| 08 expand candidate_distribution_Q to ‘ i ’ bins |
| 09 Q /= sum(Q) // 归一化Q |
| 10 divergence[i]=KL_divergence(reference_distribution_P candidate_distribution_Q) |
| 11 End For 12 Find index ‘m’ for which divergence[m] is minimal 13 threshold = (m * 0.5)*(width of a bin) |
第1行表示将所有的浮点数值放入2048个直方桶里,第3行表示通过桶的位置来确定数据的动态范围。假设我们选第i个bin对应的值作为动态范围的右端边界。动态范围右边的数据都被映射到量化边界点,因此动态范围右边的数据被统一放到了第i-1个桶里。 因为 KL 距离要求两个分布必须相同的元素个数,第 8 行对候选分布进行了扩充操作。下面用一个简单的例子我们看一下第 7 行的quantize操作以及第 8 行的expand操作。假设P有 8 个桶,quantize之后有两个桶。quantize 不是桶上面介绍的量化公式来计算的,而是通过合并操作来处理。因为 8/2=4,所以相邻的4个桶会合并成一个,即:
P = [ 1, 0, 2, 3, 5, 3, 1, 7] =>[1 + 0 + 2 + 3 , 5 + 3 + 1 + 7] = [6, 16]
所以candidate_distribution_Q=[6,16]。因为P有8个元素,我们必须将 candidate_distribution_Q也转换成8个元素才能计算KL距离。在转换的过程中,原始 P 中为0的位置仍将为0。然后统计每个部分的非零个数作为转换系数。因为P的前4个元素有3个非零值,后四个元素有4个非零值,所以:
Q = [ 6/3, 0, 6/3, 6/3, 16/4, 16/4, 16/4, 16/4] = [ 2, 0, 2, 2, 4, 4, 4, 4]
下面是网上的一张步骤图:
图4 KL量化步骤
下面是一些常见问题以及解答:
- 将所有的浮点数值放入2048个直方桶里是什么意思,为什么是2048?
答:将所有的浮点数值放入2048个直方桶里表示的是将所有的浮点数值等距离的划分为2048个区间,也就是2048个直方桶,每个直方桶的值就是在该区间的个数。至于为什么是2048,这是Nvidia官方给出的值,如果数据量很大的话,也可以使用4096,一般来说2048就已经够了。
2.第二行代码为什么从128开始?
答:这里考虑的是ReLU激活,激活值都是大于0的数,如果截断的长度为128的话,那么我们直接一一对应就好了,即一个桶对应一直值,例如在第5个桶里的浮点数值就可以直接量化为5,完全不用衰减因子。如果激活值的范围是正负都有,那就从255开始。
3.为什么截断区外的值加到截断样本P的最后一个值上?
答:我的理解是截断区之外的值都会量化到截断点处,例如大于127的值都截断为127,知乎上的一个网友的回答是:第一是求P的概率分布时,需要P的总值,第二是尽可能地将截断后的信息加进来。(有点道理,但是不多)
4.第 7 行的quantize操作以及第 8 行的expand操作是什么意思?
答:上面也解释过了,这里再具体说下。首先第7行的quantize指的是将原始浮点值的直方图分布量化到128个桶里面,也就是将浮点数值量化到0-127,只不过这里量化的是直方图分布,例如将[ 1, 0, 2, 3, 5, 3, 1, 7]这个分布量化成两个桶,[ 1, 0, 2, 3, 5, 3, 1, 7] =>[1 + 0 + 2 + 3 , 5 + 3 + 1 + 7] = [6, 16],也就是说将前面四个桶量化成了6,后面四个桶量化成了16,如果这里是二值化,那么就是将前面6个浮点数映射成0,后面16个浮点数映射成1。那么expand操作又是什么呢?其实expand操作就相当于反量化了,将[6,6,6,6,16,16,16,16]反量化为[ 6/3, 0, 6/3, 6/3, 16/4, 16/4, 16/4, 16/4] = [ 2, 0, 2, 2, 4, 4, 4, 4],为什么6/3,16/4,因为在量化[ 1, 0, 2, 3, 5, 3, 1, 7]的时候是用加和量化的,反量化就是除以该部分的非零元素个数了。然后再分别得到两个集合的概率分布,计算这两个集合的KL距离。
总结一下:一般来说,对activation推荐使用KL散度量化。从上面的复杂介绍中我们可以看出: KL距离采样方法从理论上似乎很合理,但是也有几个缺点:1)动态范围的选取相对耗时。2)上述算法只是假设左侧动态范围不变的情况下对右边的边界进行选取,对于 ReLU这种数据分布的情况可能很合理,但是如果对于右侧数据明显存在长尾分布的情况可能并不友好。除了具有像ReLU等这种具有明显数据分布特征的情况,其他情况我们并不清楚从左边还是从右边来确定动态范围的边界。3)quantize/expand 方法也只是一定程度上模拟了量化的过程。
3. 量化的粒度
逐层量化(per-tensor):指定一个量化器(由尺度s和零点z定义)对张量进行量化。如果想让精度进一步提升,可以采用对张量的每个卷积核都使用对应的量化器。
逐通道量化(per-channel):对每个卷积核有不同的量化器。
对于激活输出我们不考虑逐通道量化,因为这会使卷积操作和矩阵乘操作中的内积计算变得复杂。“逐层量化”和“逐通道量化”都支持高效的点乘操作和卷积实现,因为这两种量化方式中量化参数在每个卷积核中都是固定的常量。
4. 量化方法
这一部分介绍实际场景中常用的两个量化方法。
4.1 训练后量化PTQ
字面意思,整个模型(浮点型的)训练完成后再单独把权值和激活值拿出来量化。过程中无需对原始模型进行任何训练,只对几个超参数调整就可完成量化过程。
4.1.1 只对权重量化
只量化权重和偏置,权重和偏置的比例因子一致。如果只是想为了方便传输和存储而减小模型大小,而不考虑在预测时浮点型计算的性能开销的话,这个量化很有用。
4.1.2 量化权重和激活值
激活值不像权值那样有固定数量,所以这时就得需要标定数据了,即计算激活值的动态范围,求得比例因子,然后再量化。一般使用1024张图片数据就足够估算出激活值的动态范围了。一般来说在PTQ中,权重使用MinMax量化,激活值使用滑动平均最大最小值或KL散度量化,偏置的比例因子为权重和激活值的比例因子的乘积。
4.1.3 总结
总结一下PTQ的大致过程:
- 准备训练好的浮点模型;
- 将训练好的浮点模型中的BN折叠,这一步很重要;
- 准备校准数据集,1024张左右就够了;
- 将校准数据集喂到模型中,把每一层的权重值和激活值拿出来,激活值是动态的,因此要取平均激活值;
- 使用Min-Max量化权重,得到比例因子数组scale_w;
- 使用KL散度或滑动平均最大最小值量化激活值,得到比例因子数组scale_a;
- 偏置的比例因子为scale_w*scale_a,量化偏置;
4.2 量化感知训练QAT
训练时量化方法相比于训练后量化,能够得到更高的精度,即使是逐层量化甚至是4bit 量化也能取得很高的精度。因此量化过程也会相对复杂一点。训练时量化对于权重和激活输出采用模拟量化操作来衡量量化效果。对于反向传播,使用“直通估计器”去建模量化。注意,在前向和反向传播计算中,使用的都是模拟量化的权重和激活输出,也保留浮点型权重,并且在梯度更新的过程中更新它们。这样可以确保使用较小的梯度更新逐步更新权重,而不会造成梯度满溢。更新的权重被量化,然后用于后续的前向和反向传播计算。
模拟量化操作是在训练时就进行量化的,操作实际包括一个量化再紧跟一个逆量化。具体的,就是在前向传播的时候(forward)模拟了量化的这个过程,在forward时首先会把权值和激活值量化到8bit再反量化回有误差的32bit,整体训练还是浮点,反向传播(backward)的时候求得的梯度是模拟量化之后权值的梯度,用这个梯度去更新量化前的权值。这种做法将量化中的取整误差和截断误差带入到了总损失中,让模型在训练过程中去适应这种误差。对于SGD,更新方式如下:
(15)
由于模拟量化方程的导数几乎在各个位置均为0(连续的浮点数量化映射成了离散的点),故在反向传播求梯度时无法求得,解决这个问题的一种方法是使用直通估计器(straight-through estimator STE,Bengio et al. 2013)来近似梯度,它将舍入算子的梯度近似为 1。
(16)
利用这个近似值,可以从方程(15)中计算出量化操作的梯度。为了清楚起见,默认使用对称量化,即 z = 0,但同样的结果适用于非对称量化,因为零点是一个常数。我们使用 n 和 p 来定义整数量化范围,如 n = qmin/sw , p = qmax/sw。方程(15)的梯度与它的输入wfp被如下定义:
(17)
5. 量化总结
并不是所有的模型,都很适合量化。在实际的生产环境中,我们经常会遇到一些模型,量化之后精度不好,其根本原因是因为浮点阶段的模型并不适合量化。 这里说明一些常见的不适合量化的浮点情况。在实际执行的时候,可以通过 debug 工具去发现模型当中不适合量化的部分。受限于量化的方法和编译器的限制,目前量化的 op 实现,会有一些限制或者误差。这种算子的误差一般有两种体现,第一种是 QAT 的时候精度会有影响(情况很少),第二种是 QAT 转 Quantized 的时候精度会有影响。这里使用如下表格简单列出一些常见的情况。
| 代表OP |
不适合量化的原因 |
| 带有Cos,Exp,Pow,Sin,Sqrt,Sigmoid等数学计算的OP |
查表实现,误差较大 |
| 大尺寸的Conv,AvgPool等 |
大 kernel size 导致统计量不准确,建议使用常规 kernel,比如 2x2,3x3 |
| 操作范围较大的 Concat |
和大 kenerl size 的 conv 类似,统计量不准 |
这里需要说明的是,并不是用了这些 op,精度一定会有问题,还需要结合模型,具体的算法,使用的频率来看。如果大量使用,则需要考虑这些 op 对量化的影响。
QAT 训练还是会有一定的模型训练能力。因此不适合量化,并不代表不能量化。某些情况下,即使出现上面的不适合量化的现象,仍然可以量化的很好。 因此,搭建量化友好的浮点模型,是为了在量化精度出现明显问题的时候,辅助分析浮点模型存在的问题。
问题1:模型中间输出很大。
检查模型中间输出一般是对浮点模型的数据分布(min,max 等)进行分析,是否有比较明显的异常值(如数值很大,有几千几万)。这种情况,会导致量化完精度下降很多。一般来说建议对输入做关于0对称的归一化,如果某些层的输出很大,建议检查模型结构,在浮点训练阶段,数值较大的层后面加上BN、ReLU等normlization的操作,或者对模型中范围比较大的输出层使用int16量化。
问题2:模型权重范围很大。
对于模型中范围较大的weight使用int16量化,或者适当调整weight decay。此外建议对输入做关于0对称的归一化。
QAT经验总结
除下述表格中的超参之外,其它参数建议在 QAT 阶段和浮点阶段保持一致。
| 超参 |
推荐配置 |
高级配置(如果推荐配置无效请尝试) |
备注 |
| LR |
从 0.001 开始,搭配 StepLR 做 2 次 scale=0.1 的 lr decay |
1. 调整 lr 在 0.0001->0.001 之间,配合 1-2 的 lr decay; |
|
| Epoch |
浮点 epoch 的 10% |
根据 loss 和 metric 的收敛情况,考虑是否需要适当延长 epoch。 |
|
| Weight decay |
与浮点一致 |
建议在 4e-5 附近做适当调整。weight decay 过小导致 weight 方差过大,过大导致输出较大的任务输出层 weight 方差过大。 |
|
| optimizer |
与浮点一致 |
有问题时,推荐尝试 SGD |
|
| transforms(数据增强) |
与浮点一致 |
QAT 阶段可以适当减弱,比如分类的颜色转换可以去掉,RandomResizeCrop 的比例范围可以适当缩小 |
数据增强减弱对浮点模型可能也会有收益 |
参考:
https://arxiv.org/abs/2106.08295
Int8量化-介绍(一) - 知乎
部署加速模型Int8量化_英伟达int8量化_CVer儿的博客-CSDN博客
【量化】——采用KL散度计算阈值_kl阈值_农夫山泉2号的博客-CSDN博客
深度学习模型量化(低精度推理)大总结_深度学习量化_爱上一只柠檬的pig_head的博客-CSDN博客
神经网络量化白皮书 - 简书
量化理解(Google量化白皮书《Quantizing deep convolutional networks for efficient inference: A whitepaper》)-阿里云开发者社区
Pytorch实现卷积神经网络训练量化(QAT) - 知乎
再读《神经网络量化白皮书》- 0x04 训练时量化(QAT) - 知乎
https://developer.horizon.ai/api/v1/fileData/horizon_j5_open_explorer_v1_1_33_cn_doc/plugin/source/tutorials/qat_experience.html