数据结构 栈和队列

数据结构 栈和队列

1. 栈(Stack)

1.1 概念

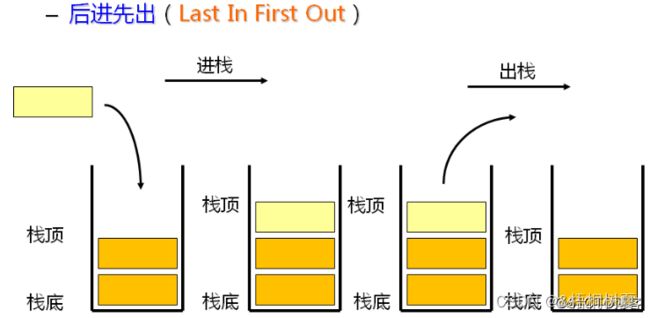
栈是一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作

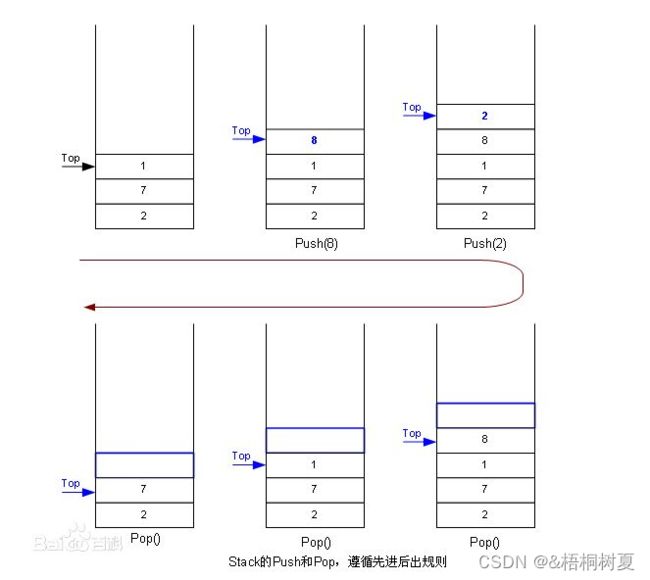
进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出的原则

压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶

出栈：栈的删除操作叫做出栈，出数据在栈顶

栈在现实生活中的例子：

1.2 栈的模拟实现

• MyStack构造

  package demo1;
  
  import java.util.Arrays;
  
  public class MyStack {
  
      int[] array;
      int size;
  
      public MyStack() {
          array = new int[3];
      }
  
      /*入栈方法*/
      public int push(int e) {
          ensureCapacity();
          array[size++] = e;
          return e;
  
      }
  
      /*出栈方法*/
      public int pop() {
          int e = peek();
          size--;
          return e;
      }
  
      /*获取栈顶元素*/
      public int peek() {
          if (empty()) {
              throw new RuntimeException("栈为空，无法获取栈顶元素");
          }
  
          return array[size - 1];
      }
  
      /*判断栈是否为空*/
      public boolean empty() {
          if (size == 0) {
              return true;
          }
          return false;
      }
  
      /*扩容*/
      public void ensureCapacity() {
          if (size == array.length) {
              array = Arrays.copyOf(array,size * 2);
          }
      }
  
      public void display() {
          for (int i = 0;i < this.size;i++) {
              System.out.print(this.array[i] + " ");
          }
      }
  }
  

• Main函数

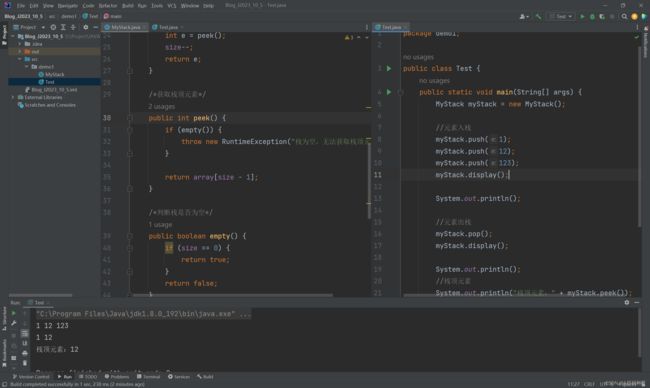
  package demo1;
  
  public class Test {
      public static void main(String[] args) {
          MyStack myStack = new MyStack();
  
          //元素入栈
          myStack.push(1);
          myStack.push(12);
          myStack.push(123);
          myStack.display();
  
          System.out.println();
  
          //元素出栈
          myStack.pop();
          myStack.display();
  
          System.out.println();
          //栈顶元素
          System.out.println("栈顶元素：" + myStack.peek());
      }
  }
  
  //执行结果
  1 12 123 
  1 12 
  栈顶元素：12
  

  

1.3 栈的使用

方法	功能
Stack()	构造一个空的栈
E push(E e)	将e入栈，并返回e
E pop()	将栈顶元素出栈并返回
E peek()	获取栈顶元素
int size()	获取栈中有效元素个数
boolean empty()	检测栈是否为空

package demo2;

import java.util.Stack;

public class Stack1 {
    public static void main(String[] args) {

        Stack<Integer> stack = new Stack<>();
        stack.push(1);
        stack.push(12);
        stack.push(123);
        stack.push(1234);
        stack.push(12345);

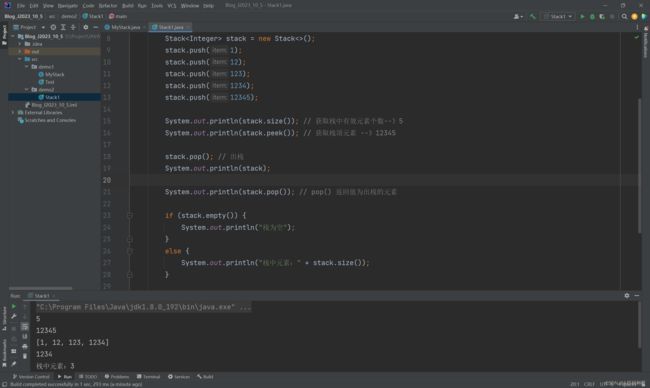
        System.out.println(stack.size()); // 获取栈中有效元素个数--》5
        System.out.println(stack.peek()); // 获取栈顶元素 --》12345

        stack.pop(); // 出栈
        System.out.println(stack);

        System.out.println(stack.pop()); // pop() 返回值为出栈的元素

        if (stack.empty()) {
            System.out.println("栈为空");
        }
        else {
            System.out.println("栈中元素：" + stack.size());
        }


    }
}

//执行结果
5
12345
[1, 12, 123, 1234]
1234
栈中元素：3

1.4 栈的应用场景

1. 改变元素的序列

   1. 若进栈序列为 1,2,3,4 ，进栈过程中可以出栈，则下列不可能的一个出栈序列是（）
   A: 1,4,3,2 B: 2,3,4,1 C: 3,1,4,2 D: 3,4,2,1
   
   2.一个栈的初始状态为空。现将元素1、2、3、4、5、A、B、C、D、E依次入栈，然后再依次出栈，则元素出栈的顺序是（ ）
   A: 12345ABCDE B: EDCBA54321 C: ABCDE12345 D: 54321EDCBA
   
   答案：C B
   

2. 将递归转化为循环

   比如：逆序打印链表

   void printList(Test2.ListNode head) {
           if (head == null) {
               return;
           }
   
           Stack<ListNode> stack = new Stack<>();
           ListNode cur = head;
           while(cur != null) {
               stack.push(cur);
               cur = cur.next;
           }
   
           while(!stack.empty()) {
               System.out.println(stack.pop().val + " ");
           }
       }
   

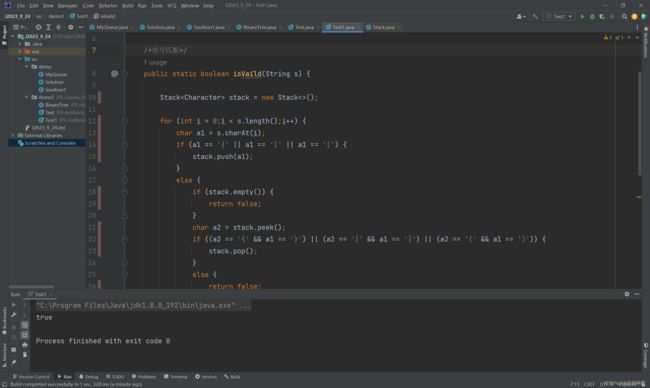
3. 括号匹配

   package demo1;
   
   import java.util.Stack;
   
   public class Test1 {
   
       public static boolean isVaild(String s) {
   
           Stack<Character> stack = new Stack<>();
   
           for (int i = 0;i < s.length();i++) {
               char a1 = s.charAt(i);
               if (a1 == '{' || a1 == '[' || a1 == '(') {
                   stack.push(a1);
               }
               else {
                   if (stack.empty()) {
                       return false;
                   }
                   char a2 = stack.peek();
                   if ((a2 == '{' && a1 == '}') || (a2 == '[' && a1 == ']') || (a2 == '(' && a1 == ')')) {
                       stack.pop();
                   }
                   else {
                       return false;
                   }
   
               }
           }
           if (!stack.empty()) {
               return false;
           }
           return true;
       }
   
   
   
   
   
       public static void main(String[] args) {
           String s = "(){}[]";
           System.out.println(isVaild(s));
   
       }
   }
   
   

   

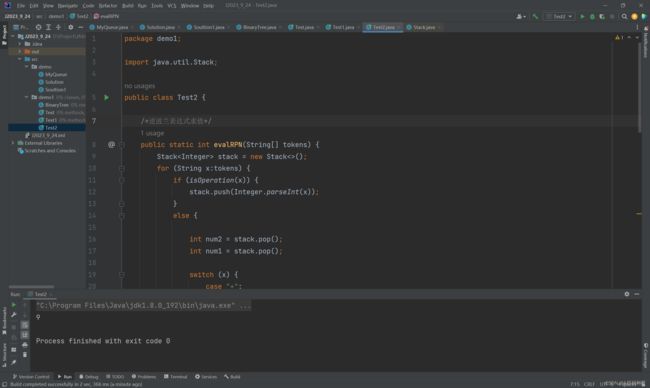
4. 逆波兰表达式求值

   package demo1;
   
   import java.util.Stack;
   
   public class Test2 {
   
       public static int evalRPN(String[] tokens) {
           Stack<Integer> stack = new Stack<>();
           for (String x:tokens) {
               if (isOperation(x)) {
                   stack.push(Integer.parseInt(x));
               }
               else {
   
                   int num2 = stack.pop();
                   int num1 = stack.pop();
   
                   switch (x) {
                       case "+":
                           stack.push(num1 + num2);
                           break;
                       case "-":
                           stack.push(num1 - num2);
                           break;
                       case "*":
                           stack.push(num1*num2);
                           break;
                       case "/":
                           stack.push(num1/num2);
                           break;
                   }
               }
           }
           return stack.peek();
       }
   
       public static boolean isOperation(String x) {
               if (x.equals("+") || x.equals("-") || x.equals("*") || x.equals("/")) {
                   return false;
               }
               return true;
           }
   
       public static void main(String[] args) {
           String[] s = {"2","1","+","3","*"};
           System.out.println(evalRPN(s));
       }
   }
   

   

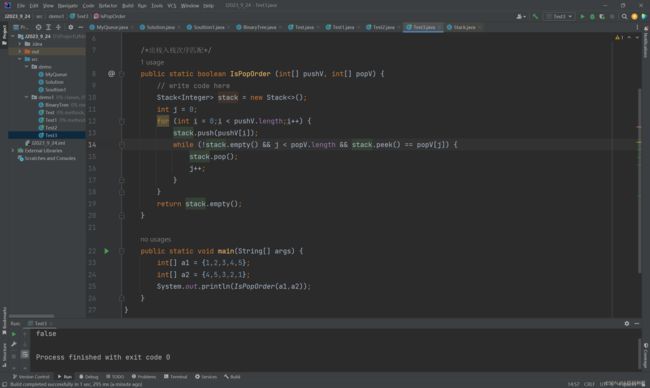
5. 出栈入栈次序匹配

   package demo1;
   
   import java.util.Stack;
   
   public class Test3 {
   
       /*出栈入栈次序匹配*/
       public static boolean IsPopOrder (int[] pushV, int[] popV) {
           // write code here
           Stack<Integer> stack = new Stack<>();
           int j = 0;
           for (int i = 0;i < pushV.length;i++) {
               stack.push(pushV[i]);
               while (!stack.empty() && j < popV.length && stack.peek() == popV[j]) {
                   stack.pop();
                   j++;
               }
           }
           return stack.empty();
       }
   
       public static void main(String[] args) {
           int[] a1 = {1,2,3,4,5};
           int[] a2 = {4,5,3,2,1};
           System.out.println(IsPopOrder(a1,a2));
       }
   }
   

   

6. 最小栈

   class MinStack {
   
       /*最小栈*/
       int[] array;
       int size;
   
       public MinStack() {
           array = new int[3];
       }
   
       public int push(int val) {
           ensureCapicity();
           array[size++] = val;
           return val;
       }
   
       public int pop() {
           if (empty()) {
               System.out.println("栈为空");
           }
           else {
               int e = top();
               size--;
               return e;
           }
           return 0;
       }
   
       public int top() {
           return array[size-1];
       }
   
       public int getMin() {
           int min = array[size-1];
           int x = size;
           while(x > 0) {
               if (array[x-1] < min) {
                   min = array[x-1];
               }
               x--;
           }
           return min;
       }
   
       public boolean empty() {
           return size == 0;
       }
   
       public void ensureCapicity() {
           if (size == array.length) {
               array = Arrays.copyOf(array,size * 2);
           }
       }
   }
   

2. 队列(Queue)

2.1 概念

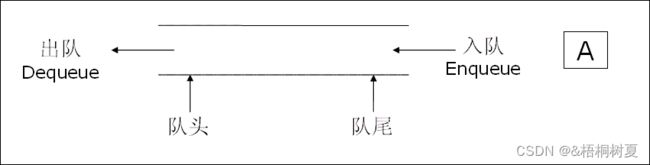
队列是一种只允许在一段进行插入数据操作，在另一端进行删除数据操作的特殊线性

队列遵循先进先出的原则，同时有以下两种操作：

入队列：进行插入操作，其一端称为队尾(Tail/Rear)

出队列：进行删除操作，其一端称为队头(Head/Front)

2.2 队列的模拟实现

在这里我们使用链式结构来实现队列

• MyQueue构造

  package demo3;
  
  public class MyQueue {
  
      public static class ListNode {
          ListNode next;
          ListNode prev;
          int val;
  
          public ListNode(int val) {
              this.val = val;
          }
      }
  
      ListNode first; // 队头
      ListNode last; // 队尾
      int size = 0;
  
      /*入队列--向双向链表位置插入新的节点*/
      public void offer(int e) {
          ListNode newNode = new ListNode(e);
          if (first == null) {
              first = newNode;
          }
          else {
              last.next = newNode;
              newNode.prev = last;
          }
          last = newNode;
          size++;
      }
  
      /*出队列--将双向链表的第一个节点删除*/
      public int poll() {
          int value = 0;
          if (first == null) { // 1.队列为空
              throw new RuntimeException("队列为空");
          }
          else if (first == last) { // 2.队列只有一个节点，直接删除
              first = null;
              last = null;
          }
          else { // 3.队列中有多个节点，将第一个节点删除
              value = first.val;
              first = first.next;
              first.prev.next = null;
              first.prev = null;
          }
          size--;
          return value;
      }
  
      /*获取队头元素--获取链表中第一个节点的值域*/
      public Object peek() {
          if (first == null) {
              return null;
          }
          return first.val;
      }
  
      public int size() {
          return size;
      }
  
      public boolean isEmpty() {
          return size == 0;
      }
  
      public void display() {
          ListNode cur = first;
          for (int i = 0;i < size;i++) {
              System.out.print(cur.val + " ");
              cur = cur.next;
          }
      }
  }
  

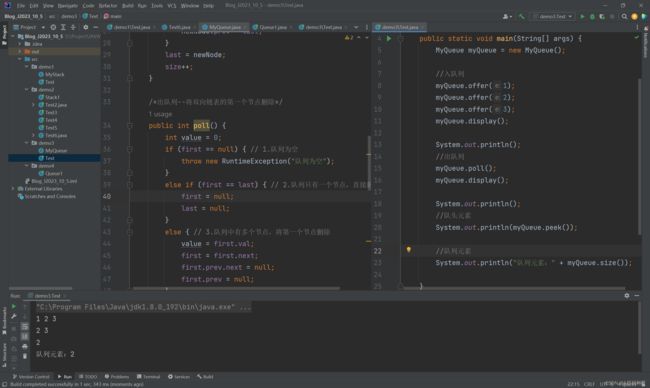
• Main函数

  package demo3;
  
  public class Test {
      public static void main(String[] args) {
          MyQueue myQueue = new MyQueue();
  
          //入队列
          myQueue.offer(1);
          myQueue.offer(2);
          myQueue.offer(3);
          myQueue.display();
  
          System.out.println();
          //出队列
          myQueue.poll();
          myQueue.display();
  
          System.out.println();
          //队头元素
          System.out.println(myQueue.peek());
  		
          //队列元素
          System.out.println("队列元素：" + myQueue.size());
      }
  }
  
  //执行结果
  1 2 3 
  2 3 
  2
  队列元素：2
  

  

2.3 队列的使用

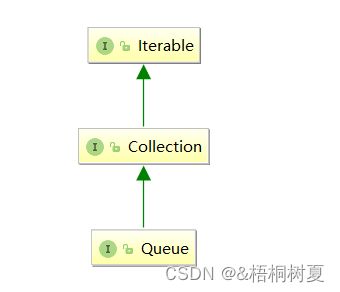
在Java中，Queue是个接口，底层是通过链表实现的：

方法	功能
boolean offer(E e)	入队列
E poll()	出队列
peek()	获取队头元素
int size()	获取队列中有效元素个数
boolean isEmpty()	检测队列是否为空

注：Queue是个接口，在实例化时必须实例化LinkListed的对象, 因为LinkedList实现了Queue接口

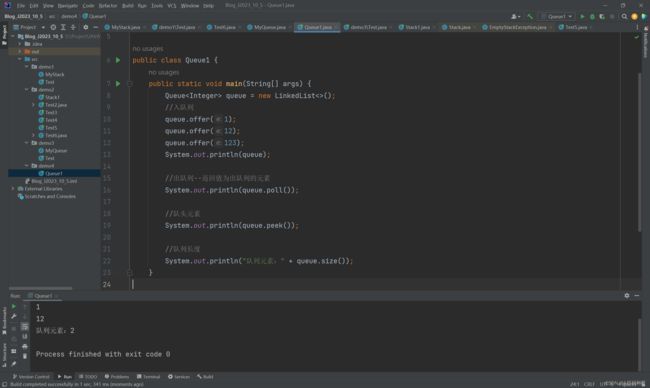
package demo4;

import java.util.LinkedList;
import java.util.Queue;

public class Queue1 {
    public static void main(String[] args) {
        Queue<Integer> queue = new LinkedList<>();
        //入队列
        queue.offer(1);
        queue.offer(12);
        queue.offer(123);
        System.out.println(queue);

        //出队列--返回值为出队列的元素
        System.out.println(queue.poll());

        //队头元素
        System.out.println(queue.peek());

        //队列长度
        System.out.println("队列元素：" + queue.size());
    }
}

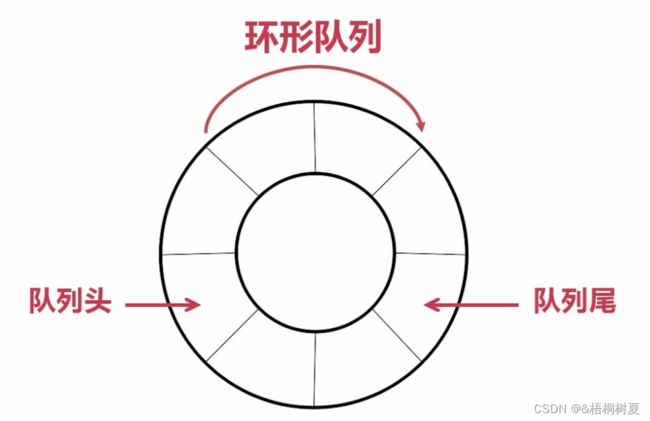
2.4 循环队列

实际上我们有时还会使用一种队列叫循环队列(环形队列),通常使用数组实现

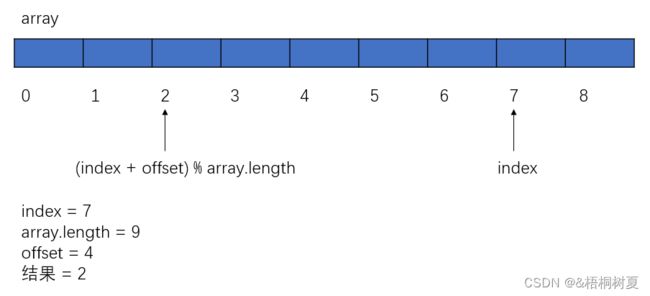
数组下标循环的小技巧

1. 下标最后再往后(offset小于array.length): index = (index+offset)%array.length

   

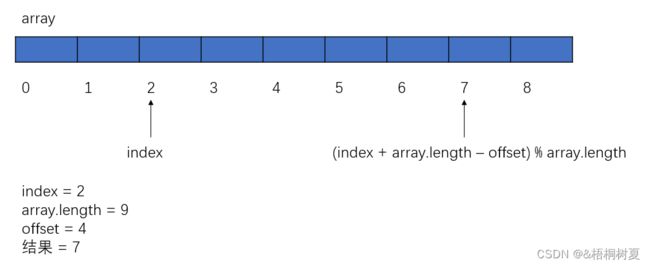
2. 下标最前再往前(offset小于array.length): index = (index + array.length - offset) % array.length

   

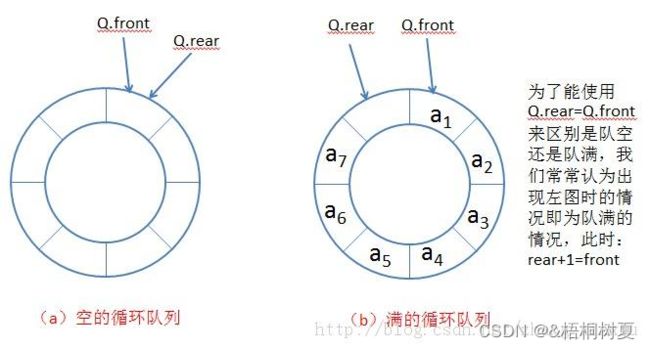
如何区分空与满

1. 通过添加size属性记录

2. 保留一个位置

3. 使用标记

   

在这里我们通过保留一个位置来进行代码实现：

package demo2;

class MyCircularQueue {

    public int[] elm;
    public int front; //队头
    public int rear; //队尾


    public MyCircularQueue(int k) {
        elm = new int[k+1];
    }

    /*入队*/
    public boolean enQueue(int value) {
        if (isFull()) {
            return false;
        }
        elm[rear] = value;
        rear = (rear+1)%elm.length;
        return true;
    }

    /*出队*/
    public boolean deQueue() {
        if (isEmpty()) {
            return false;
        }
        front = (front + 1)% elm.length;
        return true;
    }

    /*获得对头元素*/
    public int Front() {
        if (isEmpty()) {
            return -1;
        }
        return elm[front];
    }
    
    /*获取队尾元素*/
    public int Rear() {
        if(isEmpty()) {
            return -1;
        }
        int index = rear == 0 ? elm.length -1 : rear - 1;
        return elm[index];
    }
    
    public boolean isEmpty() {
        return front == rear;
    }
    
    public boolean isFull() {
        return (rear+1)% elm.length == front;
    }
}

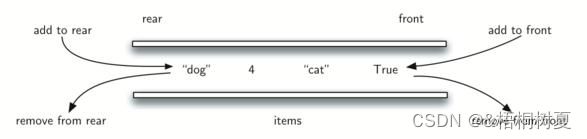
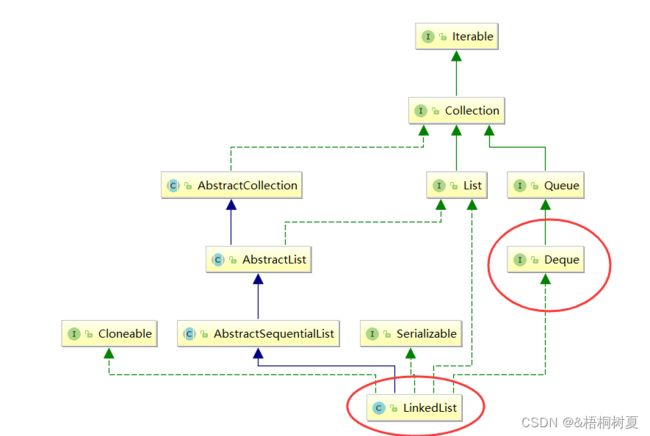
2.5 双端队列(Deque)

双端队列是指允许两端都可以进行入队和出队操作的队列，deque是"double ended queue" 的简称。那就说明元素可以从队头出队和入队，也可以coon队尾出队和入队

Deque是一个接口，使用时必须创建LinkedList的对象

栈和队列均可以使用Deque接口(本文仅做简单介绍)

Deque<Integer> stack = new ArrayDeeque<>(); //双端队列的线性实现
Deque<Integer> queue = new LinkedList<>(); //双端队列的链式实现

3. 双向操作

我们可以利用栈来实现队列，也可以利用队列来实现栈

3.1 用队列实现栈

package demo5;

import java.util.LinkedList;
import java.util.Queue;

public class MyStack {

    Queue<Integer> q1;
    Queue<Integer> q2;


    public MyStack() {
        q1 = new LinkedList<>();
        q2 = new LinkedList<>();
    }

    /*入栈*/
    public void push(int x) {
        if(!q1.isEmpty()) {
            q1.offer(x);
        }
        else if(!q2.isEmpty()) {
            q2.offer(x);
        }
        else {
            q1.offer(x);
        }
    }

    /*出栈*/
    public int pop() {

        if (empty()) {
            return -1;
        }

        if (!q1.isEmpty()) {
            int size = q1.size();
            for (int i = 0;i < size - 1;i++) {
                q2.offer(q1.poll());
            }
            return q1.poll();
        }
        else {
            int size = q2.size();
            for (int i = 0;i < size -1;i++) {
                q1.offer(q2.poll());
            }
            return q2.poll();
        }
    }

    /*获取栈顶元素*/
    public int top() {
        if (empty()) {
            return -1;
        }

        if (!q1.isEmpty()) {
            int size = q1.size();
            int x = -1;
            for (int i = 0;i < size;i++) {
                x = q1.poll();
                q2.offer(x);
            }
            return x;
        }
        else {
            int size = q2.size();
            int  x = -1;
            for (int i = 0;i < size;i++) {
                x = q2.poll();
                q1.offer(x);
            }
            return x;
        }
    }

    public boolean empty() {
        return q1.isEmpty() && q2.isEmpty();
    }
}

3.2 用栈实现队列

package demo5;

import java.util.Stack;

public class MyQueue {

    Stack<Integer> s1;
    Stack<Integer> s2;


    public MyQueue() {
        s1 = new Stack<>();
        s2 = new Stack<>();
    }

    /*入队列*/
    public void push(int x) {
        s1.push(x);
    }

    /*出队列*/
    public int pop() {
        if(empty()) {
            return -1;
        }
        if (s2.isEmpty()) {
            while(!s1.isEmpty()) {
                s2.push(s1.pop());
            }
        }
        return s2.pop();
    }

    /*获取队头元素*/
    public int peek() {
        if (empty()) {
            return -1;
        }
        if (s2.isEmpty()) {
            while(!s1.isEmpty()) {
                s2.push(s1.pop());
            }
        }
        return s2.peek();
    }

    public boolean empty() {
        return s1.empty() && s2.empty();
    }
}