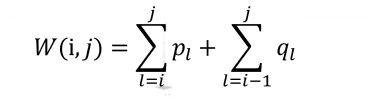算法学习-动态规划

动态规划

本博客结合了acwing算法基础课

为什么要使用DP

用分治法解决的问题中存在重叠子问题，分治方法将重复计算公共子问题，造成许多不必要的计算

使用DP的条件

1. 具有优化子结构
   原问题的优化解包含了子问题的优化解
2. 具有重叠子问题
   问题求解过程中很多子问题的解被重复利用

DP的理解方式

1. 状态表示：
   集合：所有选法的集合
   属性：状态集合里的最大值，最小值，数量
2. 状态计算：
   集合的划分
   划分原则：不漏

DP的时间复杂度分析

状态数量*计算每一个状态所需的时间复杂度

几种经典的DP问题

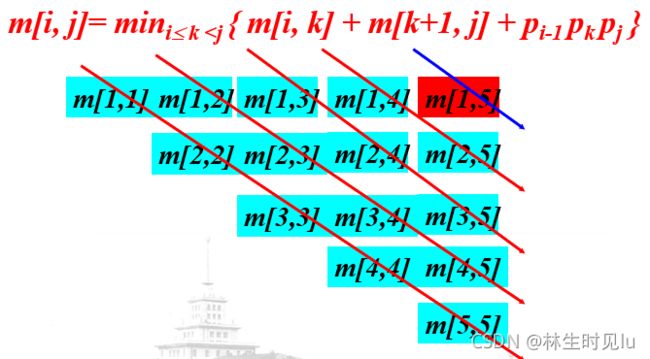
矩阵链乘法问题及其变式

1. 问题的定义
   
2. 问题的求解

• 一些记号：
  

• 证明优化子结构（反证）
  

• 证明重叠子问题
  

• 递归方程
  
  -== 算法伪代码，输出优化解==

注：计算顺序其实就对应了这张图

• 算法的时间复杂度和空间复杂度
  

最长公共子序列问题及其变式

1. 问题的定义
   
2. 问题的求解

• 一些记号
  
• 证明优化子结构
  
• 证明重叠子问题
  
• 递归方程
  
• 算法伪代码，输出优化解
  
  
  
• 算法的c++代码
  $f[i][j]$分成了

1. a[i],b[j]都不选:f[i-1][j-1];
2. a[i]没有在最后的公共子序列中:f[i-1][j]
3. b[j]没有在最后的公共子序列中:f[i][j-1];
4. a[i]=b[j],即ai在最后的公共子序列中：f[i-1][j-1]+1
   其中1包含于2,3两种情况中，所以1不用单独列出来

#include 
using namespace std;
const int N=1010;
int f[N][N];
char A[N],B[N];
int main()
{
    int n,m;
    int maxitem=0;
    cin>>n>>m;
    for (int i=1;i<=n;i++)
    cin>>A[i];
    for (int i=1;i<=m;i++)
    cin>>B[i];
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            {
                maxitem=max(f[i-1][j],f[i][j-1]);
                if(A[i]==B[j])
                maxitem=max(f[i-1][j-1]+1,maxitem);
            f[i][j]=maxitem;
            }
            
    cout<<f[n][m];

• 算法的时间复杂度
  

动态时间规整算法

1. 问题的定义
   
2. 问题的解决
   类似于最长公共子序列

背包模型

01背包

1. 问题的定义
   
2. 问题的求解

• 一些定义
  

• 递归方程
  

• 算法伪代码
  
  

• 算法c++代码

二维数组朴素写法

# include 
using namespace std;
const int N=1001;
int f[N][N];
int v[N];
int w[N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
    for(int i=1;i<=n;i++)
        for(int j=0;j<=m;j++)
        {
            f[i][j]=f[i-1][j];
            if(j>=v[i])
            f[i][j]=max(f[i-1][j],f[i-1][j-v[i]]+w[i]);
        }
    cout<<f[n][m];
}

一维数组优化写法

将二维数组优化为一维数组的思路：

1. 不需要保存任意前i种物品背包容量为j时的最大价值，只需要考虑最后一轮循环即前N种物品背包容量为j时的最大价值
2. 由于正序循环背包容量时$f[j]，即f[i][j]$状态的更新靠的是当前第i轮也就是$f[i][j-v[i]]$的已决策量来更新的，与应该靠上一轮$f[i-1][j-v[i]]$来更新不相符,故应该逆序循环背包容量k
3. 可以优化背包容量循环的结束条件为$j\ge v[i]$,因为若$j\le v[i]$表示第i个物品放不进背包，可直接结束循环

第i轮循环时，$f(j)$表示对i种物品背包容量为j时最大价值

# include 
using namespace std;
const int N=1001;
int f[N];
int v[N];
int w[N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
    for(int i=1;i<=n;i++)
        for(int j=m;j>=v[i];j--)
        {
            f[j]=max(f[j],f[j-v[i]]+w[i]);
        }
    cout<<f[m];
}

完全背包

第i个物品可以选无限个，直到装满

两维的朴素写法

原理$f(i,j)=max(f(i-1,j),f(i-1,j-v)+w,f(i-1,j-2v)+2w....)=max(f(i-1,j),max(f(i-1,j-v)+w,f(i-1,j-2v)+2w...)=max(f(i-1,j),f(i,j-v)+w)$

#include
using namespace std;
const int N=1001;
int f[N][N];
int v[N],w[N];
int main()
{
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	cin>>v[i]>>w[i];
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			{
			f[i][j]=f[i-1][j];
			if(j>=v[i])
			f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
			}
	cout<<f[n][m]<<endl;
	return 0;
}

优化为一维的写法

优化为一维的两种理解方式

• 直观理解：$f[j]$可以理解为当背包容量为j时所有可行的背包装填方法中总价值最大的那一个价值，我们可以把求解$f[j]$的问题划分为i类，每类代表最后一个装入背包的物品是第i个物品，而$f[j]$就是这i类中使得背包总价值最大的那一个，故$f[j]=max(f[j],f[j-v[i]]+w[i])$
• 通过代码的等价变形理解
  观察代码段

for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			{
			f[i][j]=f[i-1][j];
			if(j>=v[i])
			f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
			}

由于最后求解的问题只需要求$f[n][m]$没必要把每个状态的最优解都保存下来，所以i重循环做的过程中可以动态地更新一维数组，最后数组中保存下来的就是前n个物品中背包容量为j（j=0,1,2…m）时最大价值

f[0]=0;//初始状态，因为f已经设为全局变量所以这步可忽略
for (int i=1;i<=n;i++)//枚举物品
	for(int j=v[i];j<=m;j++)//枚举背包容量,循环开始条件是v[i]是因为j
		f[j]=max(f[j],f[j-v[i]]+w[i]);
cout<<f[m]<<endl;

线性DP

数字三角形

从起点走到$f(i,j)$所有路线的最大值等于从左上方和从正上方走，即$max(f(i-1,j-1),f(i-1,j))$

#include 
using namespace std;
const int N=510,inf=1e9;
int a[N][N],f[N][N];
int main()
{
    int n,maxnum=-inf;
    cin>>n;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=i;j++)
            cin>>a[i][j];
       
    for(int i=1;i<=n;i++)
        for(int j=0;j<=i+1;j++)
            f[i][j]=-inf;
    f[1][1]=a[1][1];
    for(int i=1;i<=n;i++)
        for(int j=1;j<=i;j++)
            f[i][j]=max(f[i-1][j-1]+a[i][j],f[i-1][j]+a[i][j]);
    for(int i=1;i<=n;i++)
        if(f[n][i]>=maxnum)maxnum=f[n][i];
    cout<<maxnum;
}

最长上升子序列

思路：状态表示$f[i]$存的是以第i个元素结尾的最长上升子序列的长度的最大值

# include 
using namespace std;
const int N=1010;
int f[N],a[N];
int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        f[i]=1;//作为计算f[i]分类时最长上升子序列长度为1，就是其本身的那一类
    }
    for(int i=1;i<=n;i++)
        for(int j=1;j<i;j++)
        {
            if(a[i]>a[j])
            f[i]=max(f[i],f[j]+1);
        }
    int res=0;
    for(int i=1;i<=n;i++)
    if(f[i]>res)res=f[i];
    cout<<res<<endl;
}

区间DP

石子合并

状态表示思路：$f[i][j]$表示所有第i堆石子到第j堆石子的合并方式里的代价最小值
状态计算思路：以第i到第j中任意一处的分界线来分类，先将分界线左边的石子合并，再将分界线右边的石子合并，再将左右两堆合并
代码思路:先枚举区间长度，再枚举左端点，再枚举分界线

# include 
using namespace std;
const int N=310;
int f[N][N];
int s[N];
int main()
{
    int n,temp;
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>temp;
        s[i]=s[i-1]+temp;
    }
    for(int len=2;len<=n;len++)//枚举区间长度
        for(int i=1;i+len-1<=n;i++)//枚举左端点
            {
                int l=i,r=i+len-1;//确定左右端点
                 f[l][r]=1e9;//先将f[l][r]赋一个较大的数，否则因为f[l][r]是全局变量，在后面比较min时都是0
                for(int k=l;k<=r-1;k++)
                {
                    
                    f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+s[r]-s[l-1]);
                }
            }
    cout<<f[1][n]<<endl;
}

最优二叉搜索树

类似于矩阵链乘法问题

问题的定义

给定二叉树的叶子节点和非叶节点，并给出每个节点被搜索的概率，求如何构造二叉树使树的期望搜索代价最小

问题的解决

• 一些定义：

1. 树的期望搜索代价：
   
   每个节点所在的层数（根节点是0层）+1为该节点的深度，深度乘该节点被搜索的概率为该搜索该节点的代价，所有节点的代价之和为树的期望搜索代价

2. $E[i,j]$:包含内节点$\{k_i,k_{i+1}....k_j\}$和叶节点$\{d_{i-1},d_i....d_j\}$的最优二叉搜索树的期望搜索代价,特别地当$j=i-1$时$E[i,j]=d_i-1$

3. $w[i,j]$：${\sum }_{l=i}^j{p}_l+{\sum }_{l=i-1}^j{q}_l$，即i号到j号内节点的搜索概率+i-1号到j号叶节点的搜索概率

• 动态规划算法描述
  求解$E[i,j]$的问题可以划分为以下步骤

1. 在i号到j号内节点中找一个r号节点作为根，代价为r号内节点的搜索代价$p_r(i\le r\le j)$

2. 将求解$E[i,j]$的问题划分为两个子问题$E[i,r-1]$和$E[r+1,j]$，若$r-1=i-1$则说明此时$E[i,r-1]$只包含一个叶节点$q_{i-1}$

3. 将r号节点作为根后左子树为包含内节点$\{k_i,k_{i+1}....k_{r-1}\}$和叶节点$\{d_{i-1},d_i....d_{r-1}\}$的最优二叉搜索树，右子树为包含内节点$\{k_{r+1},k_{r+2}....k_j\}$和叶节点$\{d_r,d_{r+1}....d_j\}$的最优二叉搜索树，因为将r号节点作为了根，所以这两棵子树中的所有内节点和叶节点的深度增加1，相应的二叉树的期望搜索代价增加
   

4. 经过计算可知最后将问题分为两个子问题后最后总的期望搜索代价增加$w[i,j]$

• 证明优化子结构
  
• 递归方程
  
  
  
• 算法的伪代码