lc hot100+javase整理
4.寻找两个正序数组的中位数
- 从暴力开始:归并合并两个数组然后找到中位数
- 联想到合并有序链表,但不用完全合并,维护两个指针,只需找到中位数的下标位置就可,奇偶区分比较麻烦,空间复杂度降到了O(1)
- 给出的两个数组有序且根据时间复杂度要求,需要二分查找。
【第k小数解法】
找两个有序数组中第(m+n)/2或 (m+n)/2+1小的数。
设要找第 k 小数,我们可以每次循环排除掉 k/2 个数,比较k/2处两个数组元素大小情况A组(B)大于等于B(A)组,都可以排除较小的那一组的前k/2个数,此时更新k=k-k/2,继续循环,比较更新后AB两组k/2处元素大小情况,直到K=1,两组首元素较小的那个就是目标数
边界条件:
数组为空ork为一的情况
归并排序
class Test {
public static void main(String[] args) {
Test t = new Test();
int[] nums = {3, 4, 1, 5, 2, 1};
t.mergeSort(nums, 0, nums.length - 1);
}
public void mergeSort(int[] nums, int l, int r) {
// 终止条件
if (l >= r) return;
// 递归划分
int m = (l + r) / 2;
mergeSort(nums, l, m);
mergeSort(nums, m + 1, r);
// 合并子数组
int[] tmp = new int[r - l + 1]; // 暂存需合并区间元素
for (int k = l; k <= r; k++)
tmp[k - l] = nums[k];
int i = 0, j = m - l + 1; // 两指针分别指向左/右子数组的首个元素
for (int k = l; k <= r; k++) { // 遍历合并左/右子数组
if (i == m - l + 1)
nums[k] = tmp[j++];
else if (j == r - l + 1 || tmp[i] <= tmp[j])
nums[k] = tmp[i++];
else {
nums[k] = tmp[j++];
}
}
}
}
32. 最长有效括号【栈】
读清题意,是”子串”的概念,所以有子结构,注意连续性。用栈动态维护「最后一个没有被匹配的右括号的下标」
84. 柱状图中最大的矩形
同42用栈,要搞清楚每个柱子的最大矩形的含义
42. 接雨水【栈】
- 按列来计算:左右两侧最高的柱子中偏矮的-本列高度
- dp备忘录优化:因为左右寻找最大值有重复,添加备忘录
- dp双指针:递推累加每个柱子的储水高度时只用到了 dp[i][0]和 dp[i][1] 两个值。 leftmax从左往右更新,rightmax从右往左更新。将空间复杂度从 O(N) 优化成了 O(1)。
- 单调栈:单调栈带图题解
49. 字母异位词分组
对异位词sort后都是相同的
- List
- toCharArray
- map.get().add()
- 注意kv
class Solution {
public List<List<String>> groupAnagrams(String[] strs) {
HashMap<String,ArrayList<String>> map=new HashMap<>();
for(String s:strs){
char[] ch=s.toCharArray();
Arrays.sort(ch);
String key=String.valueOf(ch);
if(!map.containsKey(key)) map.put(key,new ArrayList<>());
// map.get("x")得到的是一个List类型的集合
map.get(key).add(s);
}
return new ArrayList(map.values());
}
}
56. 合并区间
- 先按照区间起始位置排序 (java8),遍历区间再进行 n−1 次 两两合并。
Arrays.sort(intervals, (v1, v2) -> v1[0] - v2[0]); - 比较关键是看一个区间终止位置与下一个区间的起始位置大小比较,小于合并,大于直接放入结果数组
- 数组的大小会发生变化 用Arrays.copyof(res,大小)方法
class Solution {
public int[][] merge(int[][] intervals) {
// 先按照区间起始位置排序
Arrays.sort(intervals, (v1, v2) -> v1[0] - v2[0]);
// 遍历区间
int[][] res = new int[intervals.length][2];
int idx = -1;
for (int[] interval: intervals) {
// 如果结果数组是空的,或者当前区间的起始位置 > 结果数组中最后区间的终止位置,
// 则不合并,直接将当前区间加入结果数组。
if (idx == -1 || interval[0] > res[idx][1]) {
res[++idx] = interval;
} else {
// 反之将当前区间合并至结果数组的最后区间
res[idx][1] = Math.max(res[idx][1], interval[1]);
}
}
//数组的大小会发生变化
return Arrays.copyOf(res, idx + 1);
}
}
62. 不同路径 64. 最小路径和
同类型基础类型dp
3X7
1111111
1
1
1 1 1 1 1 1 1
1 2 3 4 5 6 7
1 3 6 10 15 21 28 则有28种
85、最大矩形
面试题 17.24. 最大子矩阵 二维转一维
1、一看到矩形就想着前缀和,但具体实现没有很好的思路
一个比较清晰的前缀和思路,写好前缀和数组就纯遍历。注意处理方法
官解的图 基于柱状图题的优化
2、单调栈思路
148. 排序链表[很经典很重要]
归并!!在 O(n log n) 时间复杂度和常数级空间复杂度下
数组使用归并时是 O(N)的,需要复制出相等的空间来进行赋值归并。对于链表,实际上是可以实现常数空间占用的(链表的归并排序不需要额外的空间)。递归地将当前链表分为两段,然后merge。
分两段用快慢指针的方法。
merge时,把两段头部节点值比较,用一个 p 指向较小的,且记录第一个节点,然后两段的头一步一步向后走,p也一直向后走,总是指向较小节点,直至其中一个头为NULL,处理剩下的元素。最后返回记录的头即可。
class Solution{
public ListNode sortList(ListNode head){
if(head==null||head.next==null)
return head;
ListNode fast=head.next,slow=head;
while(fast!=null && fast.next!=null){
slow=slow.next;
fast=fast.next.next;
}
ListNode tmp=slow.next;
slow.next=null;
ListNode left=sortList(head);
ListNode right=sortList(tmp);
ListNode dummyHead=new ListNode(0);
ListNode cur=dummyHead;
while(left!=null && right!=null){
if(left.val<right.val){
dummyHead.next=left;
left=left.next;
}
else{
dummyHead.next=right;
right=right.next;
}
dummyHead=dummyHead.next;
}
dummyHead.next = left != null ? left : right;//左链/右链有剩下的?赋给
return cur.next;
}
}
152. 乘积最大子数组
需要记录最大值和最小值,遇到负数最小的变最大的,最大的变最小的
207. 课程表(DAG图判断—拓扑排序,邻接矩阵的建立)
1、广度优先
- 课程前置条件列表 prerequisites 可以得到课程安排图的
- 邻接表 adjacency 课程安排构成的图是否有环,有环则不成立。
- 入度表的建立 indegrees[cp[1]]++;
- 邻接表的创建1→(2,4)、2→(3,4)……
class Solution {
public boolean canFinish(int numCourses, int[][] prerequisites) {
int[] indegrees=new int [numCourses];
List<List<Integer>> adjacency=new ArrayList<>();
Queue<Integer> queue=new LinkedList<>();
for(int i=0;i<numCourses;i++){
adjacency.add(new ArrayList<>());
}
for(int[] cp:prerequisites){
indegrees[cp[0]]++;
adjacency.get(cp[1]).add(cp[0]);
}
for(int i=0;i<numCourses;i++){
if(indegrees[i]==0) queue.add(i);
}
while(!queue.isEmpty()){
int pre=queue.poll();
numCourses--;
for(int cur:adjacency.get(pre)){
if(--indegrees[cur]==0) queue.add(cur);
}
}
return numCourses==0;
}
}
2、深度优先
通过dfs判断是否有环
三种状态设置:
0 还未被访问
1 本轮中已被访问
-1 之前轮次中已经被访问过了
对numCourses中的节点依次进行访问
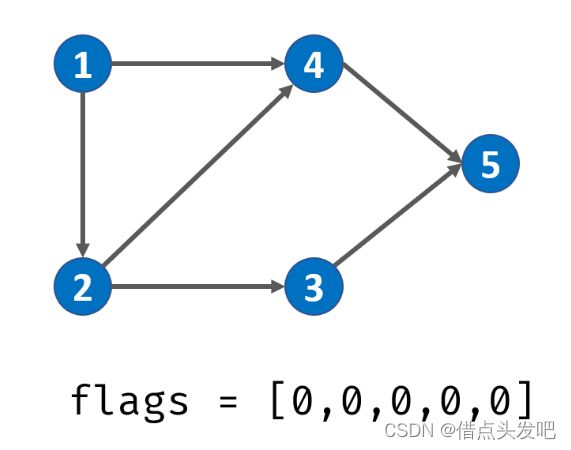
起始状态flags=0 0 0 0 0
- 第一轮从1开始 1 2 3 5 ——1 1 1 0 1,本轮结束,无环,将前置节点赋-1,以后就不需要再访问了,变为1 1 -1 0 -1
- 第二轮从2开始(2在上一轮中提前初始化为1了)2 4 ——1 1 -1 1 -1,本轮结束,无环,前置节点赋-1,变为1 1 -1 -1 -1
- 回到2 此时1-2和1-4为1,第三四轮分别赋-1
- 遍历结束,无环,返回true
邻接表:1【2,4】 2【3,4】3【5】4【5】
从1开始1-2-3-5,无环
从2开始2-4(3在上一步已经访问过了)-5 ,无环
有环的情况:1【2,4】 2【3,4】3【5】4【5】5【3】
从1开始1-2-3-5-3 其中5-3,5返回到3发现3此时为1,表示3在此轮中已经被访问过,有环,直接返回false截断,结束。
class Solution {
public boolean canFinish(int numCourses, int[][] prerequisites) {
List<List<Integer>> adjacency = new ArrayList<>();
for(int i = 0; i < numCourses; i++)
adjacency.add(new ArrayList<>());
int[] flags = new int[numCourses];
for(int[] cp : prerequisites)
adjacency.get(cp[1]).add(cp[0]);
for(int i = 0; i < numCourses; i++)
if(!dfs(adjacency, flags, i)) return false;
return true;
}
private boolean dfs(List<List<Integer>> adjacency, int[] flags, int i) {
if(flags[i] == 1) return false;
if(flags[i] == -1) return true;
flags[i] = 1;
for(Integer j : adjacency.get(i))
if(!dfs(adjacency, flags, j)) return false;
flags[i] = -1;
return true;
}
}
208. 实现 Trie (前缀树)
前(后)缀树的建立以及变式、应用!!!!
238. 除自身以外数组的乘积(前缀积x后缀积)
res[i]处的值由其左右两侧总贡献得来
- eg:[1 2 3 4],2处的res应该为1×3×4,即该位置的总贡献由左侧1,右侧3、4相乘得来
- 首先从左往右计算左贡献
- 对于1,没有左贡献。对于2,左贡献只有1。对于3,左贡献1×2=2、对于4,左贡献1×2×3=6
- 此时在左贡献1 1 2 6基础上从右往左累乘该位置的右贡献
- 对于4,没有右贡献,为6。对于3,右贡献2×4=8。对于2,右贡献4×3=12,对于1,右贡献4×3×2=24
则为24 12 8 6
class Solution {
public int[] productExceptSelf(int[] nums) {
int[] ans=new int [nums.length];
int left=1;
for(int i=0;i<nums.length;++i){
ans[i]=left;
left*=nums[i];
}
int right=1;
for(int i=nums.length-1;i>=0;--i){
ans[i]*=right;
right*=nums[i];
}
return ans;
}
}
215. 数组中的第K个最大元素(快排!快速选择模板再不会就算了)
class Solution {
int[] nums;
int qselect(int l, int r, int k) {
if (l == r) return nums[k];
int x = nums[l], i = l - 1, j = r + 1;
while (i < j) {
do i++; while (nums[i] < x);
do j--; while (nums[j] > x);
if (i < j) swap(i, j);
}
if (k <= j) return qselect(l, j, k);
else return qselect(j + 1, r, k);
}
void swap(int i, int j) {
int c = nums[i];
nums[i] = nums[j];
nums[j] = c;
}
public int findKthLargest(int[] _nums, int k) {
nums = _nums;
int n = nums.length;
return qselect(0, n - 1, n - k);
}
}
6285. 执行 K 次操作后的最大分数(327周赛 优先队列模拟)
Math.ceil(val) 向上取整函数
public long maxKelements(int[] nums, int k) {
PriorityQueue<Integer> queue=new PriorityQueue<>((a,b)->(b-a));
for(int n:nums){
queue.add(n);
}
long sum=0;
for(int i=0;i<k;i++){
int tmp=queue.poll();
sum+=tmp;
queue.add((int)Math.ceil(tmp/3.0));
}
return sum;
}
647. 回文子串(DP、双指针中心扩展、暴力)
暴力 双重循环
DP思路
class Solution {
public int countSubstrings(String s) {
int res=0;
for(int l=0;l<s.length();l++){
for(int r=l;r<s.length();r++){
res+=isPalindrome(s.substring(l,r+1));
}
}
return res;
}
int isPalindrome(String s){
char[] ch=s.toCharArray();
int i=0,j=s.length()-1;
while(i<j){
if(ch[i]!=ch[j]) return 0;
i++;
j--;
}
return 1;
}
}
406. 根据身高重建队列(sort重写)
class Solution {
public int[][] reconstructQueue(int[][] people) {
Arrays.sort(people,(a,b)->{
// 身高从大到小排(身高相同k小的站前面)
// 先按照h维度的身高顺序从高到低排序。确定第一个维度
if(a[0]==b[0]) return a[1]-b[1];
return b[0]-a[0];
});
// 根据每个元素的第二个维度k,贪心算法,进行插入
LinkedList<int[]> que=new LinkedList<>();
for(int[]p :people){
que.add(p[1],p);
}
return que.toArray(new int[people.length][]);
}
}
2536. 子矩阵元素加 1(二维差分前缀和)
一维原数组:8 2 6 3 1
维护一维差分数组:8 -6 4 -3 -2
差分:(存储前后变化量的)
对原数组i-j(1-3)内均加三即对差分数组i处+3,j+1处-3,处理过的差分数组变为:8 -3 4 -6 -2
求差分数组的前缀和即还原数组:8 5 9 3 1
可以看到的确是在原数组的基础上在(i,j)区间内+3
本题一维情况:
已知一维原数组
维护一维差分数组
对差分数组(记录变化量数组)的起始和结尾+1处+1
再对差分数组求前缀和,就可以还原数组,得到的在原数组基础上全部加一的数组。
本题为推广到二维的情况:
二维原数组:
维护二维差分数组(记录变化量的二维数组):如何记录变化量?将矩阵的第[i][j]的单元格+x操作,则此矩阵求前缀和后,其右下所有部分均加一。
那如何规定指定范围的二维变化量?
从二维前缀和的角度来看,对区域左上角 +1 会对所有右下位置产生影响,那么在区域右上角的右边相邻处和左下角的下边相邻处 −1 可以消除这个影响,但是两个 −1 又会对区域右下角的右下所有位置产生影响,所以要在右下角的右下相邻处再
+1还原回来。
最后再求前缀和,即可得到最终指定范围内+x的答案。
暴力:
class Solution{
public int[][] rangeAddQueries(int n,int[][] queries)z{
int[][] matrix=new int[n][n];
for(int[] query:queries){
int x1=query[0],y1=query[1];
int x2=query[2],y2=query[3];
matrix[x1][y1]++;
if(y2+1)
}
}
}
class Solution {
public int[][] rangeAddQueries(int n, int[][] queries) {
int[][] diff = new int[n + 2][n + 2];
for (int[] query : queries) {
int r1 = query[0] + 1, c1 = query[1] + 1;
int r2 = query[2] + 2, c2 = query[3] + 2;
diff[r1][c1]++;
diff[r1][c2]--;
diff[r2][c1]--;
diff[r2][c2]++;
}
for (int i = 1; i < n + 1; i++)
for (int j = 1; j < n + 1; j++)
diff[i][j] = diff[i][j] + diff[i - 1][j] + diff[i][j - 1] - diff[i - 1][j - 1];
int[][] ans = new int[n][n];
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
ans[i][j] = diff[i + 1][j + 1];
return ans;
}
}
dp中的滚动数组
二维数组举例
int i, j, d[100][100];
for(i = 1; i < 100; i++)
for(j = 0; j < 100; j++)
d[i][j] = d[i - 1][j] + d[i][j - 1];
上面的d[i][j]只依赖于d[i - 1][j], d[i][j - 1];
运用滚动数组
int i, j, d[2][100];
for(i = 1; i < 100; i++)
for(j = 0; j < 100; j++)
d[i % 2][j] = d[(i - 1) % 2][j] + d[i % 2][j - 1];
根据「转移方程」,我们知道计算第 行格子只需要第 行中的某些值。
也就是计算「某一行」的时候只需要依赖「前一行」。
因此可以用一个只有两行的数组来存储中间结果,根据当前计算的行号是偶数还是奇数来交替使用第 0 行和第 1 行。

