愤怒的导数：一点可导和邻域内可导能推出来什么？

愤怒的导数：一点可导和邻域内可导能推出来什么？

一、连续和可导的基本概念

01 连续的定义

设函数 $y=f(x)$ 在点 $x_0$ 的某一邻域内有定义，如果满足以下条件：
$$\underset{\Delta x\to 0}{\lim }\Delta y=\underset{\Delta x\to 0}{\lim }\left[f\left(x_0+\Delta x\right)-f\left(x_0\right)\right]=0或\underset{x\to x_0}{\lim }f(x)=f\left(x_0\right)$$
那么就称函数 $y=f(x)$ 在点 $x_0$ 连续；否则称 $f(x)$ 在点 $x_0$ 间断。

即函数在某点连续的充要条件是该点左极限右极限存在且相等并且等于该点函数值。

02 可导的定义

设函数 $y=f(x)$ 在点 $x_0$ 的某邻域内有定义，当自变量 $x$ 在 $x_0$ 处有增量 $\Delta x$ ( $x_0+\Delta x$ 点仍在该邻域内 )，

函数相应地有增量 $\Delta y=f\left(x_0+\Delta x\right)-f\left(x_0\right)$，则有：
$$f^{\prime }\left(x_0\right)\stackrel{def}{=}\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0}{\lim }\frac{f\left(x_0+\Delta x\right)-f\left(x_0\right)}{\Delta x}=\underset{x\to x_0}{\lim }\frac{f(x)-f\left(x_0\right)}{x-x_0}$$
如果极限存在，则称函数 $y=f(x)$ 在点 $x_0$ 处可导，此极限值称为函数 $y=f(x)$ 在点 $x_0$ 处的导数 ( 微商 ) 。

补充：二阶可导的定义

设函数 $y=f(x)$ 在点 $x_0$ 的某邻域 $U_{\delta }\left(x_0\right)$ 内有一阶导数 ( $f^{\prime }(x)$ 在点 $x_0$ 的某邻域内有定义 ) 。如果极限

$\underset{\Delta x\to 0}{\lim }\frac{f^{\prime }\left(x_0+\Delta x\right)-f^{\prime }\left(x_0\right)}{\Delta x}=\underset{x\to x_0}{\lim }\frac{f^{\prime }(x)-f^{\prime }\left(x_0\right)}{x-x_0}$ 存在，则称函数 $y=f(x)$ 在点 $x_0$ 处二阶可导，

即 $f^{\prime }(x)$ 在 $x_0$ 处一阶可导。此极限值称为函数 $y=f(x)$ 在点 $x_0$ 处的二阶导数，记为 $f^{\prime \prime }\left(x_0\right)$ 。

二、连续作为条件

01 某点连续

$$f(x)\text{ 在 }{x}_0\text{ 连续 }\Rightarrow \{\begin{array}{l}\text{ 1. }f(x)\text{ 在 }{x}_0\text{ 邻域内有定义 }✅\\ \text{ 2. }\underset{x\to x_0}{\lim }f(x)=f\left(x_0\right)✅\\ \text{ 3. }f(x)\text{ 在 }{x}_0\text{ 邻域内连续 }❌\\ \text{ 4. }f(x)\text{ 在 }{x}_0\text{ 可导 }❌\end{array}$$

02 某邻域内连续

$$f(x)\text{ 在 }{x}_0\text{ 某邻域 }{U}_{\delta }\left(x_0\right)\text{ 内连续 }\Rightarrow \{\begin{array}{l}1.f(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 邻域内有定义 }✅\\ 2.f(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 邻域内处处连续 }✅\\ 3.f(x)\text{ 在 }{x}_0\text{ 可导 }❌\end{array}$$

03 某去心邻域内连续

$$f(x)\text{ 在 }{x}_0\text{ 去心邻域 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内连续 }\Rightarrow \{\begin{array}{l}\text{ 1. }f(x)\text{ 在去心邻域 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内有定义 }✅\\ \text{ 2. }f(x)\text{ 在去心邻域 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内处处连续 }✅\\ \text{ 3. }f(x)\text{ 在 }{x}_0\text{ 极限存在 }❌\\ \text{ 4. }f(x)\text{ 在 }{x}_0\text{ 可导 }❌\end{array}$$

三、可导作为条件

01 某点可导

$$f(x)\text{ 在 }{x}_0\text{ 可导 }\Rightarrow \{\begin{array}{l}\text{ 1. }{f}^{\prime }(x)\text{ 在 }{x}_0\text{ 有定义 }✅\\ \text{ 2. }{f}_{-}^{\prime }(x)=f_{+}^{\prime }(x)✅\\ \text{ 3. }f(x)\text{ 在 }{x}_0\text{ 连续 }✅\\ \text{ 4. }f(x)\text{ 在 }{x}_0\text{ 邻域内连续 }❌\\ \text{ 5. }f(x)\text{ 在 }{x}_0\text{ 邻域内可导 }❌\end{array}$$

02 某邻域内可导

$$f(x)\text{ 在 }{x}_0\text{ 某邻域 }{U}_{\delta }\left(x_0\right)\text{ 内可导 }\Rightarrow \{\begin{array}{l}1.f(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 内连续 }✅\\ \text{ 2. }f(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 内极限存在 }✅\\ \text{ 3. }f(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 内有定义 }✅\\ \text{ 4. }{f}^{\prime }(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 内连续 }❌\\ \text{ 5. }{f}^{\prime }(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 内极限存在 }❌\\ \text{ 6. }{f}^{\prime }(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 内有定义 }✅\end{array}$$

03 某去心邻域内可导

$$f(x)\text{ 在 }{x}_0\text{ 去心邻域 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内可导 }\Rightarrow \{\begin{array}{l}\text{ 1. }{f}^{\prime }(x)\text{ 在 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内有定义 }✅\\ \text{ 2. }f(x)\text{ 在 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内连续 }✅\\ \text{ 3. }f(x)\text{ 在 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内极限存在 }✅\\ \text{ 4. }{f}^{\prime }(x)\text{ 在 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内有定义 }✅\\ \text{ 5. }f(x)\text{ 在 }{x}_0\text{ 有定义 }❌\\ \text{ 6. }f(x)\text{ 在 }{x}_0\text{ 连续 }❌\\ \text{ 7. }f(x)\text{ 在 }{x}_0\text{ 极限存在 }❌\\ \text{ 8. }f(x)\text{ 在 }{x}_0\text{ 有定义 }❌\end{array}$$

四、命题不成立的反例

• $f(x)\text{ 在 }{x}_0\text{ 连续 }\nRightarrow f(x)\text{ 在 }{x}_0\text{ 邻域内连续 }$
  $$\begin{array}{rl}& f(x)=\{\begin{array}{l}x,\text{ 当 }x\text{ 为有理数; }\\ 0,\text{ 当 }x\text{ 为无理数. }\end{array}=x\cdot D(x),\\ & 其中D(x)为狄利克雷函数:D(x)=\{\begin{array}{l}1,x\text{ 为有理数; }\\ 0,x\text{ 为无理数. }\end{array}\\ & \underset{x\to 0}{\lim }f(x)=\underset{x\to 0}{\lim }[xD(x)]=0=f(0),从而f(x)在x=0处连续.\\ & 但如果在x_0\ne 0处,选择不同的路径:\\ & (1)x\to x_0时选择有理数路径,则\underset{x\to x_0}{\lim }f(x)=x_0,\\ & (2)x\to x_0时选择无理数路径,则\underset{x\to x_0}{\lim }f(x)=0.\\ & 所以\underset{x\to x_0}{\lim }f(x)不存在,从而f(x)在x_0\ne 0处不连续.\end{array}$$

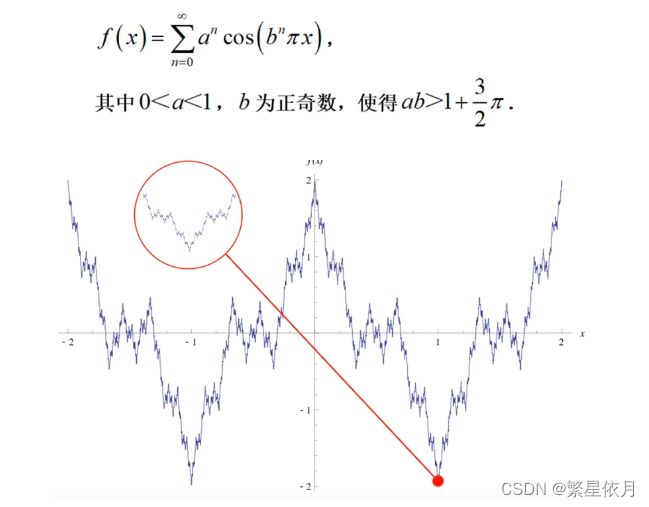
• $f(x)\text{ 在 }{x}_0\text{ 某邻域 }{U}_{\delta }\left(x_0\right)\text{ 内连续 }\nRightarrow f(x)\text{ 在 }{x}_0\text{ 可导 }$

  处处连续但处处不可导：维尔斯特拉斯函数

  

• 可导是光滑的充分不必要条件

  处处光滑不一定处处可导

  

• $f(x)\text{ 在 }{x}_0\text{ 可导 }\nRightarrow f(x)\text{ 在 }{x}_0\text{ 邻域内连续 }$

  一点可导推不出邻域内连续。
  $$\begin{array}{rl}& f(x)=\{\begin{array}{l}{x}^2,x\text{ 为有理数 }\\ 0,x\text{ 为无理数}\end{array}=x^2\cdot D(x)，\\ & 其中D(x)为狄利克雷函数:D(x)=\{\begin{array}{l}1,x\text{ 为有理数 }\\ 0,x\text{ 为无理数 }\end{array}\\ & f^{\prime }(0)=\underset{x\to 0}{\lim }\frac{f(x)-f(0)}{x-0}=\underset{x\to 0}{\lim }\frac{x^{2}D(x)}{x}=\underset{x\to 0}{\lim }[xD(x)]=0.\\ & \underset{x\to 0}{\lim }f(x)=\underset{x\to 0}{\lim }\left[x^{2}D(x)\right]=0=f(0)，从而f(x)在x=0连续。\\ & 但在其他点，均为间断点，不连续。\end{array}$$

• $f(x)\text{ 在 }{x}_0\text{ 某邻域 }{U}_{\delta }\left(x_0\right)\text{ 内可导 }\nRightarrow f^{\prime }(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 内连续 }$

  $f(x)\text{ 在 }{x}_0\text{ 某邻域 }{U}_{\delta }\left(x_0\right)\text{ 内可导 }\nRightarrow f^{\prime }(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 内极限存在 }$

  邻域内处处可导，但导函数不连续，极限不存在。
  $$\begin{array}{rl}& f(x)=\{\begin{array}{c}{x}^2\sin \frac{1}{x},x\ne 0\\ 0,x=0\end{array}，f(x)在R上处处可导，但f^{\prime }(x)不连续，有振荡间断点。\\ & f^{\prime }(0)=\underset{x\to 0}{\lim }\frac{f(x)-f(0)}{x-0}=\underset{x\to 0}{\lim }\frac{x^2\sin \frac{1}{x}}{x}=\underset{x\to 0}{\lim }x\sin \frac{1}{x}=0\\ & x\ne 0时，f^{\prime }(x)=2x\sin \frac{1}{x}-\cos \frac{1}{x}，所以f^{\prime }(x)=\{\begin{array}{l}2x\sin \frac{1}{x}-\cos \frac{1}{x},x\ne 0\\ 0,x=0\end{array}\\ & 但\underset{x\to 0}{\lim }{f}^{\prime }(x)=\underset{x\to 0}{\lim }\left(2x\sin \frac{1}{x}-\cos \frac{1}{x}\right)不存在，从而f^{\prime }(x)在x=0处不连续。\end{array}$$

五、概念判断练习

如果 $f(x)$ 在 $x_0$ 二阶可导，判断以下命题是否正确。

1. $f^{\prime \prime }(x)$ 在 $x_0$ 可导。❌

2. $f^{\prime \prime }(x)$ 在 $x_0$ 连续。❌

3. $f^{\prime \prime }(x)$ 在 $x_0$ 有定义。✅

4. $\underset{x\to x_0}{\lim }{f}^{\prime \prime }(x)$ 存在。❌

5. $f^{\prime }(x)$ 在 $x_0$ 可导。✅

6. $f^{\prime }(x)$ 在 $x_0$ 连续。✅

7. $f^{\prime }(x)$ 在 $x_0$ 有定义。✅

8. $\underset{x\to x_0}{\lim }{f}^{\prime }(x)$ 存在。✅

9. $f(x)$ 在 $x_0$ 可导。✅

10. $f(x)$ 在 $x_0$ 连续。✅

11. $f(x)$ 在 $x_0$ 有定义。✅

12. $\underset{x\to x_0}{\lim }f(x)$ 存在。✅

13. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。❌

14. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。❌

15. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内有定义。❌

16. $\underset{x\to t}{\lim }{f}^{\prime \prime }(x)$ 存在, $t\in U_{\delta }\left(x_0\right)$。❌

17. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。❌

18. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。❌

19. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内有定义。✅

20. $\underset{x\to t}{\lim }{f}^{\prime }(x)$ 存在, $t\in U_s\left(x_0\right)$。❌

21. $f(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。✅

22. $f(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。✅

23. $f(x)$ 在 $x_0$ 邻域 $U_s\left(x_0\right)$ 内有定义。✅

24. $\underset{x\to t}{\lim }f(x)$ 存在，$t\in U_{\delta }(x)$ 。✅

如果 $f(x)$ 在 $x_0$ 的邻域 $U_{\delta }(x_0)$ 内二阶可导，判断以下命题是否正确。

1. $f^{\prime \prime }(x)$ 在 $x_0$ 可导。❌
2. $f^{\prime \prime }(x)$ 在 $x_0$ 连续。❌
3. $f^{\prime \prime }(x)$ 在 $x_0$ 有定义。✅
4. $\underset{x\to x_0}{\lim }{f}^{\prime \prime }(x)$ 存在。❌
5. $f^{\prime }(x)$ 在 $x_0$ 可导。✅
6. $f^{\prime }(x)$ 在 $x_0$ 连续。✅
7. $f^{\prime }(x)$ 在 $x_0$ 有定义。✅
8. $\underset{x\to x_0}{\lim }{f}^{\prime }(x)$ 存在。✅
9. $f(x)$ 在 $x_0$ 可导。✅
10. $f(x)$ 在 $x_0$ 连续。✅
11. $f(x)$ 在 $x_0$ 有定义。✅
12. $\underset{x\to x_0}{\lim }f(x)$ 存在。✅
13. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。❌
14. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。❌
15. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内有定义。✅
16. $\underset{x\to t}{\lim }{f}^{\prime \prime }(x)$ 存在, $t\in U_{\delta }\left(x_0\right)$。❌
17. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。✅
18. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。✅
19. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内有定义。✅
20. ${\lim }_{x\to t}{f}^{\prime }(x)$ 存在, $t\in U_s\left(x_0\right)$。✅
21. $f(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。✅
22. $f(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。✅
23. $f(x)$ 在 $x_0$ 邻域 $U_s\left(x_0\right)$ 内有定义。✅
24. $\underset{x\to t}{\lim }f(x)$ 存在，$t\in U_{\delta }(x)$ 。✅

如果 $f(x)$ 在 $x_0$ 的去心邻域 $U_{\delta }(x_0)$ 内二阶可导，判断以下命题是否正确。

1. $f^{\prime \prime }(x)$ 在 $x_0$ 可导。❌

2. $f^{\prime \prime }(x)$ 在 $x_0$ 连续。❌

3. $f^{\prime \prime }(x)$ 在 $x_0$ 有定义。❌

4. $\underset{x\to x_0}{\lim }{f}^{\prime \prime }(x)$ 存在。❌

5. $f^{\prime }(x)$ 在 $x_0$ 可导。❌

6. $f^{\prime }(x)$ 在 $x_0$ 连续。❌

7. $f^{\prime }(x)$ 在 $x_0$ 有定义。❌

8. $\underset{x\to x_0}{\lim }{f}^{\prime }(x)$ 存在。❌

9. $f(x)$ 在 $x_0$ 可导。❌

10. $f(x)$ 在 $x_0$ 连续。❌

11. $f(x)$ 在 $x_0$ 有定义。❌

12. $\underset{x\to x_0}{\lim }f(x)$ 存在。❌

13. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。❌

14. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。❌

15. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内有定义。✅

16. $\underset{x\to t}{\lim }{f}^{\prime \prime }(x)$ 存在, $t\in U_{\delta }\left(x_0\right)$。❌

17. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。✅

18. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。✅

19. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内有定义。✅

20. $\underset{x\to t}{\lim }{f}^{\prime }(x)$ 存在, $t\in U_s\left(x_0\right)$。✅

21. $f(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。✅

22. $f(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。✅

23. $f(x)$ 在 $x_0$ 邻域 $U_s\left(x_0\right)$ 内有定义。✅

24. $\underset{x\to t}{\lim }f(x)$ 存在，$t\in U_{\delta }(x)$ 。✅

如果 $f(x)$ 在 $x=x_0$ 处存在一阶连续导数，判断以下命题是否正确。

1. $f(x)$ 在 $x_0$ 处可导。✅
2. $f(x)$ 在 $x_0$ 的去心邻域内可导。✅
3. $f^{\prime }(x)$ 在 $x_0$ 处连续。✅
4. $f^{\prime }(x)$ 在 $x_0$ 的去心邻域内连续。

如果 $f(x)$ 在 $x=x_0$ 处存在二阶导数，判断以下命题是否正确。

1. $f(x)$ 在 $x_0$ 处可导。✅
2. $f(x)$ 在 $x_0$ 的去心邻域内可导。✅
3. $f^{\prime }(x)$ 在 $x_0$ 处连续。✅
4. $f^{\prime }(x)$ 在 $x_0$ 的去心邻域内连续。❌
5. $f(x)$ 在 $x_0$ 的去心邻域内存在二阶导数。❌

六、无答案练习纯享版

$f(x)$ 在某点连续，判断以下命题是否正确。
$$f(x)\text{ 在 }{x}_0\text{ 连续 }\Rightarrow \{\begin{array}{l}\text{ 1. }f(x)\text{ 在 }{x}_0\text{ 邻域内有定义 }\\ \text{ 2. }\underset{x\to x_0}{\lim }f(x)=f\left(x_0\right)\\ \text{ 3. }f(x)\text{ 在 }{x}_0\text{ 邻域内连续 }\\ \text{ 4. }f(x)\text{ 在 }{x}_0\text{ 可导 }\end{array}$$

$f(x)$ 在某邻域内连续，判断以下命题是否正确。
$$f(x)\text{ 在 }{x}_0\text{ 某邻域 }{U}_{\delta }\left(x_0\right)\text{ 内连续 }\Rightarrow \{\begin{array}{l}1.f(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 邻域内有定义 }\\ 2.f(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 邻域内处处连续 }\\ 3.f(x)\text{ 在 }{x}_0\text{ 可导 }\end{array}$$

$f(x)$ 在某去心邻域内连续，判断以下命题是否正确。
$$f(x)\text{ 在 }{x}_0\text{ 去心邻域 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内连续 }\Rightarrow \{\begin{array}{l}\text{ 1. }f(x)\text{ 在去心邻域 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内有定义 }\\ \text{ 2. }f(x)\text{ 在去心邻域 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内处处连续 }\\ \text{ 3. }f(x)\text{ 在 }{x}_0\text{ 极限存在 }\\ \text{ 4. }f(x)\text{ 在 }{x}_0\text{ 可导 }\end{array}$$

$f(x)$ 在某点可导，判断以下命题是否正确。
$$f(x)\text{ 在 }{x}_0\text{ 可导 }\Rightarrow \{\begin{array}{l}\text{ 1. }{f}^{\prime }(x)\text{ 在 }{x}_0\text{ 有定义 }\\ \text{ 2. }{f}_{-}^{\prime }(x)=f_{+}^{\prime }(x)\\ \text{ 3. }f(x)\text{ 在 }{x}_0\text{ 连续 }\\ \text{ 4. }f(x)\text{ 在 }{x}_0\text{ 邻域内连续 }\\ \text{ 5. }f(x)\text{ 在 }{x}_0\text{ 邻域内可导 }\end{array}$$

$f(x)$ 在某邻域内可导，判断以下命题是否正确。
$$f(x)\text{ 在 }{x}_0\text{ 某邻域 }{U}_{\delta }\left(x_0\right)\text{ 内可导 }\Rightarrow \{\begin{array}{l}1.f(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 内连续 }\\ \text{ 2. }f(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 内极限存在 }\\ \text{ 3. }f(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 内有定义 }\\ \text{ 4. }{f}^{\prime }(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 内连续 }\\ \text{ 5. }{f}^{\prime }(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 内极限存在 }\\ \text{ 6. }{f}^{\prime }(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 内有定义 }\end{array}$$

$f(x)$ 在某去心邻域内可导，判断以下命题是否正确。
$$f(x)\text{ 在 }{x}_0\text{ 去心邻域 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内可导 }\Rightarrow \{\begin{array}{l}\text{ 1. }{f}^{\prime }(x)\text{ 在 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内有定义 }\\ \text{ 2. }f(x)\text{ 在 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内连续 }\\ \text{ 3. }f(x)\text{ 在 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内极限存在 }\\ \text{ 4. }{f}^{\prime }(x)\text{ 在 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内有定义 }\\ \text{ 5. }f(x)\text{ 在 }{x}_0\text{ 有定义 }\\ \text{ 6. }f(x)\text{ 在 }{x}_0\text{ 连续 }\\ \text{ 7. }f(x)\text{ 在 }{x}_0\text{ 极限存在 }\\ \text{ 8. }f(x)\text{ 在 }{x}_0\text{ 有定义 }\end{array}$$

如果 $f(x)$ 在 $x_0$ 二阶可导，判断以下命题是否正确。

1. $f^{\prime \prime }(x)$ 在 $x_0$ 可导。

2. $f^{\prime \prime }(x)$ 在 $x_0$ 连续。

3. $f^{\prime \prime }(x)$ 在 $x_0$ 有定义。

4. $\underset{x\to x_0}{\lim }{f}^{\prime \prime }(x)$ 存在。

5. $f^{\prime }(x)$ 在 $x_0$ 可导。

6. $f^{\prime }(x)$ 在 $x_0$ 连续。

7. $f^{\prime }(x)$ 在 $x_0$ 有定义。

8. $\underset{x\to x_0}{\lim }{f}^{\prime }(x)$ 存在。

9. $f(x)$ 在 $x_0$ 可导。

10. $f(x)$ 在 $x_0$ 连续。

11. $f(x)$ 在 $x_0$ 有定义。

12. $\underset{x\to x_0}{\lim }f(x)$ 存在。

13. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。

14. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。

15. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内有定义。

16. $\underset{x\to t}{\lim }{f}^{\prime \prime }(x)$ 存在, $t\in U_{\delta }\left(x_0\right)$。

17. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。

18. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。

19. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内有定义。

20. ${\lim }_{x\to t}{f}^{\prime }(x)$ 存在, $t\in U_s\left(x_0\right)$。

21. $f(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。

22. $f(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。

23. $f(x)$ 在 $x_0$ 邻域 $U_s\left(x_0\right)$ 内有定义。

24. $\underset{x\to t}{\lim }f(x)$ 存在，$t\in U_{\delta }(x)$ 。

如果 $f(x)$ 在 $x_0$ 的邻域 $U_{\delta }(x_0)$ 内二阶可导，判断以下命题是否正确。

1. $f^{\prime \prime }(x)$ 在 $x_0$ 可导。
2. $f^{\prime \prime }(x)$ 在 $x_0$ 连续。
3. $f^{\prime \prime }(x)$ 在 $x_0$ 有定义。
4. $\underset{x\to x_0}{\lim }{f}^{\prime \prime }(x)$ 存在。
5. $f^{\prime }(x)$ 在 $x_0$ 可导。
6. $f^{\prime }(x)$ 在 $x_0$ 连续。
7. $f^{\prime }(x)$ 在 $x_0$ 有定义。
8. $\underset{x\to x_0}{\lim }{f}^{\prime }(x)$ 存在。
9. $f(x)$ 在 $x_0$ 可导。
10. $f(x)$ 在 $x_0$ 连续。
11. $f(x)$ 在 $x_0$ 有定义。
12. $\underset{x\to x_0}{\lim }f(x)$ 存在。
13. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。
14. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。
15. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内有定义。
16. $\underset{x\to t}{\lim }{f}^{\prime \prime }(x)$ 存在, $t\in U_{\delta }\left(x_0\right)$。
17. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。
18. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。
19. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内有定义。
20. ${\lim }_{x\to t}{f}^{\prime }(x)$ 存在, $t\in U_s\left(x_0\right)$。
21. $f(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。
22. $f(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。
23. $f(x)$ 在 $x_0$ 邻域 $U_s\left(x_0\right)$ 内有定义。
24. $\underset{x\to t}{\lim }f(x)$ 存在，$t\in U_{\delta }(x)$ 。

如果 $f(x)$ 在 $x_0$ 的去心邻域 $U_{\delta }(x_0)$ 内二阶可导，判断以下命题是否正确。

1. $f^{\prime \prime }(x)$ 在 $x_0$ 可导。

2. $f^{\prime \prime }(x)$ 在 $x_0$ 连续。

3. $f^{\prime \prime }(x)$ 在 $x_0$ 有定义。

4. $\underset{x\to x_0}{\lim }{f}^{\prime \prime }(x)$ 存在。

5. $f^{\prime }(x)$ 在 $x_0$ 可导。

6. $f^{\prime }(x)$ 在 $x_0$ 连续。

7. $f^{\prime }(x)$ 在 $x_0$ 有定义。

8. $\underset{x\to x_0}{\lim }{f}^{\prime }(x)$ 存在。

9. $f(x)$ 在 $x_0$ 可导。

10. $f(x)$ 在 $x_0$ 连续。

11. $f(x)$ 在 $x_0$ 有定义。

12. $\underset{x\to x_0}{\lim }f(x)$ 存在。

13. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。

14. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。

15. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内有定义。

16. $\underset{x\to t}{\lim }{f}^{\prime \prime }(x)$ 存在, $t\in U_{\delta }\left(x_0\right)$。

17. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。

18. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。

19. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内有定义。

20. $\underset{x\to t}{\lim }{f}^{\prime }(x)$ 存在, $t\in U_s\left(x_0\right)$。

21. $f(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。

22. $f(x)$ 在 $x_0$ 邻域 U δ (