Adaptive Homogeneity-DirectedDemosaicing Algorithm
Abstract
经济高效的数码相机使用单图像传感器，将红色、绿色和蓝色滤色镜的交替图案应用到每个像素位置。通过估计每个颜色平面中缺失的像素分量来重建彩色图像的完整三色表示的方法称为去马赛克算法。本文提出了通常与结合二维 (2-D) 方向插值的去马赛克算法相关的三个固有问题：误导色彩伪影、插值色彩伪影和混叠。可以使用度量邻域建模来比较两个图像中存在的误导性颜色伪影的水平。所提出的去马赛克算法通过在颜色伪影较少的方向上进行插值来估计丢失的像素。通过将滤波器组技术应用于二维方向插值来解决混叠问题。使用非线性迭代过程减少插值伪影。使用数字图像的实验结果证实了该方法的有效性。
I. INTRODUCTION
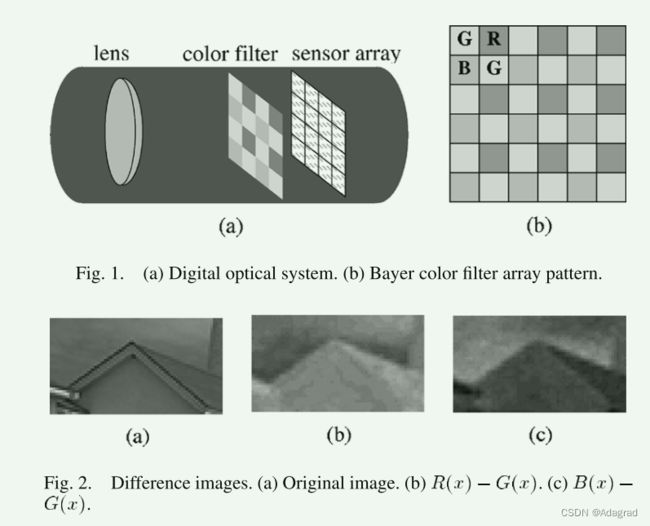
在典型的数码相机中，在图像平面上形成的光学图像由单个 CCD 或 CMOS 传感器阵列捕获[见图 1(a)]。由于传感器和镜头之间布置了彩色胶片或染料，每个单独的传感器只能捕获单一颜色。去马赛克算法是一种通过估计每个颜色平面中缺失的像素分量来重建彩色图像的完整三色表示的方法。滤色器的排列称为滤色器阵列或CFA。图 1(b) 显示了流行的拜耳模式 [2]。绿色像素以更高的速率采样，因为绿色非常接近感知亮度，并且与红色和蓝色相比，人眼对绿色更敏感。
去马赛克问题可以解释为信号插值问题。然而，简单的平面插值经常会导致颜色伪影，因为红色、绿色和蓝色的比例在对象边界处被破坏。尽管我们的视觉系统对颜色变化的敏感度不如对亮度变化的敏感度，这是一个公认的事实，但与场景完全无关的颜色表现比亮度的微小变化更引人注目。此外，由于通常情况下，在 CFA 中相似的颜色永远不会彼此相邻，因此输出图像经常会出现交替颜色的图案，通常称为拉链。也就是说，每个颜色平面对一个像素的重建的贡献与其直接相邻像素的贡献不同，因此对输出施加了人工重复模式。这种拉链人工制品的示例如图 10 所示。
通过引入彩色图像模型和利用不同颜色通道之间的结构，提出了许多算法来克服这些困难。例如，[4]和[11]使用两个颜色通道的商缓慢变化的特性。这一假设源于这样一个事实：如果两种颜色在色度平面 [16] 中占据相同的坐标，则颜色分量之间的比率相等。也就是说，令 (r1,g1)和(r2,g2) 分别为三刺激值(R1,G1,B1)和(R2,G2,B2)的色度坐标。如果(r1,g1)=(r2,g2)，那么R1/G1=R2/G2。
或者，许多人断言红色、绿色和蓝色图像之间的差异正在缓慢变化 [1]、[6]、[7]、[13]。这一原理是由于观察到颜色通道高度相关而产生的。绿色和红色（蓝色）通道之间的差异图像仅包含低频分量，因此差异图像的插值变得更容易。 [8] 中探索了一种更复杂的颜色通道相关模型。
此外，许多去马赛克算法[1]、[11]、[12]在插值中纳入了边缘方向性。对于大多数图像模型而言，沿对象边界进行插值优于跨此边界进行插值。
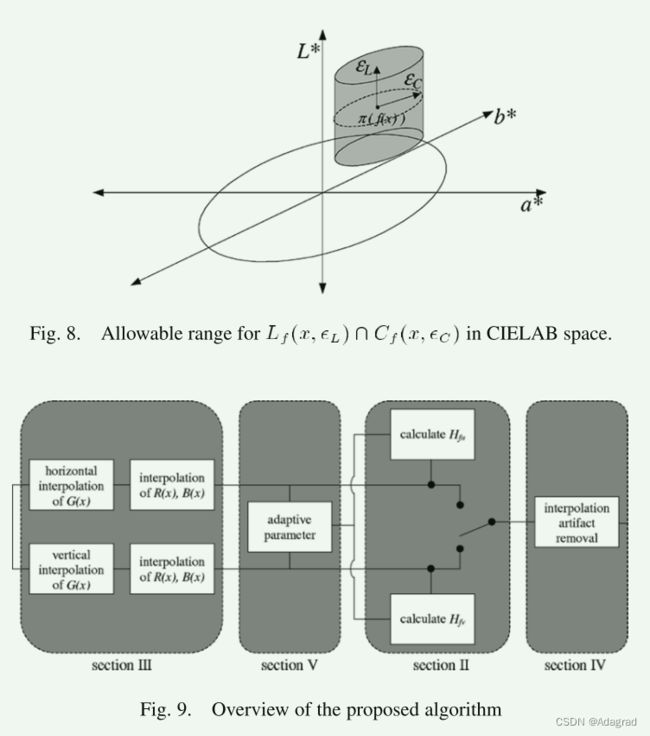
通常与结合了定向二维 (2-D) 插值的去马赛克算法相关的三个固有问题是误导性颜色伪影、插值伪影和混叠。所提出的去马赛克算法也采用定向插值方法，明确地解决了这些问题。在估计丢失像素分量的过程中，通过将滤波器组技术应用于定向插值来解决混叠问题（第二节）。该插值过程产生两个图像：水平插值图像和垂直插值图像。通过彩色图像均匀性度量来比较这些图像中存在的误导性颜色伪影的水平（第 III 节）。通过仅保持在伪影较少的方向上插值的像素，可以最大限度地减少误导性颜色伪影。使用非线性迭代过程可以减少插值伪影（第 IV 节）。通过明确地将算法设计针对伪影和混叠问题，所提出的去马赛克算法实现了输出图像质量的显着提高。
II. ALIAS AND BAYER PATTERN INTERPOLATION
设X为一组二维像素位置， Y为一组 CIE RGB 三色刺激值：则 
、 ![y=[R,G,B]^{T}](http://img.e-com-net.com/image/info8/8711f50f20ae4a7fa35b73f932feaa66.png){kind=small}
其中R、G和B分别表示红色、绿色和蓝色三色刺激值 [14]、[16]。那么彩色图像f:X->Y是像素位置和三刺激值之间的映射。
本节的目标是开发一种技术，使用分别面向水平和垂直方向的二维线性滤波器来生成从 CFA 数据插值的彩色图像fH和fV。由于矩形采样点阵，拜耳模式中水平和垂直方向的插值设计比其他方向（例如对角线）要简单得多[见图1(b)]。所提出的算法仅探讨了水平和垂直插值（有关其他讨论，请参阅第 V-A 节）。
从 CFA 数据中估计丢失像素分量的问题可以解释为从采样信号中删除混叠项。在所提出的算法中，采用滤波器组理论，通过采用红色和蓝色通道中已知像素的线性组合来消除绿色通道中的混叠项（第 II-A 节）。通过使用插值绿色通道去除高频分量来重建红色和蓝色通道（第 II-B 节）。
A. Interpolation of Green Pixel Components
在本节中，开发了一种通过水平插值进行重建G(.)的方法。垂直方向的插值也以同样的方式进行。令R(.) 、G(.) 、和B(.)分别表示红、绿、蓝彩色平面图像， 和 
。假设
缓慢变化 [1]、[6]、[7]、[13]。也就是说，差分图像的高频分量比G(x)的高频分量衰减得更快： 频率 
处的 G(x)-R(x)功率大约是相同频率下G(x)功率的五分之一。图 2 是支持这一主张的典型差异图像的示例。
本小节重点介绍使用拜耳模式的绿-红行从已知的绿色和红色像素值中估计丢失的绿色像素（见图 3）。使用相同的技术从已知的绿色和蓝色像素中估计丢失的绿色像素。在拜耳模式的绿红行中，给出了绿色图像的偶数样本和红色图像的奇数样本。给定任何信号P(x)，让P0(x)和P1(x)表示P(x)的偶数和奇数采样信号。那是
B. Interpolation ofRed/Blue Pixel Components
III. MISGUIDANCE COLOR ARTIFACTS AND HOMOGENEITY
本节的目标是开发一种方法来比较 fH和fV 中存在的色彩伪影水平。去马赛克中最大的错误来源发生在错误选择插值方向时。在本文中，我们将这种现象称为误导色彩伪影。我们将由于任何其他原因而出现的颜色伪影称为插值伪影。后面的部分将讨论减少插值伪影的方法。
误导性色彩伪影对人眼来说是令人反感的，我们有兴趣减少它们。第 III-A 节阐述了度量邻域模型和同质性图的概念。第 III-B 节描述了均匀性图和色彩伪影之间的关系。我们表明，同质性图 (13) 可用于分析和最小化误导性颜色伪影的水平。
A. Metric Neighborhood Model Review
B. Homogeneity and Artifacts
当错误地选择插值方向时，就会出现误导伪影。沿对象边界进行插值优于跨该边界进行插值，因为边界处信号的不连续性包含难以估计的高频分量。当图像沿与对象边界方向正交的方向插值时，感兴趣像素处出现的颜色与图像中表示的物理对象无关。因此，被严重颜色伪影标记的像素附近几乎没有相似的像素，并且我们假设误导性颜色伪影作为孤立事件发生。换句话说，具有颜色伪影的区域具有较小的均匀性图值 (13)。
图10清楚地说明了这一点。当使用水平方向的二维滤波器对包含垂直对象边界的图像进行插值时（如白色尖桩篱栅），在白色背景上会看到多种橙色和蓝色色块的阴影。然而，当使用垂直方向的二维滤波器对同一图像进行插值时，图像仅由白色和灰色表面组成。图11对应于图10中灯塔图像的均匀性图（这里，更亮的白色意味着更大的均匀性值）。与白色尖桩篱栅的垂直插值相对应的均匀性值明显大于水平插值的均匀性值。
很容易将这种技术推广到组合两个以上的图像；只保留其中对应均匀度图值最大的像素值。
使用方向性选择方法的去马赛克算法有时会遇到另一种类型的伪影。从一个方向插值到另一方向插值的频繁切换会导致输出图像不连续。例如，一条细的、低对比度的线可能会断成碎片，尤其是在输入数据有噪声的情况下。人眼对线条等图案很敏感，因此保护它们很重要。对均匀性图进行空间平均可以显着减少不连续性问题。换句话说，(14) 被修改为
IV. INTERPOLATION ARTIFACT REDUCTION
即使使用完美的方向选择器，插值算法的输出图像[参见（6）和（10）]也可能包含颜色伪影。在本文中，这种现象被称为插值伪影，它与插值的局限性有关。通常，插值伪影远不如误导伪影（第 III 节）那么令人反感，尽管它们仍然很明显。使用类似于[8]、[11]、[13]提出的迭代算法的非线性技术来减少插值伪影。回想一下，我们在第二节中的假设表明，差异图像 R-G和 B-G是缓慢变化的。让 median(.)表示中值滤波器算子。以下迭代过程执行m次，抑制颜色的微小变化，同时保留边缘
V. COMPLETE ALGORITHM
A. Homogeneity-Directed Demosaicing Algorithm
同质定向去马赛克算法如下。
作者没有考虑在对角线方向进行插值。虽然在水平和垂直以外的方向上进行滤波通常可能是一种有效的做法，但将对角线插值合并到同质定向去马赛克算法中需要大量的工作。在第三节中，我们声称（15）最大限度地减少了误导性的色彩伪影。 (15)的有效性取决于这样的事实：当插值方向选择错误时，颜色伪影严重并且均匀性值很小。这要求滤波系数具有高通分量；事实上，（6）中的h0滤波器是水平（或垂直）带通滤波器。由于拜耳图案CFA的矩形排列，很难在对角线方向设计类似的带通或高通滤波器。结果，低通对角滤波器将产生具有高均匀性值的平滑输出图像，使得（15）不公平地偏向对角插值。
图 10 中的“射线”图像显示了实验结果，验证了水平和垂直滤波器组插值足以处理对角线边缘。然而，当 h0=0时，除了边缘完全水平或垂直的区域外，插值射线图像会出现严重的伪影。因此，我们可以得出结论，滤波器组插值方案（6）决定了对角线边缘的插值效果。
B. Adaptive Parametrization
VI. IMPLEMENTATION AND RESULTS
A. Results
B. Computational Complexity
VII. CONCLUSION
本文提出了一种自适应同质性定向去马赛克算法。度量邻域建模技术用于比较图像中存在的颜色伪影的水平并选择插值方向。开发了滤波器组插值技术来消除混叠，并且插值伪影减少迭代抑制了颜色伪影。实验数据显示了算法的性能。