【多视几何】对极几何(Epipolar Geometry)基础及OpenCV实现:对极约束、基础矩阵、本质矩阵和单应矩阵
文章目录
- 1 对极约束(Epipolar constraint)
-
- 1.1 基本术语
- 1.2 数学推导
- 2 基础矩阵(Fundamental Matrix)
- 3 本质矩阵(Essential Matrix)
- 4 OpenCV中的相关函数
-
- 4.1 特征点检测与匹配
- 4.2 求解基础矩阵F
- 4.3 求解本质矩阵E
- 4.4 由本质矩阵E恢复相机运动
- 参考
对极几何(Epipolar Geometry)是计算机视觉理论的基础,它描述了同一场景中两幅图像(2D-2D)之间的视觉几何关系,在图像匹配、三维重建等领域应用广泛。本文中将涉及到以下知识点:
- 对极约束(Epipolar constraint)
- 基础矩阵(Fundamental Matrix)
- 本质矩阵(Essential Matrix)
单应矩阵(Homography Matrix)
1 对极约束(Epipolar constraint)
1.1 基本术语
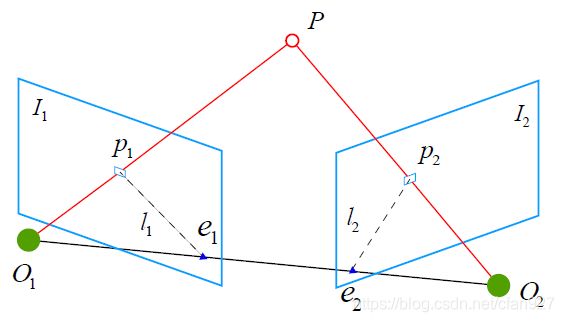
首先看一个理想情况(无噪声)。如图所示为两帧图像 I 1 , I 2 I_1,I_2 I1,I2在三维空间中的几何关系,相机光心为 O 1 , O 2 O_1,O_2 O1,O2,相机由 O 1 O_1 O1运动到 O 2 O_2 O2位置的变换为 R R R(旋转)和 t t t(平移)。 P P P为三维空间中的一个点,它在两像平面上的投影为 p 1 , p 2 p_1,p_2 p1,p2,则有以下几个术语来描述它们之间的几何关系:
- 极平面(Epipolar plane): 点 O 1 , O 2 , P O_1,O_2,P O1,O2,P三点确定的平面;
- 极点(Epipoles): O 1 O 2 O_1O_2 O1O2连线与像平面 I 1 , I 2 I_1,I_2 I1,I2的交点 e 1 , e 2 e_1,e_2 e1,e2;
- 基线(Baseline): O 1 O 2 O_1O_2 O1O2连线;
- 极线(Epipolar line): 极平面与两像平面的交线 l 1 , l 2 l_1,l_2 l1,l2。
1.2 数学推导
接下来从数学角度推导它们之间的几何关系。令 P = [ X , Y , Z ] T P=[X,Y,Z]^T P=[X,Y,Z]T,则根据针孔相机模型可以得到 P P P在两像平面上的投影点为:
{ s 1 p 1 = K P s 2 p 2 = K ( R P + t ) ⇒ { s 1 K − 1 p 1 = P s 2 K − 1 p 2 = R P + t (1) \begin{cases} s_1p_1=KP \\ s_2p_2=K(RP+t) \end{cases} \Rightarrow \begin{cases} s_1K^{-1}p_1=P \\ s_2K^{-1}p_2=RP+t \end{cases} \tag{1} {s1p1=KPs2p2=K(RP+t)⇒{s1K−1p1=Ps2K−1p2=RP+t(1)
其中 s i = 1 Z c i s_i=\frac{1}{Z_c^i} si=Zci1, 1 Z c i \frac{1}{Z_c^i} Zci1为 P P P在相机坐标空间下 Z Z Z轴坐标, K K K为相机内参矩阵, R , t R,t R,t为相机运动矩阵。
令:
{ x 1 = K − 1 p 1 x 2 = K − 1 p 2 (2) \begin{cases} x_1=K^{-1}p_1 \\ x_2=K^{-1}p_2 \tag{2} \end{cases} {x1=K−1p1x2=K−1p2(2)
则上式可变为:
{ s 1 x 1 = P s 2 x 2 = R P + t (3) \begin{cases} s_1x_1=P \\ s_2x_2=RP+t \end{cases} \tag{3} {s1x1=Ps2x2=RP+t(3)
合并这两个公式有:
s 2 x 2 = s 1 R x 1 + t (4) s_2x_2=s_1Rx_1+t \tag{4} s2x2=s1Rx1+t(4)
为了消去 t t t,对上式两侧同时与 t t t做外积(也称叉积、向量积)有:
s 2 t ∧ x 2 = s 1 t ∧ R x 1 (5) s_2t^{\wedge}x_2=s_1t^{\wedge}Rx_1 \tag{5} s2t∧x2=s1t∧Rx1(5)
考虑将上式的两项变为一项,两侧同时左乘 x 2 T x_2^T x2T:
s 2 x 2 T t ∧ x 2 = s 1 x 2 T t ∧ R x 1 (6) s_2x_2^Tt^{\wedge}x_2=s_1x_2^Tt^{\wedge}Rx_1 \tag{6} s2x2Tt∧x2=s1x2Tt∧Rx1(6)
观察等式左侧, t ∧ x 2 t^{\wedge}x_2 t∧x2是一个与 t t t和 x 2 x_2 x2都垂直的向量,若将它与 x 2 x_2 x2做内积,将得到0,于是上式可简化为:
x 2 T t ∧ R x 1 = 0 (7) x_2^Tt^{\wedge}Rx_1=0 \tag{7} x2Tt∧Rx1=0(7)
重新带入 p 1 , p 2 p_1,p_2 p1,p2(公式 ( 2 ) (2) (2))有:
p 2 T K − T t ∧ R K − 1 p 1 = 0 (8) p_2^TK^{-T}t^{\wedge}RK^{-1}p_1=0 \tag{8} p2TK−Tt∧RK−1p1=0(8)
公式 ( 7 ) (7) (7)和 ( 8 ) (8) (8)都称为对极约束,它的几何意义是 O 1 , P , O 2 O_1, P, O_2 O1,P,O2三点共面。
进一步,我们把中间部分记为两个矩阵,基础矩阵 F F F(Fundamental Matrix): F = K − T E K − 1 F=K^{-T}EK^{-1} F=K−TEK−1,本质矩阵 E E E(Essential Matrix): E = t ∧ R E=t^{\wedge}R E=t∧R,即:
x 2 T E x 1 = p 2 T F p 1 = 0 (9) x_2^TEx_1=p_2^TFp_1=0 \tag{9} x2TEx1=p2TFp1=0(9)
在SLAM中,这一步被用来估计相机位姿,即根据匹配点的像素坐标求出基础矩阵F或本质矩阵E,可通过“8点法”求解,进而求出 R , t R,t R,t,具体求解方法可参考。
2 基础矩阵(Fundamental Matrix)
基础矩阵 F F F描述了三维空间点 P P P在摄像机不同方位下成像得到的投影像素点之间的关系,即:
p 2 T F p 1 = 0 ⇒ [ u 2 v 2 1 ] T F [ u 1 v 1 1 ] = 0 (10) p_2^T F p_1=0 \\ \Rightarrow \begin{bmatrix} u_2 \\ v_2 \\ 1 \end{bmatrix}^T F \begin{bmatrix} u_1 \\ v_1 \\ 1 \end{bmatrix} =0 \tag{10} p2TFp1=0⇒⎣⎡u2v21⎦⎤TF⎣⎡u1v11⎦⎤=0(10)
3 本质矩阵(Essential Matrix)
本质矩阵 E E E实际上可以被看做是在相机归一化平面上的基本矩阵,它具有基本矩阵的所有性质。对于三维空间点 P P P,定义其在相机归一化平面上的投影坐标为:
P c = [ X c Z c Y c Z c 1 ] (11) P_c= \begin{bmatrix} \frac{X_c}{Z_c} \\ \frac{Y_c}{Z_c} \\ 1 \end{bmatrix} \tag{11} Pc=⎣⎡ZcXcZcYc1⎦⎤(11)
点 P c P_c Pc经过相机的内参矩阵后,即可投影为像素坐标,即与基础矩阵 F F F相联系(投影方程参考这篇博文中的公式(4))。则本质矩阵 E E E表示为:
[ X c 1 Z c 1 Y c 1 Z c 1 1 ] T E [ X c 2 Z c 2 Y c 2 Z c 2 1 ] = 0 (12) \begin{bmatrix} \frac{X_c^1}{Z_c^1} \\ \frac{Y_c^1}{Z_c^1} \\ 1 \end{bmatrix}^T E \begin{bmatrix} \frac{X_c^2}{Z_c^2} \\ \frac{Y_c^2}{Z_c^2} \\ 1 \end{bmatrix} =0 \tag{12} ⎣⎢⎡Zc1Xc1Zc1Yc11⎦⎥⎤TE⎣⎢⎡Zc2Xc2Zc2Yc21⎦⎥⎤=0(12)
本质矩阵 E E E可用于估计相机在两个位置的相对运动。
4 OpenCV中的相关函数
4.1 特征点检测与匹配
OpenCV里有关特征点的检测与匹配方法非常多,如SIFT、SURF、FAST、ORB、Harris等特征描述子,以及FlannBasedMatcher等特征点匹配算法,这里不再详细描述。由于初步提取的特征点匹配对会存在很多的误匹配,因此我们通常使用RANSAC等算法对得到的匹配对进行筛选,这一步骤对于后续的三维重建非常重要,错误的匹配将会严重影响重建精度。
4.2 求解基础矩阵F
在上一步得到匹配的特征点后,可以使用cv::findFundamentalMat函数来求解基础矩阵 F F F。
\\ points1, points2:std::vector<cv::Point2f>格式的匹配点对
\\ method:求解方法,包括
\\ cv::FM_7POINT - 7点法,点数N=7
\\ cv::FM_8POINT - 8点法,点数N≥8
\\ cv::FM_RANSAC - RANSAC方法,点数N≥8
\\ cv::FM_LMEDS - LMedS方法,点数N≥8
\\ ransacReprojThreshold:只对RANSAC方法有效。表示从点到极线的最大像素距离,超过该距离则点将被视为离群值,并且不被用于计算最终的基本矩阵。可将其设置为1-3
\\ confidence:用于RANSAC和LMedS方法的参数,指定了了所估计矩阵的期望置信度(概率)
CV_EXPORTS_W Mat findFundamentalMat( InputArray points1, InputArray points2,
int method = FM_RANSAC,
double ransacReprojThreshold = 3., double confidence = 0.99,
OutputArray mask = noArray() );
\\ 重载函数,用的比较少,可自行翻阅API文档
/** @overload */
CV_EXPORTS Mat findFundamentalMat( InputArray points1, InputArray points2,
OutputArray mask, int method = FM_RANSAC,
double ransacReprojThreshold = 3., double confidence = 0.99 );
4.3 求解本质矩阵E
同样的,可以利用cv::findEssentialMat来求解相机运动的本质矩阵 E E E。
\\ points1, points2:std::vector<cv::Point2f>格式的匹配点对,且点数N≥5
\\ cameraMatrix:相机内参矩阵
\\ method:提供了RANSAC和LMEDS两种算法
\\ prob:用于RANSAC和LMedS方法的参数,指定了了所估计矩阵的期望置信度(概率)。与findFundamentalMat中的参数confidence一致
\\ threshold:只对RANSAC方法有效。表示从点到极线的最大像素距离,超过该距离则点将被视为离群值,并且不被用于计算最终的基本矩阵。可将其设置为1-3。与findFundamentalMat函数中的参数ransacReprojThreshold一致
\\ mask:输出参数,维度与points1和points2一致。0表示外点outliers,1表示内点inliers
CV_EXPORTS_W Mat findEssentialMat( InputArray points1, InputArray points2,
InputArray cameraMatrix, int method = RANSAC,
double prob = 0.999, double threshold = 1.0,
OutputArray mask = noArray() );
此外,findEssentialMat也有一个重载函数,该重载函数利用给定的相机焦距和主点来计算相机的内参矩阵,实际上是一样的。
CV_EXPORTS_W Mat findEssentialMat( InputArray points1, InputArray points2,
double focal = 1.0, Point2d pp = Point2d(0, 0),
int method = RANSAC, double prob = 0.999,
double threshold = 1.0, OutputArray mask = noArray() );
4.4 由本质矩阵E恢复相机运动
利用前面得到的本质矩阵 E E E,可以使用函数cv::recoverPose来估计相机的相对运动。所使用的算法是由Nister于2003年提出的《An efficient solution to the five-point relative pose problem》,函数的参数如下:
\\ E:本质矩阵
\\ points1,points2:std::vector<cv::Point2f>格式的匹配点对。与findEssentialMat中的输入一致
\\ cameraMatrix:相机的内参矩阵
\\ R,t:算法估计的相对变换矩阵
\\ mask:标识points1和points2中的内点和外点
CV_EXPORTS_W int recoverPose( InputArray E, InputArray points1, InputArray points2,
InputArray cameraMatrix, OutputArray R, OutputArray t,
InputOutputArray mask = noArray() );
\\ 重载函数,利用焦距和主点计算内参矩阵,与上面的函数一样
CV_EXPORTS_W int recoverPose( InputArray E, InputArray points1, InputArray points2,
OutputArray R, OutputArray t,
double focal = 1.0, Point2d pp = Point2d(0, 0),
InputOutputArray mask = noArray() );
\\ E、points1、points2、cameraMatrix、R、t、mask与前面的一致
\\ distanceThresh:区分内点、外点的界限
\\ triangulatedPoints:输出,三角测量得到的特征点的三维坐标
CV_EXPORTS_W int recoverPose( InputArray E, InputArray points1, InputArray points2,
InputArray cameraMatrix, OutputArray R, OutputArray t, double distanceThresh, InputOutputArray mask = noArray(),
OutputArray triangulatedPoints = noArray());
参考
[1] 《计算机视觉中的多视图几何》
[2] 《视觉SLAM十四讲:从理论到实践》
[3] http://www.mathsword.com/slamessentialmatrixgetrt/
[4] https://blog.csdn.net/cfan927/article/details/104333527
[5] https://www.zhihu.com/question/27581884