【排序算法】详解直接插入排序和希尔排序原理及其性能分析
文章目录
- 插入排序
-
- 算法原理
- 细节分析
- 代码实现
- 复杂度分析:
- 稳定性分析:
- 与冒泡排序的对比
- 希尔排序
-
- 算法原理
- 细节分析
- 代码实现
- 复杂度分析
- 稳定性分析
- 总结对比
插入排序
算法原理
插入排序又或者说直接插入排序,是一种和冒泡排序类似的并且比较简单的排序方法,
基本思想是:把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。就像大家平时打扑克牌一样.

类似于摸牌然后将其按照顺序排列。每次摸到一张牌后,根据其点数从左到右插入到确切位置。
细节分析
用for循环控制,从最左侧的元素开始,用它右侧的元素进行依次比较(将这个右侧的元素设置为tmp),并挪动位置,最后将其插入合适的位置
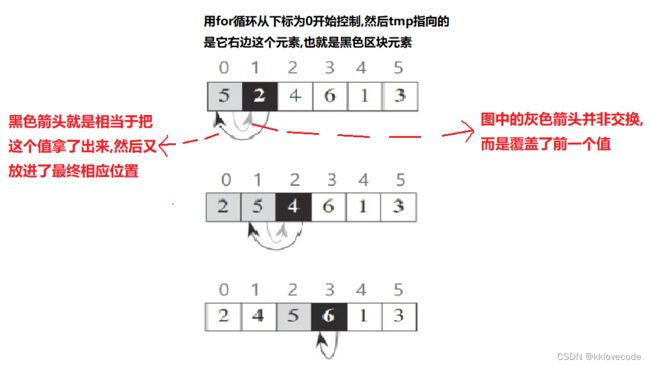
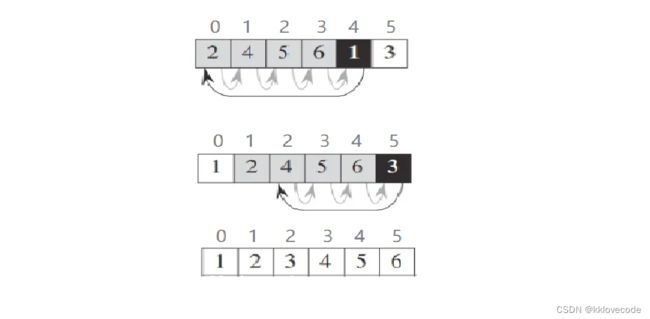
注意:看似图中是在用黑色阴影这个元素在与其前面的做交换,其实并没有,真正原理应该是把黑色阴影里面的元素拿出来(赋值给了tmp),然后与前面的进行比较,有合适的即进行覆盖,但是由于黑色阴影的值已经拿了出来(也就是tmp里面的值),所以在比较之后便可以覆盖,不会丢失这个值
代码实现
int sortArray(int* nums, int numsSize)
{
for(int i = 0;i<numsSize-1;i++)
{
int pointer = i;
int tmp = nums[i+1];
while(pointer>=0)
{
if(nums[pointer]>tmp)
{
nums[pointer+1] = nums[pointer];
pointer--;
}
else
{
break;
}
}
nums[pointer+1] = tmp;
}
}
复杂度分析:
时间复杂度
(1) 最好情况:序列已经是升序排列,在这种情况下,如果原序列本身就已经是排好了序的,那么每一趟排序只需要比较一次而不需要任何移动。此时一共需要 n-1 次比较,也就是
O(N)
(2) 最坏情况:如果原序列本身就是逆序的,那么第 i(1 ≤ i ≤ n-1)趟排序需要比较 i 次、移动 i+2 次(包括将待排序元素移动到tmp变量中和从tmp变量中移动到最终位置上)。此时,一共需要1+2+3+…+(n-1) = n(n-1)/2,所以O(N^2)
空间复杂度
直接插入排序只需要一个额外的tmp变量,所以它的空间复杂度为
O(1)
稳定性分析:
因为插入排序是只有当前元素比另外一个元素大的时候才会交换,所以相同元素的前后相对位置并不会改变,所以排序稳定
与冒泡排序的对比
若具体看冒泡排序,请看这篇文章–>冒泡排序文章戳此处
下图代表前面的元素全部有序,就最后两个无序

希尔排序
算法原理
希尔排序是希尔排序由唐纳德·希尔(Donald Shell)发明并于1959年公布,在直接插入排序算法的基础上进行改进而来的,从上面的直接插入排序我们可以看出,当原序列的长度很小时,即便它的所有元素都是无序的,此时进行的元素比较和移动的次数还是很少。所以希尔排序正是利用这点,它首先将待排序的原序列划分成很多小的序列,称为子序列。然后对这些子序列进行直接插入排序,因为每个子序列中的元素变少了,所以效率也提高了.
说简单就两点:1.先进行预排序2.直接插入排序
细节分析
具体步骤如图:
原始数组,我们设定颜色相同为一组

初始分gap组,gap = n / 2 = 5,也就是分了5组,[8,3][9,5][1,4][7,6][2,0]
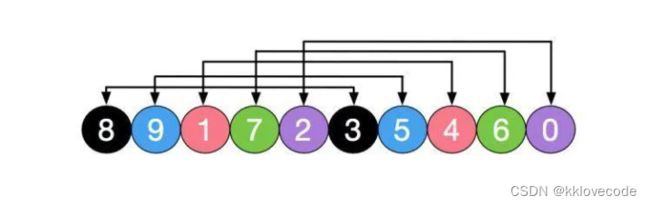
五组分别进行插入排序,此时8,9,7这种大元素被排到前面,如下图,然后再缩小gap,分为2组,[3,1,0,9,7][5,6,8,4,2]
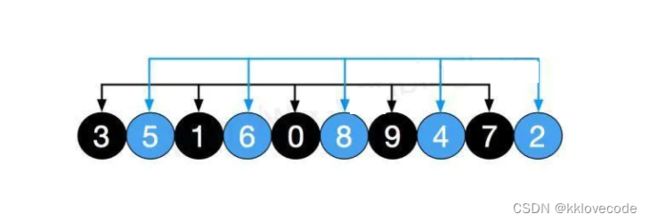
对以上两组再进行直接插入排序,结果如下,可以看出数组更加接近有序,再将gap除以2,也就是gap =1, 此时就变成了直接插入排序,此时整个数组为1组[0,2,1,4,3,5,7,6,9,8]
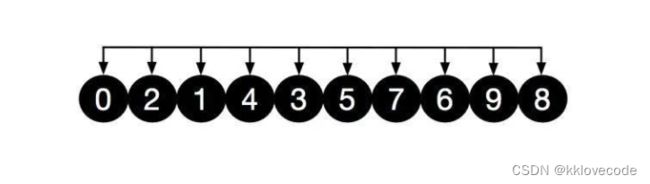
此时再进行微调,便达到了有序

由此可以看出,在前面gap不等于1时,前面几组调整都是预排序,而这种预排序完成之后就已经接近有序了,而上面在直接插入排序中我们也说到了,在顺序好的情况下,时间复杂度为O(N),而这里接近有序,时间复杂度也可以大概看作O(N),大大节省了时间,这也是希尔排序的主要作用和意义
代码实现
void sortArray(int* nums, int numsSize)
{
int gap = 6;
while(gap>1)
{
gap=gap/3+1; //上图是gap = gap/2;两者都行,但官方是更推荐gap=gap/3+1
for(int i = 0;i<numsSize-gap;i++)
{
int pointer = i;
int tmp = nums[i+gap];
while(pointer>=0)
{
if(nums[pointer]>tmp)
{
nums[pointer+gap] = nums[pointer];
pointer -= gap;
}
else
{
break;
}
}
nums[pointer+gap] = tmp;
}
}
}
通过上面你能发现希尔排序的代码无非就是在直接插入排序的基础之上多了一个while循环来控制gap分组
复杂度分析
时间复杂度
希尔排序的时间复杂度分析十分困难,希尔排序的平均时间复杂度和执行它所选择的gap分组有关,这就要设计一些复杂的数学问题,在Knuth编著的《计算机程序设计技巧》第三卷中的大量分析得出,时间复杂度大概在
O(n^(1.3)),即n的1.3次方。
空间复杂度
从我们以上的实现代码中可以看出,希尔排序只需要几个固定的额外存储空间,分别用于存储变量,这和它的待排序序列的大小无关。所以,它的空间复杂度为
O(1)。
稳定性分析
由于多次插入排序,我们知道一次插入排序是稳定的,不会改变相同元素的相对顺序,但在不同的插入排序过程中,相同的元素可能在各自的插入排序中移动,最后其稳定性就会被打乱,所以希尔排序是不稳定的。
总结对比
希尔排序和直接插入排序直接有着很强的关联性,希尔排序就是直接插入排序的加强版,利用预排序进行优化,提高排序的效率.
总的来说,直接插入排序适用于小规模或基本有序的元素,具有简单易懂的实现方法和稳定的排序性质;希尔排序适用于中大型规模的元素,通过预处理和分组插入排序的方式,提高了排序的效率。选择使用哪种算法取决于具体的需求和数据特征。

