【数据结构】二叉树详解
不知不觉断更挺久了,这篇讲二叉树
二叉树在初级数据结构中的重要性相信不需要过多解释,它既是重点也是难点。二叉树的操作基本都是用递归来实现的,中间会结合题目来展示二叉树的各种操作,所以本篇会比较长,请保持耐心看完,相信你会有收获
目录
1.树形结构
1.1树的定义
1.2树的概念
2.二叉树
2.1二叉树概念
2.2二叉树的性质
3.二叉树的操作
3.1二叉树遍历
3.1.1递归实现遍历
3.1.2非递归实现遍历
3.2获取第k层树的节点的个数
3.3求二叉树高度
3.4查找某个值是否在二叉树中
4.二叉树OJ题
4.1判断二叉树是否为完全二叉树
4.2相同的树
4.3另一棵树的子树
4.4平衡二叉树
4.5对称二叉树
4.6二叉树的最近公共祖先
4.7二叉搜索树转成双向链表
4.8依据遍历构建二叉树
4.9根据二叉树创建字符串
1.树形结构
在了解二叉树之前我们需要知道简单了解一下树的定义以及一些概念
1.1树的定义
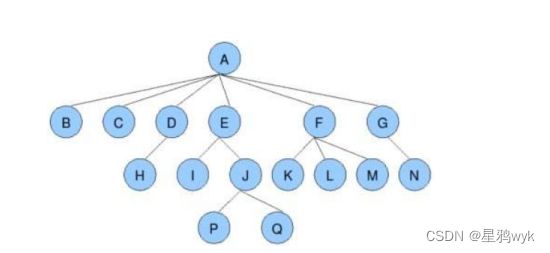
树是一种非线性的数据结构,是由多个节点组成的有层次关系的集合,看起来就像一颗倒挂的树,如下图:
树中有一个节点没有前驱节点,这个节点称为根节点
除根节点外,其余的节点又可以看成多个互不相交的集合,每一个集合就是一颗子树
1.2树的概念
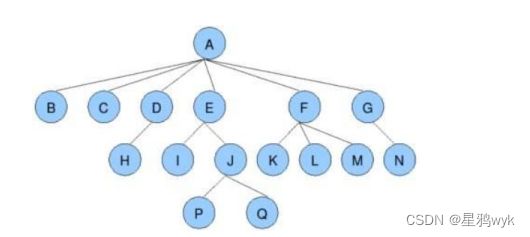
以上图作为例子来介绍一下树里面的概念
- 节点的度:一个结点含有子树的个数称为该结点的度,比如E节点的度为2
- 树的度:节点的度的最大值
- 叶子节点(终端节点):度为0的节点,比如上面的节点P、Q
- 父节点(双亲节点):一个节点的前驱节点称为此节点的父节点,如G是N的父节点
- 子节点(孩子节点):一个节点的后继节点称为此节点的子节点,如N是G的子节点
- 根节点:树中没有父节点的节点
- 节点层次:从根节点开始往下,根节点为1层,根节点的子节点为第二次,以此类推
- 树的高度:节点的最大层数
- 树的深度:不同的书中的定义不同,这里就取其中的一个定义:根节点到指定节点的最长路径的节点数,比如I,从A到I的节点数为3,所以I的深度就为3,
2.二叉树
2.1二叉树概念
有了上面的基础,我们就可以给二叉树一个定义了:
二叉树是树中的一类特殊的树,其特殊在树中所有节点的度都小于等于2,而且二叉树的子树有左右之分,而且次序不能颠倒
在二叉树中又有两个特殊的二叉树
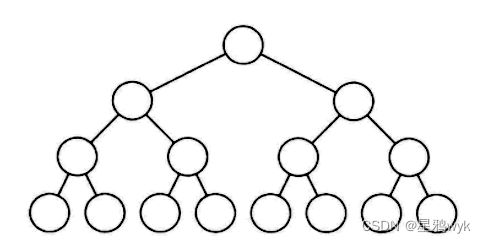
满二叉树:二叉树中每一层的节点数都达到最大值,依据等比数列求和公式计算,k层的二叉树的总的节点数量就是(2^k)-1
完全二叉树:假设二叉树有n个节点,按照从上往下,从左往右的顺序进行编号(假设从0开始编号),直至n-1的时候中间的编号不断
从图像上来说,满二叉树和完全二叉树的图如下:
2.2二叉树的性质
- 规定根节点的层数为1,那么第k层最多有2^(k-1)个节点
若规定只有根结点的二叉树的深度为1,则深度为K的二叉树的最大结点数是2^(k)-1
对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的结点个数为 n2,则有n0=n2+1
推导:n个节点共有n-1条边(一个节点对应一条边,根节点没有边)度为0、1、2的节点分别用n0、n1、n2表示,那么有 n1+2*n2+1=n0+n1+n2,化简之后就是n0=n2+1
具有n个结点的完全二叉树的深度k为 log2(n+1)向上取整
对于具有n个结点的完全二叉树,如果按照从上至下从左至右的顺序对所有节点从0开始编号,下标为i的节点
其父节点下标为(i-1)/2(向下取整)
子节点的下标为2*i+1(左孩子)2*i+2(右孩子)
3.二叉树的操作
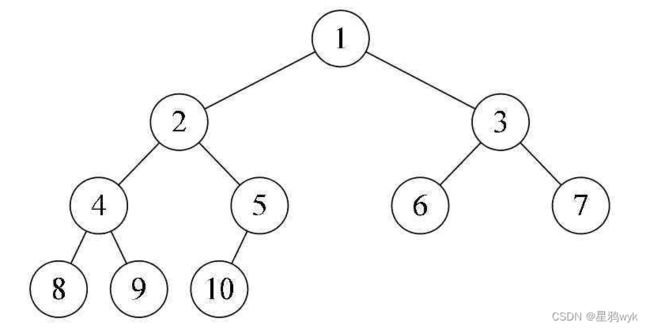
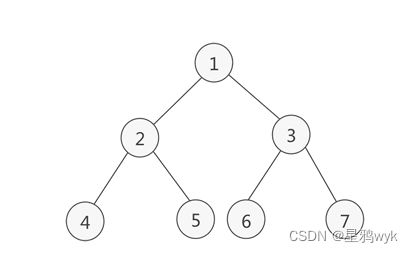
到这里就是本篇的重点了,二叉树的操作基本上都是通过递归来完成的,代码写起来可能就几行,但要理解的话却并不容易,为理解方便,我们先不构建二叉树,后面的操作以下图的二叉树为例
3.1二叉树遍历
3.1.1递归实现遍历
二叉树的遍历分前序遍历、中序遍历、后序遍历和层序遍历
所谓的前序、中序和后序指的是打印根节点的次序(根节点在最前面、中间、最后打印)
层序遍历则是从根节点开始从上往下,从左往右进行遍历
前序遍历:按照根节点->左子树->右子树的顺序进行遍历,结果为1→2→4→5→3→6→7
中序遍历:按照左子树->根节点->右子树的顺序进行遍历,结果为4→2→5→1→6→3→7
后序遍历:按照左子树->右子树->根节点的顺序进行遍历,结果为4→5→2→6→7→3→1
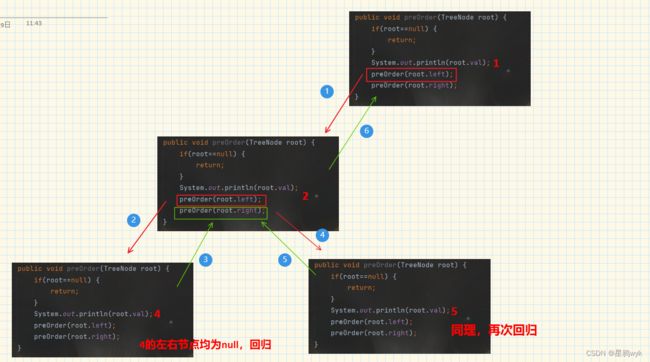
以前序遍历为例,代码如下:
public void preOrder(TreeNode root) {
if(root==null) {
return;
}
System.out.println(root.val);
preOrder(root.left);
preOrder(root.right);
}中序和后序同理,只不过代码的顺序需要变化一下
//中序遍历
public void inOrder(TreeNode root) {
if(root==null) {
return;
}
inOrder(root.left);
System.out.println(root.val);
inOrder(root.right);
}
//后序遍历
public void postOrder(TreeNode root) {
if(root==null) {
return;
}
inOrder(root.left);
inOrder(root.right);
System.out.println(root.val);
}在力扣上面有关于二叉树遍历的题目,不同的是返回值是List,题目链接:力扣
主要的代码就是上面的代码,因为返回值是List,所以建立顺序表,将遍历的值接收即可
class Solution {
public List preorderTraversal(TreeNode root) {
List ret=new ArrayList<>();
if(root==null) {
return ret;
}
ret.add(root.val);
List left=preorderTraversal(root.left);
ret.addAll(left);
List right=preorderTraversal(root.right);
ret.addAll(right);
return ret;
}
} 3.1.2非递归实现遍历
上面的遍历是通过递归完成的,下面采用非递归的方式来完成,先看前序遍历
非递归的方式需要借助栈来完成,而且根节点不能移动,所以新建一个节点cur
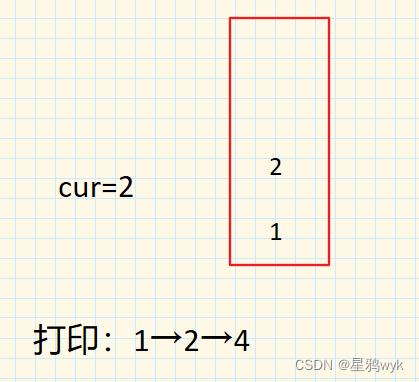
按照前序遍历的顺序,cur依次经过1、2、4,在经过这些节点的时候依次将其存放在栈中,同时依次打印
此时cur位置在4,cur来到4的左边,为空,cur=栈顶元素,再来到4的右边,为空,出栈,cur=栈顶元素,此时cur就来到2的位置
2的右边是5,将5进行打印的同时进行入栈
之后便是同样的操作,代码如下:
public void preOrder2(TreeNode root) {
if(root==null) {
return;
}
Stackstack=new Stack<>();
TreeNode cur=root;
while(cur!=null||!stack.empty()) { //cur走完二叉树时cur==null,栈中元素也为空
while(cur!=null) {
stack.push(cur);
System.out.println(cur.val);
cur=cur.left;
}
//出循环说明节点左边为空,后面来到节点右边
cur=stack.pop().right;
}
} 中序遍历的话同理,注意打印顺序
public void inOrder2(TreeNode root) {
if(root==null) {
return;
}
Stackstack=new Stack<>();
TreeNode cur=root;
while(cur!=null||!stack.empty()) {
while(cur!=null) {
stack.push(cur);
cur=cur.left;
}
cur=stack.pop();
System.out.println(cur.val);
cur=cur.right;
}
} 后序遍历因为根节点是最后打印,所以代码需要进行改变
public void postOrder2(TreeNode root) {
if(root==null) {
return;
}
Stackstack=new Stack<>();
TreeNode cur=root;
TreeNode prev=null;
while(cur!=null||!stack.empty()) {
while(cur!=null) {
stack.push(cur);
cur=cur.left;
}
TreeNode top=stack.peek();
if(top==null||top==prev) {
stack.pop();
System.out.println(top.val);
prev=top;
} else {
cur=top.right;
}
}
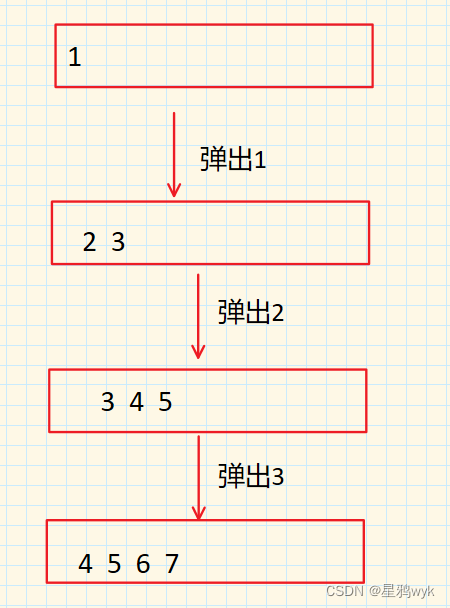
} 二叉树的层序遍历我们需要借助队列来实现
首先将根节点存入队列,然后在弹出根节点的同时存入其左右的子节点,以此类推
最后队列数字弹出的顺序就是层序遍历的顺序
代码如下:
public void levelOrder(TreeNode root) {
if(root==null) {
return;
}
Queue queue=new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()) {
TreeNode data=queue.poll();
System.out.println(data);
if(root.left!=null) {
queue.offer(root.left);
}
if(root.right!=null) {
queue.offer(root.right);
}
}
} 力扣中的层序遍历返回值是List
public List> levelOrder(TreeNode root) {
List> ret=new ArrayList<>();
if(root==null) {
return ret;
}
Queue queue=new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()) {
int size=queue.size();
List arr=new ArrayList<>();
while(size!=0) {
TreeNode cur=queue.poll();
arr.add(cur.val);
size--;
if(cur.left!=null) {
queue.offer(cur.left);
}
if(cur.right!=null) {
queue.offer(cur.right);
}
}
ret.add(arr);
}
return ret;
} 3.2获取第k层树的节点的个数
假设根节点为第1层,直接上代码:
public int getNode(TreeNode root,int k) {
if(root==null) {
return 0;
}
if(k==1) {
return 1;
}
return getNode(root.left,k-1)+getNode(root.right,k-1);
}假设我们求的是第3层的节点个数
为方便理解,我就用节点的值来代替方法里面的参数root
getNode(1,3)=getNode(2,2)+getNode(3,2)
getNode(2,2)=getNode(4,1)+getNode(5,1)=2
getNode(3,2)=getNode(6,1)+getNode(7,1)=2
3.3求二叉树高度
二叉树的高度为左右子树高度的最大值+1,左右子树的高度又等于各自左右子树的高度的最大值+1,代码如下;
public int maxDepth(TreeNode root) {
if(root==null) {
return 0;
}
int left=maxDepth(root.left);
int right=maxDepth(root.right);
return left>right? left+1: right+1;
}3.4查找某个值是否在二叉树中
如果存在,返回节点,没有则返回null
public TreeNode isIn(TreeNode root,int i) {
if(root==null) {
return null;
}
if(root.val==i) {
return root;
}
TreeNode left=isIn(root.left,i);
if(left!=null) {
return left;
}
TreeNode right=isIn(root.right,i);
if(right!=null) {
return right;
}
return null;
}4.二叉树OJ题
4.1判断二叉树是否为完全二叉树
这个需要进行层序遍历,先来看看完全二叉树和非完全二叉树之间的区别
层序遍历的时候,如果二叉树是完全二叉树,那么在出现null的时候,队列里面的元素就全部是null,非二叉树则不是,通过这一点来判断是否为完全二叉树
那么就需要循环两次,第一次碰到null的时候结束,第二次来判断队列里面剩下的元素
代码如下:
public boolean isCompleteTree(TreeNode root) {
if(root==null) {
return false;
}
Queuequeue=new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()) {
TreeNode cur=queue.poll();
if(cur!=null) {
queue.offer(cur.left);
queue.offer(cur.right);
} else {
break;
}
}
while(!queue.isEmpty()) {
TreeNode cur=queue.peek();
if(cur!=null) {
return false;
} else {
queue.poll();
}
}
return true;
} 4.2相同的树
判断是否相同我们需要判断左右子树以及根节点,我们来判断下如果两棵树不相同时有哪些情况
1:在同一位置上有一方为null,另一方不为null
2:相同位置的节点的值不同
只要出现上述情况中的一种,那么这两棵树就是不同的
代码如下:
class Solution {
public boolean isSameTree(TreeNode p, TreeNode q) {
if(q==null&&p==null) {
return true;
}
if((p==null&&q!=null)||(q==null&&p!=null)||q.val!=p.val) { //没有进入此判断说明根节点都不为null且值相等
return false;
}
boolean a=isSameTree(p.left,q.left);
boolean b=isSameTree(p.right,q.right);
return a&&b;
}
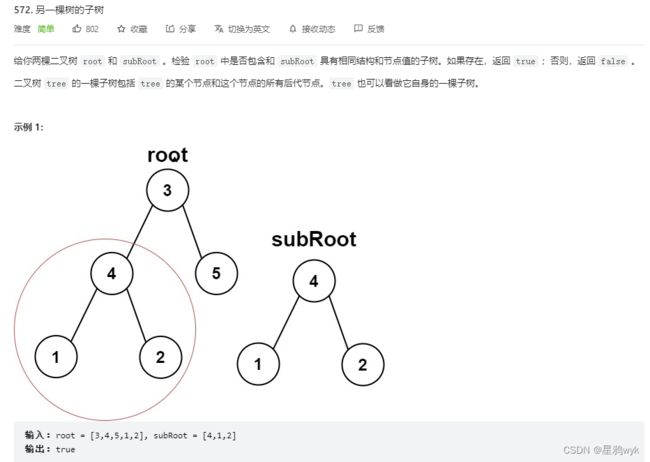
}4.3另一棵树的子树
简单来说就是判断root中是否有子树和subRoot相等,所以核心代码依旧是上一题的代码,所以这里只写增加的代码
public boolean isSubtree(TreeNode root, TreeNode subRoot) {
if(root==null) {
return false;
}
if(isSameTree(root,subRoot)){
return true;
}
if(isSubtree(root.left,subRoot)) {
return true;
}
if(isSubtree(root.right,subRoot)) {
return true;
}
return false;
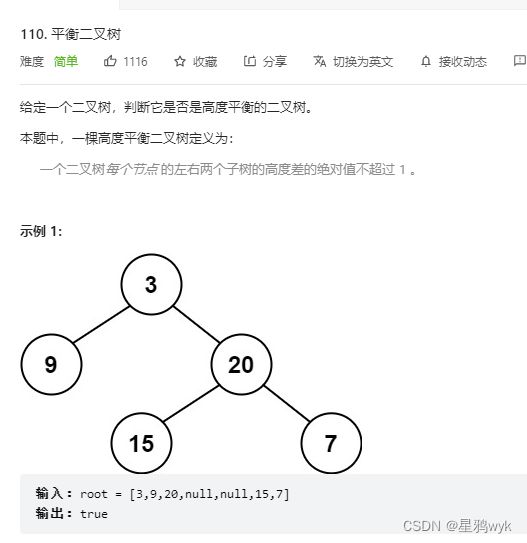
}4.4平衡二叉树
对前面的求二叉树高度的代码进行修改,在计算高度的同时求一下高度差,如果高度大于1的话就返回-1
public int maxDepth(TreeNode root) {
if(root==null) {
return 0;
}
int left=maxDepth(root.left);
int right=maxDepth(root.right);
if(left>=0 && right>=0 && Math.abs(left-right)<=1) {
return Math.max(left,right)+1;
} else {
return -1;
}
}
public boolean isBalanced(TreeNode root) {
if(root==null) {
return true;
}
int left=maxDepth(root.left);
int right=maxDepth(root.right);
return maxDepth(root)>=0;
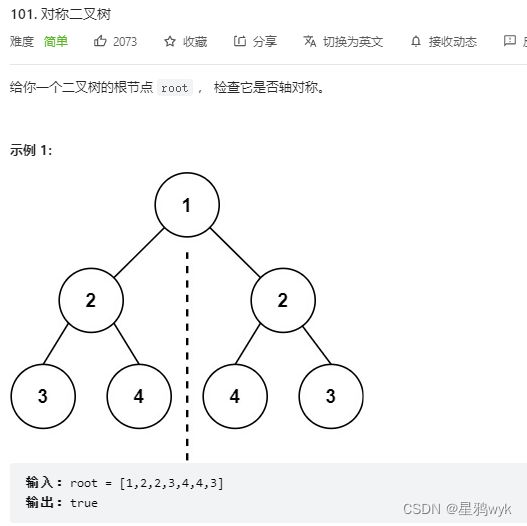
}4.5对称二叉树
二叉树不为对称二叉树的情况:左右子树的结构不对或对应位置的值不同
public boolean sym(TreeNode left,TreeNode right) {
if(left==null && right!=null) {
return false;
}
if(left!=null && right==null) {
return false;
}
if(left==null && right==null) {
return true;
}
if(left.val!=right.val) {
return false;
}
return sym(left.left,right.right)&&sym(left.right,right.left);
}
public boolean isSymmetric(TreeNode root) {
if(root==null) {
return true;
}
return sym(root.left,root.right);
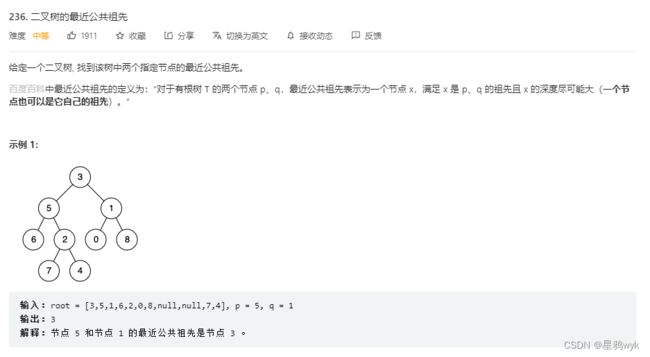
}4.6二叉树的最近公共祖先
先来分析下p和q的情况
1:p和q在异侧,二者在异侧,那么最近的公共祖先就是根节点
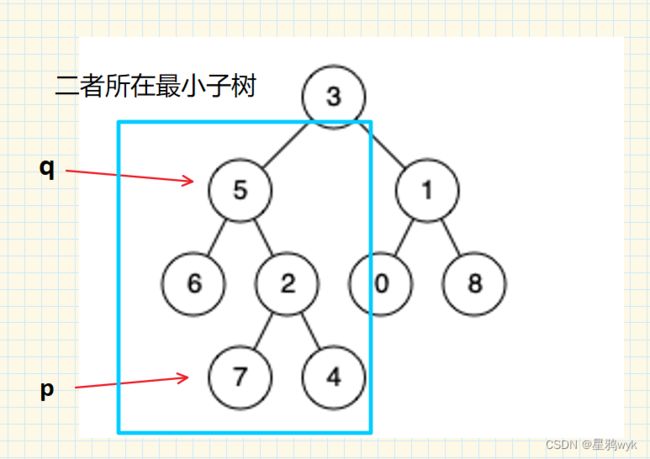
2:p和q在同侧,那就是二者所在的最小的子树的根节点(p和q有可能就是子树根节点)
代码如下:
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root==null) {
return null;
}
if(p==root||q==root) {//排除p、q之中有一个是根节点的情况,去树的两边找
return root;
}
TreeNode left=lowestCommonAncestor(root.left,p,q);
TreeNode right=lowestCommonAncestor(root.right,p,q);
if(left!=null&&right!=null) {
//left和right都不为空,p、q在树的两侧,返回根节点
return root;
} else if(left!=null&&right==null) {
//p、q均在左侧
return left;
} else if(left==null&&right!=null) {
//p、q均在右侧
return right;
}
return null;
}4.7二叉搜索树转成双向链表
题目中二叉树转成双向链表是按照中序遍历来进行转换的,如果这一点看不出来的话这题就没法写下去了
很显然节点的left充当prev,right充当next ,既然是按照中序遍历来进行转换的,那么代码也应该是在中序遍历的基础上进行修改
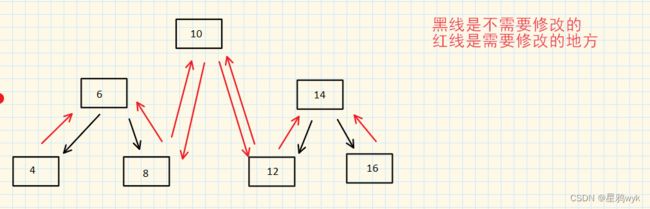
我们先来看看要改动的地方有哪些
在修改的过程中有些节点需要指向null,比如4位置,有些则不需要,所以我们不能简单的写上root.left=null之类的代码
新建节点prev,让prev=null,prev和root的初始位置如下
root.left=prev,之后二者同时向后移动,此时prev不为null,让prev.right=root,root.left=prev
后面重复此操作即可
代码如下:
TreeNode prev=null;
public void change(TreeNode root) {
if(root==null) {
return;
}
change(root.left);
root.left=prev;
if(prev!=null) {
prev.right=root;
}
prev=root;
change(root.right);
}
public TreeNode Convert(TreeNode pRootOfTree) {
if(pRootOfTree==null) {
return null;
}
change(pRootOfTree);
TreeNode head=pRootOfTree;
while(head.left!=null) {
head=head.left;
}
return head;
}4.8依据遍历构建二叉树
一般有两种形式
1.前序遍历+中序遍历或后序遍历+中序遍历
2.只有一种遍历,但里面写明了null的位置
先来说说第一种情况如何来构建二叉树,假设二叉树前序遍历是[3,9,20,15,7],中序遍历是[9,3,15,20,7]
前序遍历第一个数是3,所以3就是根节点,再根据3在中序遍历中的位置得到9位于3的左子树,15、20和7是3的右子树
前序遍历第二个数是9,所以9是左子树的根节点,根据9在中序遍历中的位置,左子树构建完成
左子树构建完成,所以前序遍历第三个数20就是右子树的根节点,依据其在中序遍历中的位置,15在作,7在右
具体的图如下
后序遍历+中序遍历也是同样的过程,后序遍历最后一个是根节点,倒数第二个是右子树根节点
构建二叉树依据的就是上述的推导过程
还是来看例题
我们要做的就是在preorder中找根节点,然后在inorder中确定左右子树,重复此步骤
public int index=0;
public TreeNode setTree(int[] preorder, int[] inorder,int left,int right) {
if(left>right) {
return null;
}
TreeNode root=new TreeNode(preorder[index]);
//找根节点在中序遍历数组中的位置
int rootIndex=findIndex(inorder,left,right,preorder[index]);
++index;
//创建左右子树
root.left=setTree(preorder,inorder,left,rootIndex-1);
root.right=setTree(preorder,inorder,rootIndex+1,right);
return root;
}
public int findIndex(int[] inorder,int left,int right,int val) { //在指定位置之间找子树的根节点的下标
for(int i=left;i<=right;++i) {
if(inorder[i]==val) {
return i;
}
}
return -1;
}
public TreeNode buildTree(int[] preorder, int[] inorder) {
return setTree(preorder,inorder,0,inorder.length-1);
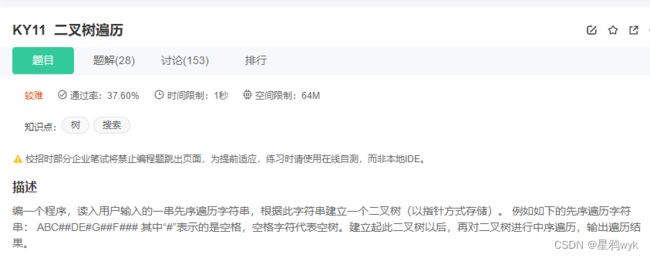
}再来看下第二种情况
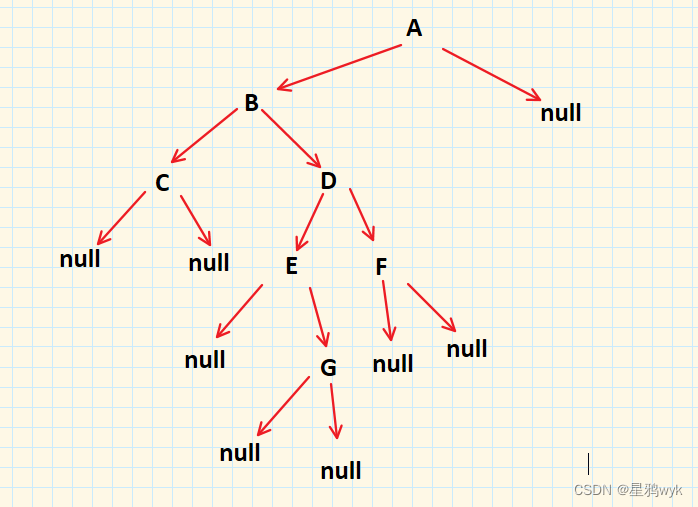
因为已经将null表明,所以我们可以将这个二叉树画出来
因为题目中说的是前序遍历,所以将前序遍历的代码修改,这里只写构建二叉树的代码,后面的中序遍历省略
public static int i = 0;
public static TreeNode binaryTree(String str) {//根据字符串创建二叉树
//创建二叉树需要遍历字符串,以递归的形式遍历,所以i要定义在外面
TreeNode root=null;
if(str.charAt(i)!='#') {
//不为井号的话就实例化节点
root=new TreeNode(str.charAt(i));
i++;
root.left=binaryTree(str);
root.right=binaryTree(str);
} else {
i++;
}
return root;
}4.9根据二叉树创建字符串
先说说字符串的意思:括号外的为根节点,括号里面表示这个根节点的子树的情况,近的是左子树,远的是右子树
实现的具体操作
- 左子树不为空加上“(”,递归左子树,左子树走完加上“)”,右子树同理
- 右子树为空,左子树不为空的情况以及左右都为空,什么都不要做
- 左子树为空,右子树不为空的情况需要+(),因为右子树是离的较远的那个
StringBuilder arr=new StringBuilder();
public String tree2str(TreeNode root) {
if(root==null) {
return null;
}
arr.append(root.val);
if(root.left!=null) { //递归左子树
arr.append("(");
tree2str(root.left);
arr.append(")");
} else {
if(root.right!=null) {
arr.append("()");
}
}
if(root.right!=null) { //递归右子树
arr.append("(");
tree2str(root.right);
arr.append(")");
}
return arr.toString();
}到这不知不觉都一万多字了,还是第一次写这么长的博客,之前断更了挺久,之后会保持更新频率
二叉树完