·读书笔记」 具体数学
头脑一热,然后买了《具体数学》,差点还买了英文版
后来觉得自己英文太烂,还是决定购买的中文版
书是前几天到的,从2014.8.1号开始看,坚持每天看一点,学习一点.
为了监督自己,决定在这里开一贴,记录我的学习路程。
时间:2014.8.1 地点:家里
今天阅读的是本书的第一章,讲的是递归问题,也是算法的基础,当然这里主要讲的是数学。但是没办法,我是一名ACMer,必须要和程序紧密联系在一起。
我觉得明天还需要花一天时间来看这章,需要解决下后面的习题以及再加深点体会。
第一章 递归问题
1.1 汉诺塔
1.2 平面上的直线
1.3 约瑟夫问题
这里我重点看的是约瑟夫问题,,我想这个问题不用我多说了,基本上学过点数学或者是学过的算法的都知道.
最原始的Josephus传说,是计算到最后存活的两个人(Josephus 和 他的朋友)
而我们现在考虑的约瑟夫环问题,一般是考虑最后存活下来的人。
约瑟夫问题首先给定N,N代表人数,然后给定K,代表每轮K个人,将其杀死。
当然还有扩展,给定N,然后指定一个人开始计算,每个人有自己独立的Ki
讨论一: N给定,K=2 J(n)代表N = n 时,最后幸存的人的编号
这是书上讨论的,具体的话可以最终推出一个公式 J(2^m + l) = 2*l + 1
所以解决这类问题可以达到O(1)的复杂度
讨论二: N给定,K给定
解决这个问题(包括解决讨论一),都可以用模拟的方法,既可以用数组来模拟,也可以用循环链表来模拟但是时间复杂度为O(N*K)
这里学习到了另外一个O(N)的数学解法。就是反向逆推。

具体数学上介绍并且推导了 k = 2 时候的约瑟夫环问题 当然还有当人数为K = M时的情况。 这里我们得到递推公式 假设 k = 3,N = 9,W = 0 第一个被杀的坑定是3(也就是k) W = 3 N 1 2 3 4 5 6 7 8 9 N 4 5 6 7 8 9 1 2 V S S X S S S S S S V S S X S S S S S N 7 8 9 1 2 4 5 N 1 2 4 5 7 8 V S S X S S S S V S S X S S S N 5 7 8 1 2 N 1 2 5 7 V S S X S S V S S X S N 7 1 2 N 7 1 V S S X V X S N 1 V S 再来考虑一般的情况 N 1 2 3 4 5 6 7 8 9 N 4 5 6 7 8 9 1 2 V S S X S S S S S S V S S X S S S S S 第一次数值4的下标W1 = 3 (W从0开始) 第二次数值4的下标W2 = 0 W1 = ( W2 + 3 ) % 9 = (0 + 3) % 9 = 3 也就是W1 = ( W2 + k ) % N 第三次数值4的下标W3 = 5 W2 = ( W3 + 3) % 8 = (5 + 3) % 8 = 0 也就是W2 = ( W3 + k ) % (N-1) 这就是一般情况,相邻的两个相同数的下标关系 最后一次,只剩下没有被杀的幸存者,下标必然是0 那么这里就可以考虑往前推了(从后往前推) 核心算法: int ans=0; //存活人最后的序号W为0 for(i=2;i<=n;i++) ans = (ans+k)%i; 因为题目是下标为1开始,所以最后答案 + 1 即可
理论联系实际,我做了几道和约瑟夫环有关系的题目,具体可以参看 暑期刷题
POJ 1781 - In Danger ( K = 2 )
HDU 2925 - Musical Chair ( 给定其他k )
UVA 133 - the Dole Queue ( 双向模拟 )
先总结到这里,以后有做题目或者新的体会一定会继续补充。
对于平面上的直线问题,高中的时候大家肯定学过。就是问N条直线最多能把平面分成几块区域

这里想谈谈本章需要重点体会的证明方法--数学归纳法 ( 我只是想强调数学归纳法很重要 ) 对的,就是我们高中学习的数学归纳法,非常有用 对于一个定理或者公式的证明,一般有反证法和数学归纳法 今天第一天看着本书,果断绝地数学归纳法确实NB强大V587 这里我直接引用Wiki: 最简单和常见的数学归纳法是证明当n等于任意一个自然数时某命题成立。 证明分下面两步: 骨牌一个接一个倒下,就如同一个值到下一个值的过程。 证明当n = 1时命题成立。 证明如果在n = m时命题成立,那么可以推导出在n = m+1时命题也成立。(m代表任意自然数) 这种方法的原理在于:首先证明在某个起点值时命题成立,然后证明从一个值到下一个值的过程有效。当这两点都已经证明,那么任意值都可以通过反复使用这个方法推导出来。把这个方法想成多米诺效应也许更容易理解一些。例如:你有一列很长的直立着的多米诺骨牌,如果你可以: 证明第一张骨牌会倒。 证明只要任意一张骨牌倒了,那么与其相邻的下一张骨牌也会倒。 那么便可以下结论:所有的骨牌都会倒下

这点我也想强调很重要 找规律的题目或者是需要证明公式的题目,甚至说任何题目 都需要先从小的情形开始。 比如平面上的直线,就应该从0,1,2这样的小数字开始考虑并推断
----------------------------------------------------------------------------------
时间:2014.8.2-2014.8.3 地点:家里
继续补充第一章留下的其他问题。现在来研究汉诺塔问题
最普通的汉诺塔问题,来自印度的一个典故,这里就不多说了。
总之,规则就是有三个柱子A,B,C,开始的时候A柱上有若干盘子,盘子只允许大的在下小的在上。
问将所有盘子移动到C柱的最小步数是多少。
A.普通汉诺塔(三柱)
想先来模拟一下 步骤 ( 假设有n个盘子 ) :
1. 将 n-1 个盘子 从 A 借助 C 移动到 B (n-1 步)
2. 将第 n 号盘子 从 A 移动到 C (1 步)
3. 将 n-1 个盘子 从 B 借助 A移动到 C (n-1 步)
那么可以得到一个递推关系了
F(n) = 2*F(n-1) + 1
两边 +1, 得:
F(n)+1 = 2( F(n-1) + 1 )
令S(n) = F(n) + 1, 有:
S(n) = 2S(n-1),又S(1) = 1+1 = 2
可得 S(n) = 2^n
最终证得:
F(n) = 2^n - 1
结合步骤:可以编写一个递归程序来进一步了解基础的汉诺塔,我在别人的blog找到一个很不错的ppt

#include<stdio.h> void move(int n,char a,char b,char c) { if(n==1) printf("\t%c->%c\n",a,c); //当n只有1个的时候直接从a移动到c else { move(n-1,a,c,b); //第n-1个要从a通过c移动到b printf("\t%c->%c\n",a,c);//再将n从a移动到c move(n-1,b,a,c); //n-1个移动过来之后b变开始盘,b通过a移动到c,这里要主义三根柱子的顺序要有所交换,因为这个时候n-1个盘子已经被移动到了b柱,所以应该是借助a柱,移动到c柱 } } int main() { int n; printf("请输入要移动的块数:"); scanf("%d",&n); move(n,'a','b','c'); }
接下来是一系列的汉诺塔问题 (such as 四柱汉诺塔,有约束条件的汉诺塔,中间状态求解,步数求解等等)
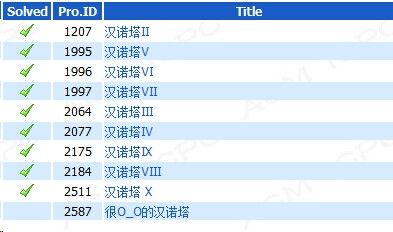
B.多柱汉诺塔最优解问题
关于汉诺塔四柱问题的研究,可以参看这个论文《多柱汉诺塔最优算法设计探究》
修为尚浅就不自己班门弄斧了,不过一开始对于四柱问题,想法也是先将n-2个盘子从A移动到D,
然后将n-1移动到B,n移动到C,n-1再移动到C,再将n-2个盘子移动到C。
推出的递推公式为: F(n) = F(n-2)*2 + 3
随便再多想想,很容易感觉这个递推是错误的(不是最优的)
而正确的递推式 : F(n) = min(F(n-r) + 2^r - 1) [1 <= r <= n]
从四柱汉诺塔你可以得到启示,对于更多柱的情况,算法的复杂度更难估计。
求解N柱汉诺塔,需要用到N-1柱汉诺塔的公式。
四柱,需要用到三柱的公式 也就是2^n -1
五柱,要用到四柱,而四柱又要用到三柱。。。
C.汉诺塔Ⅲ
在汉诺塔原来的基础上增加约束条件: 1.A,B,C 三个柱子,A不能直接移动到C,必须经过中间的辅助柱子
这里还是用递推来推出公式 1. 将n-1 块盘子 从A柱借助B柱移动到C柱 F(n-1) 2. 将n从A移动到B 1
3. 将n-1 块盘子 从C柱借助B柱移动到A柱 F(n-1)
4. 将n从B移动到C 1
5. 将n-1 块盘子 从A柱借助B柱移动到C柱 F(n-1)
那么,可以推出递推式:
F(n) = F(n-1)* 3 + 2
封闭公式是:
F(n) = 3^n - 1
D.汉诺塔Ⅳ
在汉诺塔原来的基础上增加约束条件: 1.A,B,C 三个柱子,A不能直接移动到C,必须经过中间的辅助柱子
2.最大的盘子可以放在最上面(且只允许最大的盘子有这个规则)
1. 将n-2 块盘子 从A柱借助B柱移动到C柱 F(n-2) 2. 将n-1从A移动到B 1
3. 将n 从A移动到B 1
4. 将n-2 块盘子 从C柱借助B柱移动到A柱 F(n-2)
5. 将n 从B移动到C 1
6. 将n-1从B移动到C 1
4. 将n-2 块盘子 从A柱借助B柱移动到C柱 F(n-2)
递推公式:
T(n) = F(n-2)*3 + 4 [ 前面求得 F(n) = 3^n - 1 ]
封闭公式:
T(n) = (3^(n-2)-1)*3 + 4 = 3^(n-1) + 1
递推公式:
T(n-1) = 3^(n-2) + 1
T(n) - T(n-1) = 3^(n-1) - 3^(n-2) = 2*(3^(n-2))
T(n) = T(n-1) + 2*(3^(n-2))
T(n) = T(n-1) + 2*(3^(n-2)+1) - 2
T(n) = T(n-1) + 2T(n-1) - 2
T(n) = 3*T(n-1) - 2
