1143.最长公共子序列,1035.不相交的线,53. 最大子序和
1143. 最长公共子序列
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
- 例如,
"ace"是"abcde"的子序列,但"aec"不是"abcde"的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
示例 1:
输入:text1 = "abcde", text2 = "ace" 输出:3 解释:最长公共子序列是 "ace" ,它的长度为 3 。
示例 2:
输入:text1 = "abc", text2 = "abc" 输出:3 解释:最长公共子序列是 "abc" ,它的长度为 3 。
示例 3:
输入:text1 = "abc", text2 = "def" 输出:0 解释:两个字符串没有公共子序列,返回 0 。
提示:
1 <= text1.length, text2.length <= 1000text1和text2仅由小写英文字符组成。
子序列问题中最经典的LCS问题,公式都记熟了:
伪代码和图解如下:
Java代码:
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
int[][] dp = new int[text1.length() + 1][text2.length() + 1];
for (int i = 1; i <= text1.length(); i++) {
char char1 = text1.charAt(i - 1);
for (int j = 1; j <= text2.length(); j++) {
char char2 = text2.charAt(j - 1);
if (char1 == char2) {
dp[i][j] = dp[i - 1][j - 1] + 1;
}
else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[text1.length()][text2.length()];
}
}1035. 不相交的线
在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。
现在,可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线,这些直线需要同时满足满足:
-
nums1[i] == nums2[j] - 且绘制的直线不与任何其他连线(非水平线)相交。
请注意,连线即使在端点也不能相交:每个数字只能属于一条连线。
以这种方法绘制线条,并返回可以绘制的最大连线数。
示例 1:
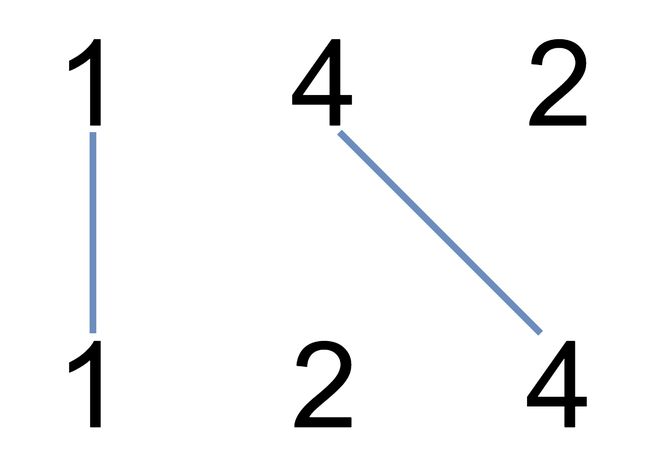
输入:nums1 = [1,4,2], nums2 = [1,2,4] 输出:2 解释:可以画出两条不交叉的线,如上图所示。 但无法画出第三条不相交的直线,因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。
示例 2:
输入:nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2] 输出:3
示例 3:
输入:nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1] 输出:2
提示:
1 <= nums1.length, nums2.length <= 5001 <= nums1[i], nums2[j] <= 2000
我们重新回顾一下LCS问题:
然后你就会发现和这题简直一毛一样,无非就是把上题的字符串换成数组而已:
class Solution {
public int maxUncrossedLines(int[] nums1, int[] nums2) {
int len1 = nums1.length;
int len2 = nums2.length;
int[][] dp = new int[len1 + 1][len2 + 1];
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (nums1[i - 1] == nums2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[len1][len2];
}
}53. 最大子数组和
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4] 输出:6 解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1] 输出:1
示例 3:
输入:nums = [5,4,-1,7,8] 输出:23
提示:
1 <= nums.length <= 105-104 <= nums[i] <= 104
进阶:如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的 分治法 求解。
这题之前用贪心做过,思路是计数累加,累加和小于 0 就重新开始计数,每次计数都求计数过程中和的最大值,再从这些局部最优解中找出全局最优解。dp的思路为记录包含当前元素的最大连续子序列之和,dp[i] 的值要么是 dp[i - 1] 加上当前元素,要么从头开始计算当前连续子序列和,值直接刷新为当前元素的值。
class Solution {
public int maxSubArray(int[] nums) {
if (nums.length == 1) return nums[0];
int res = nums[0];
int dp[] = new int[nums.length];
dp[0] = nums[0];
for (int i = 1; i < nums.length; i++) {
dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
res = res > dp[i] ? res : dp[i];
}
return res;
}
}然后我们发现 dp[i] 总是由 dp[i - 1] 和 nums[i] 得来,可以直接压缩。
class Solution {
public int maxSubArray(int[] nums) {
if (nums.length == 1) return nums[0];
int res = nums[0];
int pre = nums[0];
for (int i = 1; i < nums.length; i++) {
pre = Math.max(pre + nums[i], nums[i]);
res = res > pre ? res : pre;
}
return res;
}
}