输入格式:
n
v1,v2,...,vn
m
输出格式:
若有解,则输出全部找零方案,每输出一种
若无解,则输出“None”
输入样例1:
6
3 1 4 3 2 7
9
输出样例1:
3 1 3 2
3 4 2
4 3 2
2 7
输入样例2:
5
5 3 4 6 7
2
输出样例2:
None
AC代码:
#include
using namespace std;
void dfs(vector> &res, vector &nums, vector &v, int m, int index) {
if (m <= 0) {
if (m == 0)
res.push_back(v);
return;
}
for (int i = index; i < nums.size(); i++) {
v.push_back(nums[i]);
dfs(res, nums, v, m - nums[i], i + 1);
v.pop_back();
}
}
int main()
{
int i, j, n, m;
cin >> n;
vector>res;
vectornums(n, 0), v;
for (i = 0; i < n; i++) {
cin >> nums[i];
}
cin >> m;
dfs(res, nums, v, m, 0);
if (res.empty())
cout << "None" << endl;
else {
for (i = 0; i < res.size(); i++) {
for (j = 0; j < res[i].size(); j++) {
if (j == 0)
cout << res[i][j];
else
cout << " " << res[i][j];
}
cout << endl;
}
}
system("pause");
return 0;
}
7-4 整数拆分(回溯法)
将一个正整数n拆分成若干个正整数的和(至少两个数,n<=100)。
输入格式:
一个正整数n
输出格式:
若干行,每行一个等式(数与数之间要求非降序排列)。最后一行给出解的总个数
输入样例:
在这里给出一组输入。例如:
4
输出样例:
4=1+1+1+1
4=1+1+2
4=1+3
4=2+2
4
AC代码:
#include
using namespace std;
void dfs(vector> &res, vector &v, int n, int count, int index) {
if (count >= n) {
if (count == n && v.size() > 1)
res.push_back(v);
return;
}
for (int i = index; i <= n; i++) {
v.push_back(i);
dfs(res, v, n, count + i, i);
v.pop_back();
}
}
int main()
{
int i, j, k, n;
cin >> n;
vector>res;
vectorv;
dfs(res, v, n, 0, 1);
for (i = 0; i < res.size(); i++) {
cout << n << "=";
for (j = 0; j < res[i].size(); j++) {
if (j == 0)
cout << res[i][j];
else
cout << "+" << res[i][j];
}
cout << endl;
}
cout << res.size() << endl;
system("pause");
return 0;
}
7-5 数字三角形问题(动态规划)
给定一个由n行数字组成的数字三角形如下图所示。试设计一个算法,计算出从三角形的顶至底的一条路径,使该路径经过的数字总和最大。
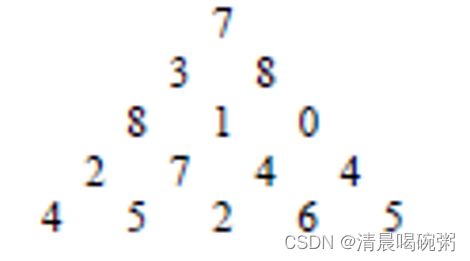
对于给定的由n行数字组成的数字三角形,计算从三角形的顶至底的路径经过的数字和的最大值。
输入格式:
输入数据的第1行是数字三角形的行数n,1≤n≤100。接下来n行是数字三角形各行中的数字。所有数字在0..99之间。
输出格式:
输出数据只有一个整数,表示计算出的最大值。
输入样例:
在这里给出一组输入。例如:
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
输出样例:
在这里给出相应的输出。例如:
30
AC代码:
#include
using namespace std;
int main()
{
int i, j, k, n;
cin >> n;
vector>nums(n), dp(n);
for (i = 0; i < n; i++) {
nums[i].resize(i + 1);
dp[i].resize(i + 1);
}
for (i = 0; i < n; i++) {
for (j = 0; j < nums[i].size(); j++) {
cin >> nums[i][j];
}
}
for (i = nums.size() - 1, j = 0; j < nums[i].size(); j++) {
dp[i][j] = nums[i][j];
}
for (i = nums.size() - 2; i >= 0; i--) {
for(j = 0; j < nums[i].size(); j++) {
dp[i][j] = max(dp[i + 1][j], dp[i + 1][j + 1]) + nums[i][j];
}
}
cout << dp[0][0] << endl;
system("pause");
return 0;
}
7-6 幂集(回溯法)
有一个含n个数的数组a,所有元素均不相同,设计一个算法求其所有子集(幂集)。
例如:1 2 3的幂集{}、{3}、{2}、{2,3}、{1}、{1,3}、{1,2}、{1,2,3}
输入格式:
第一行输入元素个数n,再依次输入n个数。
输出格式:
输出子集数
输入样例:
3
1 2 3
输出样例:
8
AC代码:
#include
using namespace std;
void backtracking(vector &nums, int index, int &count) {
count++;
for (int i = index; i < nums.size(); i++) {
backtracking(nums, i + 1, count);
}
}
int main()
{
int i, j, k, n, count = 0;
cin >> n;
vectornums(n, 0);
for (i = 0; i < n; i++) {
cin >> nums[i];
}
backtracking(nums, 0, count);
cout << count << endl;
system("pause");
return 0;
}
7-7 子集和问题(回溯/深度优先搜索)
给定n个不同的正整数集合w=(w1,w2,…,wn)和一个正数W,要求找出w的子集s,使该子集中所有元素的和为W。
输入格式:
第一行输入n和W,第二行依次输入n个数。
输出格式:
每行输出一个符合要求的子集。
输入样例:
4 31
11 13 24 7
输出样例:
11 13 7
24 7
AC代码:
#include
using namespace std;
void dfs(vector> &res, vector &v, vector &nums, int n, int index) {
if (n <= 0) {
if (n == 0)
res.push_back(v);
return;
}
for (int i = index; i < nums.size(); i++) {
v.push_back(nums[i]);
dfs(res, v, nums, n - nums[i], i + 1);
v.pop_back();
}
}
int main()
{
int i, j, k, n, m;
cin >> m >> n;
vectornums(m, 0), v;
vector>res;
for (i = 0; i < m; i++) {
cin >> nums[i];
}
dfs(res, v, nums, n, 0);
for (i = 0; i < res.size(); i++) {
for (j = 0; j < res[i].size(); j++) {
cout << res[i][j] << " ";
}
cout << endl;
}
system("pause");
return 0;
}
7-8 工作分配问题(回溯/深度优先搜索)
设有n件工作分配给n个人。将工作i分配给第j个人所需的费用为cij 。 设计一个算法,对于给定的工作费用,为每一个人都分配1 件不同的工作,并使总费用达到最小。
输入格式:
输入数据的第一行有1 个正整数n (1≤n≤20)。接下来的n行,每行n个数,表示工作费用。
输出格式:
将计算出的最小总费用输出到屏幕。
输入样例:
3
10 2 3
2 3 4
3 4 5
输出样例:
9
AC代码:
#include
using namespace std;
void dfs(vector> &nums, vector &v, vector &temp, int count, int &res, int index) {
if (count > res)
return;
if (v.size() == nums.size()) {
res = min(res, count);
return;
}
for (int i = index; i < nums.size(); i++) {
for (int j = 0; j < nums[i].size(); j++) {
if (temp[j]) {
v.push_back(nums[i][j]);
temp[j] = false;
dfs(nums, v, temp, count + nums[i][j], res, i + 1);
v.pop_back();
temp[j] = true;
}
}
}
}
int main()
{
int i, j, k, n, count = 0, res = INT_MAX;
cin >> n;
vector>nums(n, vector(n, 0));
vectortemp(n, true);
vectorv;
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
cin >> nums[i][j];
}
}
dfs(nums, v, temp, count, res, 0);
cout << res << endl;
system("pause");
return 0;
}
7-9 岛屿数量(深度优先搜索)
给你一个由 1(陆地)和 0(水)组成的n*m的二维网格,请你计算网格中岛屿的数量num。
岛屿总是被水包围,并且每座岛屿只能由水平方向或竖直方向上相邻的陆地连接形成。例如
此为两个岛屿
此外,你可以假设该网格的四条边均被水包围。1<=n,m<=100
输入格式:
第一行中给出网格长宽n,m
接下来的n行表示网格情况
输出格式:
岛屿个数num
输入样例:
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1
输出样例:
3
AC代码:
#include
using namespace std;
vector>item = {{0, 1}, {0, -1}, {-1, 0}, {1, 0}};
void dfs(vector> &nums, vector> &temp, int x, int y) {
int new_x, new_y;
for (auto & dir : item) {
new_x = x + dir.first;
new_y = y + dir.second;
if (new_x >= 0 && new_x < nums.size() && new_y >= 0 && new_y < nums[0].size()) {
if (temp[new_x][new_y] && nums[new_x][new_y]) {
temp[new_x][new_y] = false;
dfs(nums, temp, new_x, new_y);
}
}
}
}
int main()
{
int i, j, n, m, res = 0;
cin >> m >> n;
vector>nums(m, vector(n, 0));
vector>temp(m, vector(n, true));
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) {
cin >> nums[i][j];
}
}
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) {
if (temp[i][j] && nums[i][j]) {
dfs(nums, temp, i, j);
res++;
}
}
}
cout << res << endl;
system("pause");
return 0;
}
7-10 小H喜欢睡觉(广度优先搜索)
小H十分喜欢睡觉,这天他起来一看,居然9.30了,而他答应了10点要到小W家去,小H想走知道小H到小W家的最短时间是多少,你能帮帮他吗。
地图是n * m的网格,每个单元是一个开放空间或建筑物(无法通过),小H的加在(1,1),小W 在(x,y)处,他只能上下左右移动,每一步需要1分钟。 输入数据可确保小W家可到达。
输入格式:
第一行具有两个正整数n,m,以空格(1 <= n,m <= 100)隔开,n为行,m为列
接下来是两个正整数x,y,用空格隔开(1 <= x <= n,1 <= y <= m)指示教学大楼的坐标
接下来是n行和m列的地图,0表示开放空间,1表示障碍物。
输出格式:
对于每个测试用例,输出一行包含整数的行,该行给出了小H到达小W家所需的最短时间(以分钟为单位)。
输入样例:
5 4
4 3
0 0 1 0
0 0 0 0
0 0 1 0
0 1 0 0
0 0 0 1
输出样例:
7
AC代码:
#include
using namespace std;
vector>dirs = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
typedef struct point {
int x, y, step;
}point;
int bfs(vector> &nums, vector> &visit, int x, int y, int p, int q) {
point start;
start.x = x;
start.y = y;
start.step = 0;
queueQ;
Q.push(start);
while (!Q.empty()) {
if (Q.front().x == p && Q.front().y == q) {
return Q.front().step;
}
int new_x, new_y;
for (auto & dir : dirs) {
new_x = Q.front().x + dir.first;
new_y = Q.front().y + dir.second;
if (new_x >= 0 && new_x < nums.size() && new_y >= 0 && new_y < nums[0].size()) {
if (nums[new_x][new_y] == 0 && visit[new_x][new_y] == false) {
point temp;
temp.x = new_x;
temp.y = new_y;
temp.step = Q.front().step + 1;
Q.push(temp);
visit[new_x][new_y] = true;
}
}
}
Q.pop();
}
return -1;
}
int main()
{
int i, j, k, n, m, res;
int p, q;
cin >> m >> n >> p >> q;
vector>nums(m, vector(n, 0));
vector>visit(m, vector(n, false));
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) {
cin >> nums[i][j];
}
}
visit[0][0] = true;
res = bfs(nums, visit, 0, 0, p - 1, q - 1);
cout << res << endl;
system("pause");
return 0;
}
7-11 迷宫问题(深度优先搜索)
小明置身于一个迷宫,请你帮小明找出从起点到终点的最短路程。
小明只能向上下左右四个方向移动。
输入格式:
第一行是两个整数n和m (1≤ m, n ≤100),表示迷宫的长和宽。接下来是n行,每行m个数字,表示整个迷宫。空地格子用0表示,障碍物用1表示,小明所在起点用3表示,终点用4表示。
输出格式:
如果能够到达终点,输出一个整数,表示小明从起点到目的地所需的最短时间。如果不能到达终点,输出“unreachable”。
输入样例1:
5 5
1 0 1 1 1
1 0 4 1 0
1 0 0 1 0
0 0 0 1 0
1 0 3 0 1
输出样例1:
3
输入样例2:
5 5
3 0 1 1 1
1 0 1 1 0
1 0 1 1 0
0 0 0 1 0
1 0 1 0 4
输出样例2:
unreachable
AC代码:
#include
using namespace std;
vector>dirs = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
int res = INT_MAX;
void dfs(vector> &nums, vector> &visit, int x, int y, int p, int q, int step) {
if (x == p && y == q) {
res = min(res, step);
return;
}
int new_x, new_y;
for (auto & dir : dirs) {
new_x = x + dir.first;
new_y = y + dir.second;
if (new_x >= 0 && new_x < nums.size() && new_y >= 0 && new_y < nums[0].size()) {
if ((nums[new_x][new_y] == 4 || nums[new_x][new_y] == 0) && visit[new_x][new_y] == false) {
visit[new_x][new_y] = true;
dfs(nums, visit, new_x, new_y, p, q, step + 1);
visit[new_x][new_y] = false;
}
}
}
}
int main()
{
int i, j, k, n, m, start_x, start_y, p, q;
cin >> m >> n;
vector>nums(m, vector(n, 0));
vector>visit(m, vector(n, false));
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) {
cin >> nums[i][j];
if (nums[i][j] == 3) {
start_x = i;
start_y = j;
}
if (nums[i][j] == 4) {
p = i;
q = j;
}
}
}
visit[start_x][start_y] = true;
dfs(nums, visit, start_x, start_y, p, q, 0);
if (res == INT_MAX)
cout << "unreachable" << endl;
else
cout << res << endl;
system("pause");
return 0;
}
7-12 走迷宫Ⅱ(广度优先搜索+优先队列)
一个迷宫由n行m列格子组成。有的格子是空地,可以走;有的格子处是障碍物,不能走;此外,有的格子处是一扇关闭的门,需要打开门后才能通过。小明准备从迷宫的某一格子(起点)走到另一个格子(终点),假定他只可以朝上、下、左、右四个方向移动,不能斜着走。每移动一个位置(格子)需要1分钟,打开一扇门需要额外的1分钟。给定迷宫和小明的起点和终点,请编写程序计算小明从起点到终点最短需要花费多少时间。
输入格式:
输入包含多组数据,每组数据第一行是两个整数n和m (1≤m,n≤100),表示迷宫的长和宽。接下来是n行,每行m个数字,表示整个迷宫。空地格子用0表示,障碍物用1表示,门用2表示,小明所在起点用3表示,终点用4表示。
输出格式:
对于每组数据,如果能够到达终点,输出一个整数,表示小明从起点到目的地所需的最短时间。如果不能到达终点,输出“unreachable”。
输入样例:
5 5
1 0 1 1 1
1 0 4 1 0
1 0 0 1 2
0 0 2 1 0
1 0 3 0 1
5 5
3 0 1 1 1
1 0 1 1 0
1 0 1 1 2
0 0 2 1 0
1 0 1 0 4
输出样例:
4
unreachable
AC代码:
#include
using namespace std;
vector>dirs ={{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
typedef struct point {
int x, y, step;
}point;
struct cmp {
bool operator() (point a, point b) {
return a.step > b.step;
}
};
string bfs(vector> &nums, vector> &visit, int start_x, int start_y, int p, int q) {
point start;
start.x = start_x;
start.y = start_y;
start.step = 0;
priority_queue, cmp>Q;
Q.push(start);
while (!Q.empty()) {
int x = Q.top().x;
int y = Q.top().y;
int step = Q.top().step;
if (x == p && y == q) {
return to_string(step);
}
int new_x, new_y;
for (auto & dir : dirs) {
new_x = x + dir.first;
new_y = y + dir.second;
if (new_x >= 0 && new_x < nums.size() && new_y >= 0 && new_y < nums[0].size()) {
if ((nums[new_x][new_y] == 2 || nums[new_x][new_y] == 4 || nums[new_x][new_y] == 0) && visit[new_x][new_y] == false) {
point temp;
temp.x = new_x;
temp.y = new_y;
if (nums[new_x][new_y] == 2)
temp.step = step + 2;
else
temp.step = step + 1;
visit[new_x][new_y] = true;
Q.push(temp);
}
}
}
Q.pop();
}
return "unreachable";
}
int main()
{
int i, j, n, m;
vectorres;
while (scanf("%d %d", &m, &n) != EOF && true) {
int start_x, start_y, p, q;
vector>nums(m, vector(n, 0));
vector>visit(m, vector(n, false));
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) {
cin >> nums[i][j];
if (nums[i][j] == 3) {
start_x = i;
start_y = j;
}
if (nums[i][j] == 4) {
p = i;
q = j;
}
}
}
visit[start_x][start_y] = true;
res.push_back(bfs(nums, visit, start_x, start_y, p, q));
}
for (i = 0; i < res.size(); i++) {
cout << res[i] << endl;
}
system("pause");
return 0;
}
7-14 h0252.拯救行动(广度优先搜索)
公主被恶人抓走,被关押在牢房的某个地方。牢房用N*M (N, M <= 200)的矩阵来表示。矩阵中的每项可以代表道路(@)、墙壁(#)、和守卫(x)。
英勇的骑士(r)决定孤身一人去拯救公主(a)。我们假设拯救成功的表示是“骑士到达了公主所在的位置”。由于在通往公主所在位置的道路中可能遇到守卫,骑士一旦遇到守卫,必须杀死守卫才能继续前进。
现假设骑士可以向上、下、左、右四个方向移动,每移动一个位置需要1个单位时间,杀死一个守卫需要花费额外的1个单位时间。同时假设骑士足够强壮,有能力杀死所有的守卫。
给定牢房矩阵,公主、骑士和守卫在矩阵中的位置,请你计算拯救行动成功需要花费最短时间。
输入格式:
第一行为一个整数S,表示输入的数据的组数(多组输入)
随后有S组数据,每组数据按如下格式输入
1、两个整数代表N和M, (N, M <= 200).
2、随后N行,每行有M个字符。"@"代表道路,"a"代表公主,"r"代表骑士,"x"代表守卫, "#"代表墙壁。
输出格式:
如果拯救行动成功,输出一个整数,表示行动的最短时间。
如果不可能成功,输出"Impossible"
输入样例:
2
7 8
#@#####@
#@a#@@r@
#@@#x@@@
@@#@@#@#
#@@@##@@
@#@@@@@@
@@@@@@@@
13 40
@x@@##x@#x@x#xxxx##@#x@x@@#x#@#x#@@x@#@x
xx###x@x#@@##xx@@@#@x@@#x@xxx@@#x@#x@@x@
#@x#@x#x#@@##@@x#@xx#xxx@@x##@@@#@x@@x@x
@##x@@@x#xx#@@#xxxx#@@x@x@#@x@@@x@#@#x@#
@#xxxxx##@@x##x@xxx@@#x@x####@@@x#x##@#@
#xxx#@#x##xxxx@@#xx@@@x@xxx#@#xxx@x#####
#x@xxxx#@x@@@@##@x#xx#xxx@#xx#@#####x#@x
xx##@#@x##x##x#@x#@a#xx@##@#@##xx@#@@x@x
x#x#@x@#x#@##@xrx@x#xxxx@##x##xx#@#x@xx@
#x@@#@###x##x@x#@@#@@x@x@@xx@@@@##@@x@@x
x#xx@x###@xxx#@#x#@@###@#@##@x#@x@#@@#@@
#@#x@x#x#x###@x@@xxx####x@x##@x####xx#@x
#x#@x#x######@@#x@#xxxx#xx@@@#xx#x#####@
输出样例:
13
7
AC代码:
#include
using namespace std;
vector>dirs = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
typedef struct point {
int x, y, step;
}point;
struct cmp {
bool operator() (point a, point b) {
return a.step > b.step;
}
};
int bfs(vector &G, vector> &visit, int start_x, int start_y, int p, int q) {
point start;
start.x = start_x;
start.y = start_y;
start.step = 0;
priority_queue, cmp>Q;
Q.push(start);
while (!Q.empty()) {
int x = Q.top().x;
int y = Q.top().y;
int step = Q.top().step;
if (x == p && y == q)
return step;
int new_x, new_y;
for (auto & dir : dirs) {
new_x = x + dir.first;
new_y = y + dir.second;
if (new_x >= 0 && new_x < G.size() && new_y >= 0 && new_y < G[0].length()) {
if ((G[new_x][new_y] == '@' || G[new_x][new_y] == 'a' || G[new_x][new_y] == 'x') && visit[new_x][new_y] == false) {
point temp;
temp.x = new_x;
temp.y = new_y;
if (G[new_x][new_y] == 'x')
temp.step = step + 2;
else
temp.step = step + 1;
visit[new_x][new_y] = true;
Q.push(temp);
}
}
}
Q.pop();
}
return -1;
}
string solve() {
int i, j, m, n, start_x, start_y, p, q, res;
cin >> m >> n;
vectorG(m);
vector>visit(m, vector(n, false));
for (i = 0; i < m; i++) {
cin >> G[i];
int index1, index2;
index1 = G[i].find("r");
index2 = G[i].find("a");
if (index1 != -1) {
start_x = i;
start_y = index1;
}
if (index2 != -1) {
p = i;
q = index2;
}
}
visit[start_x][start_y] = true;
res = bfs(G, visit, start_x, start_y, p, q);
if (res == -1)
return "Impossible";
return to_string(res);
}
int main()
{
int i, j, k, n, t;
cin >> t;
vectorres;
while (t--) {
res.push_back(solve());
}
for (i = 0; i < res.size(); i++) {
cout << res[i] << endl;
}
system("pause");
return 0;
}
