《数据结构、算法与应用 —— C++语言描述》学习笔记 — 二叉树
《数据结构、算法与应用 —— C++语言描述》学习笔记 — 二叉树
- 一、树
- 二、二叉树
- 1、二叉树的定义
- 2、二叉树的特性
- 三、二叉树数组描述
- 四、二叉树接口
- 五、链表实现
-
- 1、节点类
- 2、接口
- 3、拷贝构造函数
- 4、遍历方式
-
- (1)节点/元素处理函数实现
- (2)前序遍历
- (3)中序遍历
- (4)后序遍历
- (5)层次遍历
- 5、构造树
- 6、高度
- 7、使用
一、树
一棵树 t 是一个非空的有限元素的集合,其中一个元素为根,其余的元素组成 t 的子树。如图:
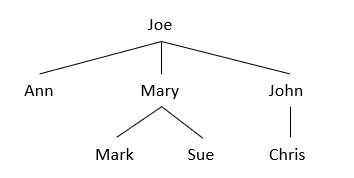
每个元素代表一个节点。树根画在上面,其子树画在下面,在根与子树的根之间有一条边。同样的,每一颗子树也是根在其上,其子树在下。在一棵树中,一个元素节点及其孩子节点之间用边连接。例如在上图中,ANN、Mary、John 是 Joe 的孩子,Joe 是他们的父母。有相同父母的孩子为兄弟。在图中,ANN、Mary、John 是兄弟,而 Mark 和 Chris 不是兄弟。此外还有其它术语:孙子、祖父、祖先、后代等等。在树中没有孩子的元素称为叶子。
树的另一常用术语为级。树根是1级,其孩子是2级,孩子的孩子是3级等等。一棵树的高度或深度是树中级的个数。在上图中,树的高度是3。一个元素的度是指起孩子的个数。叶节点的度为0。一棵树的度是其元素的度的最大值。
二、二叉树
1、二叉树的定义
一棵二叉树 t 是有限个元素的集合。当二叉树非空是,其中有一个元素称为根,余下的元素被划分成两棵二叉树,分别称为 t 的左子树和右子树。
二叉树和树的根本区别在于:
二叉树的每个元素都恰好有两棵子树(其中一个或两个可能为空)。而树的每个元素可有任意数量的子树。
在二叉树中,每个元素的子树都是有序的,也就是说,有左子树和右子树之分。而树的子树可以是无序的。
2、二叉树的特性
特性1 一棵二叉树有 n 个元素, n > 0 n \gt 0 n>0,它有 n - 1 条边。
特性2 一棵二叉树的高度为 h, h ≥ 0 h \ge 0 h≥0,它最少有 h 个元素,最多有 2 h − 1 2^h - 1 2h−1 个元素。
特性3 一棵二叉树有 n 个元素, n > 0 n \gt 0 n>0,它的高度最大为 n,最小高度为 ⌈ l o g 2 ( n + 1 ) ⌉ \lceil log_2(n+1) \rceil ⌈log2(n+1)⌉。
当高度为 h 的二叉树恰好有 2 h − 1 2^h - 1 2h−1 个元素时,称其为满二叉树。如图:
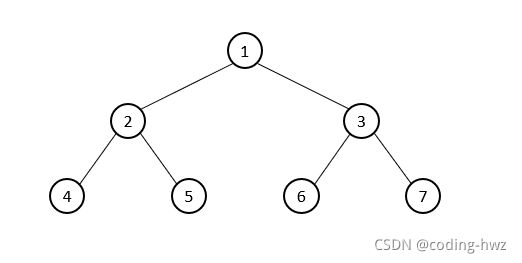
对高度为 h 的满二叉树的元素,从第一层到最后一层,在每一次中从左至右,顺序编号,从 1 到 2 h − 1 2^h - 1 2h−1。假设从满二叉树中删除 k 个编号为 2 h − i 2^h - i 2h−i 元素, 1 ≤ i ≤ k < 2 h 1 \le i \le k \lt 2^h 1≤i≤k<2h,所得到的二叉树为完全二叉树。满二叉树是完全二叉树的一个特例。有 n 个元素的完全二叉树,其高度为 ⌈ l o g 2 ( n + 1 ) ⌉ \lceil log_2(n+1) \rceil ⌈log2(n+1)⌉。
特性4 假设完全二叉树的一元素其编号为 i, 1 ≤ i ≤ n 1 \le i \le n 1≤i≤n。有以下关系成立:
(1)如果 i = 1 i=1 i=1,则该元素为二叉树的根。若 i > 1 i \gt 1 i>1,则其父结点的编号为 ⌊ i 2 ⌋ \lfloor \frac{i}{2} \rfloor ⌊2i⌋。
(2)如果 2 i > n 2i \gt n 2i>n,则该元素无做孩子。否则,其左孩子的编号为 2 i 2i 2i。
(3)如果 2 i + 1 > n 2i + 1 \gt n 2i+1>n,则该元素无右孩子。否则,其右孩子的编号为 2 i + 1 2i+1 2i+1。
三、二叉树数组描述
二叉树的数组表示利用了特性4,把二叉树看做是缺少了部分元素的完全二叉树,如图所示(虚线为缺少部分):
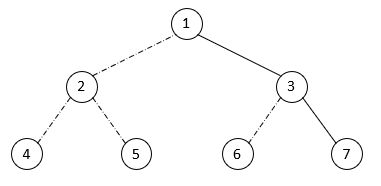
在数组表示中,二叉树的元素按照其编号存储在数组的相应位置。上图所对应的数组表示为:
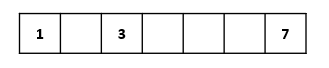
可以看出,当缺少的元素很多时,这种表示方法非常浪费空间。一个有 n 个元素的二叉树可能最多需要 2 n 2^n 2n 个空间来存储。当根节点以外的每个节点都是其父节点的右孩子时,存储空间浪费的最多。只有当缺少的元素数目比较少时,这种描述方法才是有用的
四、二叉树接口
#pragma once
#include visitFunc 为用户提供的在遍历过程中处理每个节点的函数符。
五、链表实现
1、节点类
#pragma once
template<typename T>
class binaryTreeNode
{
public:
T element;
binaryTreeNode* leftChild;
binaryTreeNode* rightChild;
binaryTreeNode(const T& element, binaryTreeNode* leftChild = nullptr, binaryTreeNode* rightChild = nullptr):
element(element)
{
this->leftChild = leftChild;
this->rightChild = rightChild;
}
};
2、接口
#pragma once
#include "binaryTree.h"
#include "binaryTreeNode.h"
#include 3、拷贝构造函数
这里只列出析构和内部拷贝接口:
template<typename T>
inline linkedBinaryTree<T>::~linkedBinaryTree()
{
visitNodeFunc = [](binaryTreeNode<T>* node) {delete node; };
postOrder(root);
visitNodeFunc = std::function<void(binaryTreeNode<T>*)>();
}
template<typename T>
inline void linkedBinaryTree<T>::makeCopyAndSwap(const linkedBinaryTree& other)
{
auto copyHashTable = makeCopy(other);
swap(copyHashTable);
}
template<typename T>
inline linkedBinaryTree<T> linkedBinaryTree<T>::makeCopy(const linkedBinaryTree& other)
{
linkedBinaryTree returnBinaryTree;
returnBinaryTree.root = new binaryTreeNode<T>(other.root->element);
returnBinaryTree.treeSize = other.treeSize;
copyChildNodes(other.root, returnBinaryTree.root);
return returnBinaryTree;
}
template<typename T>
inline void linkedBinaryTree<T>::copyChildNodes(binaryTreeNode<T>* src, binaryTreeNode<T>* dst)
{
if (src->leftChild != nullptr)
{
dst->leftChild = new binaryTreeNode<T>(src->leftChild->element);
copyChildNodes(src->leftChild, dst->leftChild);
}
if (src->rightChild != nullptr)
{
dst->rightChild = new binaryTreeNode<T>(src->rightChild->element);
copyChildNodes(src->rightChild, dst->rightChild);
}
}
template<typename T>
inline void linkedBinaryTree<T>::swap(linkedBinaryTree& other)
{
using std::swap;
swap(this->root, other.root);
swap(this->treeSize, other.treeSize);
}
copyChildNodes 也是一种前序遍历,只是当前节点的元素发生在上一级调用时。只有构建了父节点才能构造其左右子树。
4、遍历方式
有四种遍历二叉树的常用方式:前序遍历、中序遍历、后序遍历、层次遍历。
(1)节点/元素处理函数实现
书中的接口很神奇,它的遍历接口参数为 (void(*)(binaryTree
template<typename T>
inline void linkedBinaryTree<T>::dealNodeVisit(binaryTreeNode<T>* node)
{
if (visitNodeFunc)
{
visitNodeFunc(node);
}
else if (visitFunc)
{
visitFunc(node->element);
}
}
(2)前序遍历
前序遍历的思想是:对任何一个输入节点,
①访问当前元素;
②如果有左孩子,则处理左孩子;
③如果有右孩子,则处理右孩子。
这里的处理指的是递归调用前序遍历函数。
template<typename T>
inline void linkedBinaryTree<T>::preOrder(std::function<void(T)> visitFunc)
{
this->visitFunc.swap(visitFunc);
preOrder(root);
}
template<typename T>
inline void linkedBinaryTree<T>::preOrder(binaryTreeNode<T>* node)
{
if (node == nullptr)
{
return;
}
dealNodeVisit(node);
preOrder(node->leftChild);
preOrder(node->rightChild);
}
(3)中序遍历
中序遍历的思想是:对任何一个输入节点,
①如果有左孩子,则处理左孩子;
②访问当前元素;
③如果有右孩子,则处理右孩子。
template<typename T>
inline void linkedBinaryTree<T>::inOrder(std::function<void(T)> visitFunc)
{
this->visitFunc.swap(visitFunc);
inOrder(root);
}
template<typename T>
inline void linkedBinaryTree<T>::inOrder(binaryTreeNode<T>* node)
{
if (node == nullptr)
{
return;
}
inOrder(node->leftChild);
dealNodeVisit(node);
inOrder(node->rightChild);
}
(4)后序遍历
后序遍历的思想是:对任何一个输入节点,
①如果有左孩子,则处理左孩子;
②如果有右孩子,则处理右孩子。
③访问当前元素;
template<typename T>
inline void linkedBinaryTree<T>::postOrder(std::function<void(T)> visitFunc)
{
this->visitFunc.swap(visitFunc);
postOrder(root);
}
template<typename T>
inline void linkedBinaryTree<T>::postOrder(binaryTreeNode<T>* node)
{
if (node == nullptr)
{
return;
}
postOrder(node->leftChild);
postOrder(node->rightChild);
dealNodeVisit(node);
}
这是为什么我们选择借助后序遍历实现空间释放。每次都是先释放左右子树,再释放自身,可以保证所有节点得到释放。
(5)层次遍历
层次遍历的思想是:从顶层到底层,从左到右,依次访问树的元素。不难看出,我们需要借助队列保存所有节点。为什么是队列呢?因为处理完首节点,要将其孩子节点加入到容器的末尾以保证处理顺序。
template<typename T>
inline void linkedBinaryTree<T>::levelOrder(std::function<void(T)> visitFunc)
{
this->visitFunc.swap(visitFunc);
levelOrder(root);
}
template<typename T>
inline void linkedBinaryTree<T>::levelOrder(binaryTreeNode<T>* node)
{
std::deque<binaryTreeNode<T>*> queueNodesInSameLevel;
while (node != nullptr)
{
dealNodeVisit(node);
if (node->leftChild != nullptr)
{
queueNodesInSameLevel.push_back(node->leftChild);
}
if (node->rightChild != nullptr)
{
queueNodesInSameLevel.push_back(node->rightChild);
}
if (queueNodesInSameLevel.empty())
{
break;
}
node = queueNodesInSameLevel.front();
queueNodesInSameLevel.pop_front();
}
}
5、构造树
树是通过根元素和左右子树构造而得:
template<typename T>
inline void linkedBinaryTree<T>::makeTree(const T& element, linkedBinaryTree<T>& left, linkedBinaryTree<T>& right)
{
root = new binaryTreeNode<T>(element, left.root, right.root);
treeSize = left.treeSize + right.treeSize + 1;
// deny access from trees left and right
left.root = right.root = nullptr;
left.treeSize = right.treeSize = 0;
}
为了简便,我们这里没有使用右值引用,但其实现确实为移动语义。
6、高度
template<typename T>
inline int linkedBinaryTree<T>::height()
{
return height(root);
}
template<typename T>
inline int linkedBinaryTree<T>::height(binaryTreeNode<T>* node)
{
if (node == nullptr)
{
return 0;
}
int leftChildHeight = height(node->leftChild);
int rightChildHeight = height(node->rightChild);
return std::max(leftChildHeight, rightChildHeight) + 1;
}
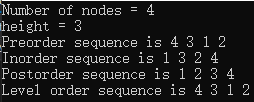
7、使用
简单改了改书后的源码:
// test linked binary tree class
#include