步进电机直线插补

1.插补运动简介

1.1 概念

需要一种方法能把已知点中间所有微小直线段的坐标点全都计算出来，从而形成符合精度要求的刀具运动轨迹，这种计算方法就叫插补（interpolation），也称为“数据点的密化”。

插补算法法所要解决的就是根据加工速度的要求，在给定的数据点坐标之间，连续计算出若干中间点的坐标值。而这些中间点的坐标值以一定的精度逼近理论的轨迹。由于计算每个中间点所消耗的时间直接影响数控系统的控制速度，坐标值的计算精度又影响数控系统的控制精度，所以插补算法是整个数控系统的控制核心。

1.2 常见插补方法

插补应该是一类计算方法，而不只是某一种。目前，根据不同的条件给出的插补方法实现有很多种，在这里我们简单的介绍几种常用的插补方法。根据输出信号的方式不同，插补算法大致可以分为脉冲增量插补和数字增量插补两大类。

数字增量插补算法基本上都用在以伺服电机为驱动装置的闭环数控系统。

脉冲增量插补算法适合以步进电机为驱动装置的开环数控系统。

1.2.1 脉冲增量插补

脉冲增量插补。这类插补算法的特点是每次插补运算只产生一个行程增量，用一个个脉冲的方式输出到电机以驱动机床刀具或工作台运动。每发出一个脉冲，刀具或工作台向 X 或 Y 轴方向移动一个脉冲当量。通常只需加法、乘法和移位即可完成插补。这类算法一般适合中等精度和中等速度的数控系统中，插补误差不超过一个脉冲当量，不过输出脉冲的速率主要受插补计算的时间限制。

脉冲增量插补在计算过程中不断向 X、Y 各个坐标轴发出进给脉冲，以驱动坐标轴所在的步进电机运动。目前已经有很多属于脉冲增量插补算法的具体算法被用到实际的生产应用中。

如 逐点比较法、数字积分法、Bresenham 算法。

（1）逐点比较法。逐点比较法最开始被称为区域判别法，又称代数运算法或醉步式近似法。是一种逐点计算、判别偏差并修正逼近理论轨迹的方法。逐点比较法的基本思想就是在刀具按理论轨迹运动加工工件轮廓的时候，不断比较刀具与工件轮廓之间的相对位置，并根据比较结果决定下一步的进给方向，使刀具向减小误差的方向移动。

（2）数字积分法。数字积分法又称数字微分分析法 DDA(Digital Differential Analyzer)，简称积分器。这种算法是在数字积分器的基础上建立起来的一种插补算法，可以较为方便的实现一次、二次曲线的插补。具有运算速度快、脉冲分配均匀、易于实现多坐标联动及描绘平面各种函数曲线的特点，应用比较广泛。
在普通的开环数控系统中，逐点比较法和数字积分法应用最为广泛，其中逐点比较法计算简单直观容易理解，并且输出为步进式的脉冲信号，尤其适合步进电机驱动的开环数控系统。

2.逐点比较法直线插补

一句话概括；逐点比较法是以阶梯折现来逼近直线段和圆弧等曲线。
每完成一次进给都需要以下 4 个步骤：

• 偏差判别：判断当前加工点和理论加工图形之间的相对位置，决定下一步 X、Y 轴的运动方向；

• 坐标进给：根据得到的偏差，控制指定坐标轴进给（移动）一步，逼近理论图形，减小误差；

• 偏差计算：计算新的加工点与理论加工图像间的偏差大小，作为下一步判别的依据；

• 终点判别：判断是否到达加工终点，如果到达终点则停止插补，如过没有到达终点，则回到第一个步骤，不断重复整个过程，直到到达轨迹终点。

逐点比较法可以插补直线和圆弧，并且都存在上述 4 个步骤，这里讲解逐点比较法如何实现直线插补。

2.1 偏差判别

2.2 坐标进给

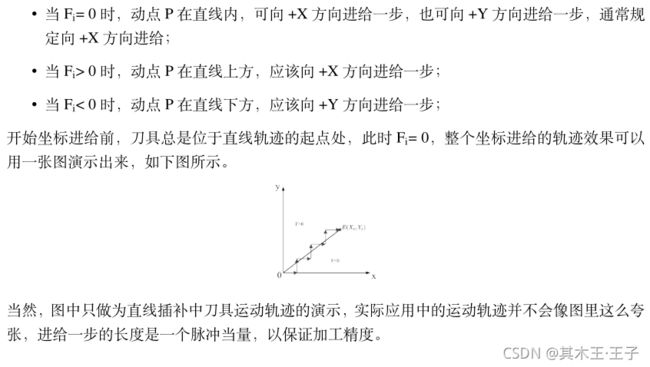
逐点比较法的坐标进给有两个原则：一是减小加工动点相对于理论轨迹的位置偏差，二是进给方向总是平行与某个坐标轴。根据这个原则以及上个步骤偏差判别的信息，可以得出直线插补的坐标进给方法：

2.3 偏差计算

概括总结就是

2.4 终点判别

2.5 参考程序

终点判别采用 总步长法

/**
  * @brief  直线增量插补运动
  * @param  inc_x：终点坐标X的增量
  * @param  inc_y：终点坐标Y的增量
  * @param  speed：进给速度
  * @retval 无
  */
void InterPolation_Move(uint32_t inc_x, uint32_t inc_y, uint16_t speed)
{
  /* 偏差清零 */
  interpolation_para.deviation = 0;
  
  /* 设置终点坐标 */
  interpolation_para.endpoint_x = inc_x;
  interpolation_para.endpoint_y = inc_y;
  /* 所需脉冲数为X、Y坐标增量之和 */
  interpolation_para.endpoint_pulse = inc_x + inc_y;
  
  /* 第一步进给的活动轴为X轴 */
  interpolation_para.active_axis = x_axis;
  /* 计算偏差 */
  interpolation_para.deviation -= interpolation_para.endpoint_y;
  
  /* 设置速度 */
  __HAL_TIM_SET_COMPARE(&TIM_StepperHandle, step_motor[x_axis].pul_channel, speed);
  __HAL_TIM_SET_COMPARE(&TIM_StepperHandle, step_motor[y_axis].pul_channel, speed);
  __HAL_TIM_SET_AUTORELOAD(&TIM_StepperHandle, speed * 2);
  
  /* 使能主输出 */
  __HAL_TIM_MOE_ENABLE(&TIM_StepperHandle);
  /* 开启X轴比较通道输出 */
  TIM_CCxChannelCmd(MOTOR_PUL_TIM, step_motor[interpolation_para.active_axis].pul_channel, TIM_CCx_ENABLE);
  HAL_TIM_Base_Start_IT(&TIM_StepperHandle);
}

/**
  * @brief  定时器比较中断回调函数
  * @param  htim：定时器句柄指针
  *	@note   无
  * @retval 无
  */
void HAL_TIM_PeriodElapsedCallback(TIM_HandleTypeDef *htim)
{
  uint32_t last_axis = 0;
  
  /* 记录上一步的进给活动轴 */
  last_axis = interpolation_para.active_axis;
  
  /* 根据上一步的偏差，判断的进给方向，并计算下一步的偏差 */
  if(interpolation_para.deviation >= 0)
  {
    /* 偏差>0，在直线上方，进给X轴，计算偏差 */
    interpolation_para.active_axis = x_axis;
    interpolation_para.deviation -= interpolation_para.endpoint_y;
  }
  else
  {
    /* 偏差<0，在直线下方，进给Y轴，计算偏差 */
    interpolation_para.active_axis = y_axis;
    interpolation_para.deviation += interpolation_para.endpoint_x;
  }
  
  /* 下一步的活动轴与上一步的不一致时，需要换轴 */
  if(last_axis != interpolation_para.active_axis)
  {
    TIM_CCxChannelCmd(htim->Instance, step_motor[last_axis].pul_channel, TIM_CCx_DISABLE);
    TIM_CCxChannelCmd(htim->Instance, step_motor[interpolation_para.active_axis].pul_channel, TIM_CCx_ENABLE);
  }
  
  /* 进给总步数减1 */
  interpolation_para.endpoint_pulse--;

  /* 判断是否完成插补 */
  if(interpolation_para.endpoint_pulse == 0)
  {
    /* 关闭定时器 */
    TIM_CCxChannelCmd(htim->Instance, step_motor[last_axis].pul_channel, TIM_CCx_DISABLE);
    TIM_CCxChannelCmd(htim->Instance, step_motor[interpolation_para.active_axis].pul_channel, TIM_CCx_DISABLE);
    __HAL_TIM_MOE_DISABLE(htim);
    HAL_TIM_Base_Stop_IT(htim);
  }
}

2.6 插补计算过程

用逐点比较插补法插补第一象限的直线OA，O点为原点，A点坐标为 （8，6），请完成以下任务：

（1）列出插补计算过程；

（2）画出插补轨迹图。

import numpy as np 
from matplotlib import pyplot as plt 
 
#确定第一象限直线
line = [[0, 8], [0, 6]]                            
plt.title("point-by-point relative method") 
plt.xlabel("X") 
plt.ylabel("Y") 
plt.plot(line[0],line[1]) 
plt.scatter(line[0], line[1], color='Red')
plt.show()

#计算出总共节拍
Nxy =abs((line[0][1]-line[0][0]))+abs((line[1][1]-line[1][0]))
print(Nxy)

Output:14

#F作为判别函数，S和E代表偏差与坐标值计算时候的xy轴
F = 0
S = [0,0]
E = [0,0]
print(end= "Step\tDiscriminant function\t")
print(end= "Feed function\tDeviation and coordinate value calculation\t")
print(end= "End point\n")
for i in range(0, Nxy):
    print(end = "{}\t".format(i+1))
    #判段判别函数，分别得出进给方向，偏差与坐标值计算
    if F >= 0:
        print(end = "F >= 0\t\t\t+X\t\t")
        F = F - line[1][1]
        print(end = "F = {}\t\t\t\t\t\t".format(F))
        S[1] = S[1] + 1
        plt.plot(S,E) 
        plt.scatter(S,E, color='b')
        S[0] = S[1]
        print(end = "{}\n".format(Nxy - i))
        continue
    
    if F < 0:
        print(end = "F < 0\t\t\t+Y\t\t")
        F = F + line[0][1]
        print(end = "F = {}\t\t\t\t\t\t".format(F))
        E[1] = E[1] + 1
        plt.plot(S,E) 
        plt.scatter(S,E, color='b')
        E[0] = E[1]
        print(end = "{}\n".format(Nxy - i))
        continue
 
#进行图像打印
plt.plot(line[0],line[1]) 
plt.scatter(line[0], line[1], color='Red')
plt.grid(color = 'gray')
plt.show()

Output