13_线性回归分析、线性模型、损失函数、最小二乘法之梯度下降、回归性能评估、sklearn回归评估API、线性回归正规方程，梯度下降API、梯度下降 和 正规方程对比

1.线性回归

1.1 线性模型

试图学得一个通过属性的线性组合来进行预测的函数：

1.2 定义

定义：线性回归通过一个或者多个自变量与因变量之间进行建模的回归分析。其中特点为一个或多个称为回归系数的模型参数的线性组合。

一元线性回归：涉及到的变量只有一个。
多元线性回归：涉及到的变量两个或两个以上。

要注意的是：预测结果与真实值是有一定的误差的。

单变量：

多变量：

1.3 损失函数(误差大小)

如何去求模型当中的W，使得损失最小？
（目的是找到最小损失对应的W值）

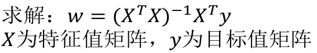
缺点：当特征过于复杂，求解速度太慢；对于复杂的算法，不能使用正规方程求解（逻辑回归等）

1.4 损失函数直观图（单变量举例）

1.5 最小二乘法之梯度下降（理解过程）

我们以单变量中的w0,w1为例子：


理解：沿着这个函数下降的方向找，最后就能找到山谷的最低点，然后更新W值。
使用：面对训练数据规模十分庞大的任务。

1.5 回归性能评估

（均方误差（Mean Squared Error）MSE）评价机制：

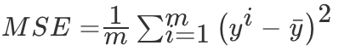
1.5.1 sklearn回归评估API

sklearn.metrics.mean_squared_error

mean_squared_error(y_true, y_pred)
    均方误差回归损失
    
    y_true   : 真实值
    y_pred   : 预测值
    return   :  浮点数结果

注意：真实值，预测值为标准化之前的值。

1.6 sklearn线性回归正规方程、梯度下降API

正规方程线性回归（Normal Equation）
优点：直接求解，且误差较小
缺点：当特征过多且过于复杂(维度>10000)时，求解速度太慢且得不到结果

sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False,copy_X=True, n_jobs=1)
通过正规方程优化

fit_intercept : 默认为True,是否计算该模型的偏置。如果使用中心化的数据，可以考虑设置为False,不考虑偏置。注意这里是考虑，一般还是要考虑偏置。
normalize : 默认为false。当fit_intercept设置为false的时候，这个参数会被自动忽略。如果为True,回归器会标准化输入参数：减去平均值，并且除以相应的二范数。当然啦，在这里还是建议将标准化的工作放在训练模型之前。通过设置sklearn.preprocessing.StandardScaler来实现，而在此处设置为false.
copy_X : 默认为True,否则X会被改写。
n_jobs : int默认为1.当-1时默认使用全部CPUs

可用属性：
coef_:如果输入的是多目标问题，则返回一个二维数组(n_targets, n_features)；如果是单目标问题，返回一个一维数组 (n_features,)
intercept_:偏置，线性模型中的独立项
rank_:矩阵X的秩，仅在X为密集矩阵时有效。   输出：矩阵X的秩
singular_:矩阵X的奇异值，仅在X密集矩阵时有效。

可用的methods:
fit(X,y,sample_weight=None):   训练模型，sample_weight为每个样本权重值，默认None
    X: array, 稀疏矩阵 [n_samples,n_features]
    y: array [n_samples, n_targets]
    sample_weight: 权重 array [n_samples]

get_params(self[,deep=True])：
    deep默认为True，返回一个字典，键为参数名，值为估计器参数值
    
predict(self,X):
    模型预测，返回预测值，预测基于R^2值
    
score(self,X,y[,sample_weight]):
    模型评估，返回R^2系数，最优值为1，说明所有数据都预测正确

set_params(self, **params)
    设置估计器的参数，可以修改参数重新训练

案例一：

# -*- coding: UTF-8 -*-

import sklearn
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

## 设置字符集，防止中文乱码
mpl.rcParams['font.sans-serif']=[u'simHei']
mpl.rcParams['axes.unicode_minus']=False

# 定义目标函数通过改函数产生对应的y
# y=1*x[0]+2*x[1]+....(n+1)*x[n]
def l_model(x):
    params = np.arange(1,x.shape[-1]+1)
    y = np.sum(params*x)+np.random.randn(1)*0.1
    return y

# 定义数据集
x = pd.DataFrame(np.random.rand(500,6))
y = x.apply(lambda x_rows:pd.Series(l_model(x_rows)),axis=1)

print(x)
print("--------------------------------------------")
print(y)
print("--------------------------------------------")

# 划分训练集和测试集
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.3,random_state=2)

# 数据标准化
ss = StandardScaler()
x_train_s = ss.fit_transform(x_train)
x_test_s = ss.transform(x_test)

# 输出下原数据的标准差和平均数
print(ss.scale_)
print(ss.mean_)

# 训练模型
lr = LinearRegression()
lr.fit(x_train_s,y_train)

print(lr.coef_)
print(lr.intercept_)

# 用模型预测
y_predict=lr.predict(x_test_s)
lr.score(x_test_s,y_test)

## 预测值和实际值画图比较
t = np.arange(len(x_test_s))
plt.figure(facecolor='w')   #建一个画布，facecolor是背景色
plt.plot(t, y_test, 'r-', linewidth=2, label='真实值')
plt.plot(t, y_predict, 'g-', linewidth=1, label='预测值')
plt.legend(loc = 'upper left') #显示图例，设置图例的位置
plt.title("线性回归预测真实值之间的关系",fontsize=20)
plt.grid(b=True) #加网格
plt.show()

输出结果：

           0         1         2         3         4         5
0    0.121430  0.769888  0.595199  0.753939  0.655383  0.456001
1    0.553240  0.813419  0.001539  0.577961  0.319791  0.621340
2    0.182807  0.050649  0.749899  0.838822  0.484833  0.086469
3    0.192126  0.830503  0.542332  0.031367  0.164466  0.905168
4    0.504114  0.267268  0.927765  0.532320  0.519348  0.820886
..        ...       ...       ...       ...       ...       ...
495  0.252219  0.710159  0.368021  0.383371  0.532386  0.783152
496  0.234624  0.356947  0.746875  0.466724  0.826973  0.748026
497  0.754129  0.086671  0.521319  0.397017  0.122910  0.363536
498  0.131987  0.627655  0.460967  0.217514  0.399104  0.352512
499  0.433256  0.185982  0.642580  0.014061  0.748104  0.219911
[500 rows x 6 columns]
--------------------------------------------
             0
0    12.307726
1     9.914944
2     8.726742
3     9.821706
4    13.433480
..         ...
495  11.766508
496  13.585479
497   6.747270
498   7.694877
499   7.956194
[500 rows x 1 columns]
--------------------------------------------
[0.29208501 0.29339293 0.28590121 0.29285606 0.28335227 0.30361955]
[0.49172956 0.50414285 0.48561849 0.48097964 0.48482669 0.47370829]
[[0.28845918 0.59197092 0.85958405 1.16537609 1.41842054 1.81026001]]
[10.14439954]

图：

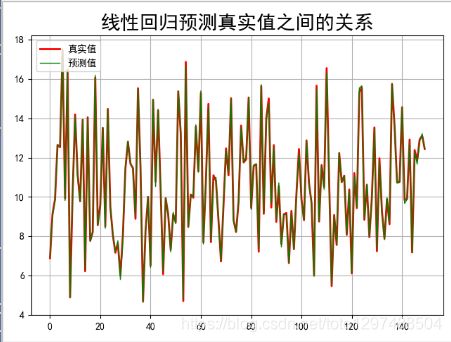
案例二：
https://blog.csdn.net/seagal890/article/details/105125566/

# -*- coding: utf-8 -*-

import matplotlib.pyplot as plt
from sklearn import datasets, linear_model, metrics
from sklearn.model_selection import train_test_split

# load the boston dataset
boston = datasets.load_boston(return_X_y=False)

# defining feature matrix(X) and response vector(y)
X = boston.data
y = boston.target

# splitting X and y into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)

# create linear regression object
reg = linear_model.LinearRegression()

# train the model using the training sets
reg.fit(X_train, y_train)

# regression coefficients
print('Coefficients: \n', reg.coef_)

# variance score: 1 means perfect prediction
print('Variance score: {}'.format(reg.score(X_test, y_test)))

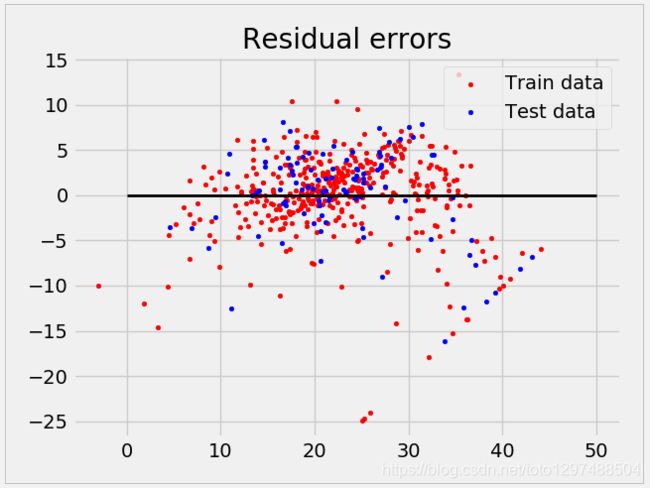
# plot for residual error

# setting plot style
plt.style.use('fivethirtyeight')

# plotting residual errors in training data
plt.scatter(reg.predict(X_train), reg.predict(X_train) - y_train, color="red", s=10, label='Train data')

# plotting residual errors in test data
plt.scatter(reg.predict(X_test), reg.predict(X_test) - y_test, color="blue", s=10, label='Test data')

# plotting line for zero residual error
plt.hlines(y=0, xmin=0, xmax=50, linewidth=2)

# plotting legend
plt.legend(loc='upper right')

# plot title
plt.title("Residual errors")

# function to show plot
plt.show()

输出结果：

Coefficients: 
 [-1.12386867e-01  5.80587074e-02  1.83593559e-02  2.12997760e+00
 -1.95811012e+01  3.09546166e+00  4.45265228e-03 -1.50047624e+00
  3.05358969e-01 -1.11230879e-02 -9.89007562e-01  7.32130017e-03
 -5.44644997e-01]
Variance score: 0.7634174432138463

图片结果：

案例三：

# -*- coding: utf-8 -*-

from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression, SGDRegressor,  Ridge, LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error,classification_report
from sklearn.externals import joblib

def mylinear():
    """
    线性回归直接预测房子价格
    :return:
    """
    # 获取数据
    lb = load_boston(return_X_y=False)

    # 分割数据集到训练集和测试集
    x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)
    print(y_train,y_test)

    # 进行标准化处理(?) 目标值处理？
    # 特征值和目标值是都必须进行标准化处理, 实例化两个标准化API
    std_x = StandardScaler()
    x_train = std_x.fit_transform(x_train)
    x_test = std_x.transform(x_test)

    # 目标值
    std_y = StandardScaler()
    # 下面会报：ValueError: Expected 2D array, got 1D array instead: 的错误，是因为python3的原因
    y_train = std_y.fit_transform(y_train)
    y_test = std_y.transform(y_test)

    # estimator预测
    # 正规方程求解方式预测结果
    lr = LinearRegression()
    lr.fit(x_train, y_train)
    print(lr.coef_)

    # 保存训练好的模型
    joblib.dump(lr, "./tmp/test.pkl")

    # 预测测试集的房子价格
    y_lr_predict = std_y.inverse_transform(lr.predict(x_test))

    print("正规方程测试集里面每个房子的预测价格：", y_lr_predict)
    print("正规方程的均方误差：", mean_squared_error(std_y.inverse_transform(y_test), y_lr_predict))


    # 预测房价结果
    # model = joblib.load("./tmp/test.pkl")
    # y_predict = std_y.inverse_transform(model.predict(x_test))
    # print("保存的模型预测的结果：", y_predict)

    return None

if __name__ == "__main__":
    mylinear()

随机梯度下降线性回归（Stochastic Gradient Descent,SGD）
优点：面对大量特征也能求得结果，且能够找到较好的结果。
缺点：速度相对较慢，需要多次迭代，且需要调整学习率，当学习率调整不当时，可能会出现函数不收敛的情况。

sklearn.linear_model.SGDRegressor(loss=’squared_loss’,fit_intercept=True,learning_rate=’invscaling’,eta0=0.01)
SGDRegressor类实现了随机梯度下降学习，它支持不同的loss函数和正则化惩罚项来拟合线性回归模型

loss:损失类型
    loss='squared_loss':普通最小二乘法
fit_intercept:是否计算偏置
learning_rate：string，optional
    学习率填充
    1、'constant':eta = eta0
    2、'optimal':eta=1.0 / (alpha * (t + t0)) [default]
    3、'invscaling':eta=eta0 / pow(t,power_t)
       power_t = 0.25 : 存在父类当中
    4、对于一个常数值的学习率来说，可以使用learning_rate=’constant’，并使用eta0来指定学习率。

SGDRegressor.coef_:回归系数
SGDRegressor.intercept_:偏置

案例：

# -*- coding: utf-8 -*-

from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression, SGDRegressor,  Ridge, LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error,classification_report
from sklearn.externals import joblib

def mylinear():
    """
    线性回归直接预测房子价格
    :return:
    """
    # 获取数据
    lb = load_boston(return_X_y=False)

    # 分割数据集到训练集和测试集
    x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)
    print(y_train,y_test)

    # 进行标准化处理(?) 目标值处理？
    # 特征值和目标值是都必须进行标准化处理, 实例化两个标准化API
    std_x = StandardScaler()
    x_train = std_x.fit_transform(x_train)
    x_test = std_x.transform(x_test)

    # 目标值
    std_y = StandardScaler()
    # 下面会报：ValueError: Expected 2D array, got 1D array instead: 的错误，是因为python3的原因
    y_train = std_y.fit_transform(y_train)
    y_test = std_y.transform(y_test)

    # 梯度下降去进行房价预测
    sgd = SGDRegressor()
    sgd.fit(x_train,y_train)
    print(sgd.coef_)

    # 预测测试集的房子价格
    y_sgd_predict = std_y.inverse_transform(sgd.predict(x_test))
    print("梯度下降测试集里面每个房子的预测价格：", y_sgd_predict)

    print("梯度下降的均方误差：", mean_squared_error(std_y.inverse_transform(y_test), y_sgd_predict))

    return None

if __name__ == "__main__":
    mylinear()

1.7 梯度下降 和 正规方程对比

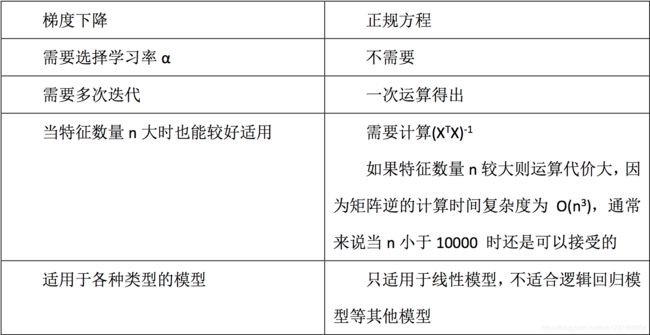
特点： 线性回归器是最简单，易用的回归模型。
线性回归器是最为简单、易用的回归模型。从某种程度上限制了使用，尽管如此，在不知道特征之间关系的前提下，我们仍然使用线性回归器作为大多数系统的首要选择。
小规模数据：LinearRegression(不能解决拟合问题)以及其它
大规模数据：SGDRegressor

打个赏呗，您的支持是我坚持写好博文的动力。