数据结构排序
整本书的知识点,点击右方链接:整本书笔记知识点
文章目录
- 八、排序
- 8.1、基本概念和排序方法概述
- 8.1.1、排序的基本概念
- 8.1.2、内部排序方法的分类
- 8.1.3、待排序记录的存储方式
- 8.2、插入排序
- 8.2.1、直接插入排序
- 8.8.2、折半插入排序
- 8.2.3、希尔排序
- 8.3、交换排序
- 8.3.1、冒泡排序
- 8.3.2、快速排序
- 8.4、选择排序
- 8.4.1、简单选择排序
- 8.4.2、树形选择排序
- 8.4.3、堆排序
- 8.5、归并排序
- 8.6、基数排序
- 8.7、外部排序
- 8.7.1、外部排序的基本方法
- 8.7.2、多路平衡归并
- 8.7.3、置换-选择排序
- 8.7.4、最佳归并树
- 第八章小结
- 第八章习题
八、排序
8.1、基本概念和排序方法概述
8.1.1、排序的基本概念
-
排序 :就是一系列数据,按照某个关键字(例如:销量,价格),进行递增或者递减的顺序排列起来
-
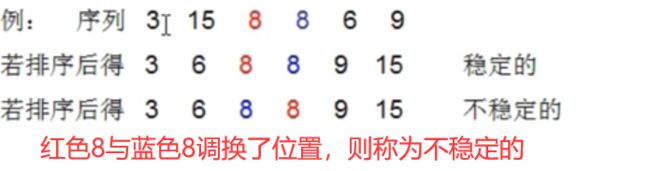
排序的稳定性 :能保证两个关键字相等的数,经过排序之后,其在序列的前后位置顺序不变。(A1=A2,排序前A1在A2前面,排序后A1还在A2前面),则称这种排序是稳定的。反之,若排序后前后位置顺序变化,则称这种排序是不稳定的
-
内部排序和外部排序 :待排序记录全部存放在计算机内存中进行排序的过程称为内部排序;在排序过程中需对外存进行访问的排序过程
-
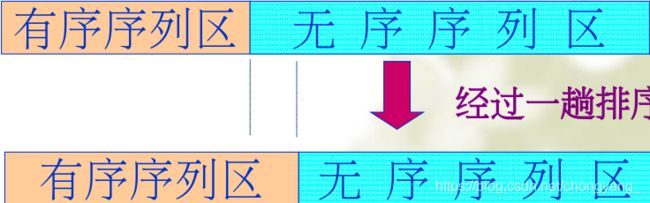
内部排序的过程是一个逐步扩大记录的有序序列长度的过程
8.1.2、内部排序方法的分类
内部排序的方法很多,每一种方法都有各自的优点,适合在不同环境下使用
将排序记录分为:有序序列区和无序序列区
![]()
8.1.3、待排序记录的存储方式
- 顺序表:实现排序需要移动记录
- 链表:实现排序不需要移动记录,仅需修改指针即可。这种排序方式称为链表排序
- 地址排序:在排序过程中不移动记录本身,而移动地址向量这些记录的“地址”,在排序结束之后再按照地址向量中的值调整记录的存储位置
8.2、插入排序
8.2.1、直接插入排序
![]()
把待排序的数据插入到已经排好序的数据中,直到所有的数据插入完成,即就是直接插入排序。
![]()
为了避免数组下标出界,在 r[0] 处设置监视哨
void InsertSort(SqList &L) {
//从第二个数开始选择循环,第一个数默认当做已排序状态
for (int i = 2; i <= L.length; ++i) {
//当 当前数小于前一个数的时候,进入if判断
if (L.r[i].key < L.r[i - 1].key) {
//将此数暂存到监视哨中
L.r[0] = L.r[i];
//前一个数后移,空出前一个数的位置,看上面的gif
L.r[i] = L.r[i - 1];
//第二层循环,用于比较此数与已排序状态中各个数的大小
//上面判断过此数小于前一个数,所以直接 j=i-2
//若r[j]是最小的数,则当j=0的时候,会退出循环
for (j = i - 2; L.r[0].key < L.r[j].key; --j) {
//当此数比L.r[j]小时,L.r[j]后移,空出位置以便此数插入
L.r[j + 1] = L.r[j];
}
//第二层循环结束,将监视哨中的原值插入到正确的位置
L.r[j + 1] = L.r[0];
}
}
}
时间复杂度:平均O(n^2),最好O(n), 最坏O(n^2)
空间复杂度:O(1),因为只需要一个记录的辅助空间 r[0]
特点:
- 稳定性:稳定
- 也适用于链式存储结构,只是在单链表上无需移动记录,只需修改相应的指针
- 更适用与初始化基本有序的情况
8.8.2、折半插入排序
**原理:**折半插入算法是对直接插入排序算法的改进,排序原理同直接插入算法
**区别:**以从小到大排序为例,首先用key存储需要排序的数据
第一步:折半查找——用low、mid、high划分两个区域【low,mid-1】和【mid+1,high】
第二步:判断——如果key值小于序列的中间值【mid】,则代表key值应该插入左边的区域【low,mid-1】,然后对【low,mid-1】再重复划分区域,直到low>high为止
第三步:插入——最后的插入位置应该是high+1,我们只需要先将high之后位置的数据整体后移,然后将key赋值给【mid+1】,即完成插入。
![]()
转载于:折半插入排序
时间复杂度:O(n2)
空间复杂度:仍是只需要一个记录的辅助空间r[0],所以时间复杂度为O(1)
特点:
- 稳定性:稳定
- 因为要进行折半查找,所以只能用于顺序结构,不能用于链式结构
- 适合初始记录无序、n较大的时候
8.2.3、希尔排序
![]()
希尔排序又称为“缩小增量排序”。
看了很多笔记,总觉得文字讲解冗杂难懂。不如这个视频
六分钟讲解希尔排序
最后的增量一定为1,同一组中使用直接插入排序。
![]()
时间复杂度:n(log2n)2
空间复杂度:也是只需要一个辅助空间 r[0] ,所以时间复杂度为O(1)
特点:
- 稳定性:因为记录跳跃式地移动,所以不稳定
- 只适用于顺序结构,不能用于链式结构
- 适用于初始记录无序、n较大的情况
8.3、交换排序
8.3.1、冒泡排序
![]()
(1)第一次比较:首先比较第一和第二个数,将小的数放在前面,将大的数放在后面。
(2)比较第2和第3个数,将小数放在前面,大数放在后面。
…
(3)如此继续,直到比较到最后的两个数,将小数放在前面,大数放在后面,重复步骤,直至全部排序完成
(4)在上面一趟比较完成后,最后一个数一定是数组中最大的一个数,所以在比较第二趟的时候,最后一个数是不参加比较的。
(5)在第二趟比较完成后,倒数第二个数也一定是数组中倒数第二大数,所以在第三趟的比较中,最后两个数是不参与比较的。
(6)依次类推,每一趟比较次数减少
![]()
时间复杂度为O(n2),但若是一开始就是有序的,则时间复杂度为O(n)
特点:
- 稳定性:稳定
- 可以用于链式存储结构
- 当初始记录无序,n较大时,此算法不宜采用
8.3.2、快速排序
严奶奶中的快速排序算法过程和《算法导论》中的过程不太一样,虽然最后结果一样。找了好多笔记,迷茫了好大一会。这里按照严奶奶的方法写过程了。
当选择枢轴关键字的记录是第一个关键字时,则从最右边开始先向左寻找;当选择枢轴关键字是最后一个关键字时,则从最左边开始向右寻找。
![]()
然后小于46的那一半再按照此方法排序,右边那一半也按照此方法排序,直到划分完所有关键字
做图太累啦哈哈哈哈哈哈哈,我自己手写了剩余过程,我以后一定练字!!!!
![]()
看了很多笔记,看起来很难理解,看这个八分钟视频很容易理解快速排序的概念
八分钟理解快速排序
时间复杂度:O(nlog2n)
空间复杂度:最好情况下的空间复杂度为:O(log2n),最坏情况下为O(n)
特点:
- 记录非顺次的移动导致排序方法是不稳定的
- 排序过程中需要定位表的下界和上界,所以适合用于顺序结构,很难用于链式结构
- 当n较大时,在平均情况下快速排序是所有内部排序方法中速度最快的一种,所以其适合初始记录无序、n较大时的情况
8.4、选择排序
8.4.1、简单选择排序
gif讲解,最小值与前面第一个未排序状态交换
![]()
简单选择排序又称为直接选择排序
在要排序的一组数中,选出最小(或者最大)的一个数与第1个位置的数交换;然后在剩下的数中再找最小(或者最大)的与第2个位置的数交换,以此类推,直到 第n-1个元素(倒数第二个数)和第n个元素(最后一个数)比较为止。
简单选择排序的实例:
![]()
时间复杂度:O(n2)
空间复杂度:同冒泡排序一样,只有在两个记录交换时需要一个辅助空间,所以空间复杂度为O(1)
特点:
- 稳定性:就选择排序方法来讲是稳定的,但教程中实现的方法是不稳定的
- 可用于链式存储结构
- 移动记录次数较少,当每一记录占用的空间较多时,此方法比直接插入排序快
8.4.2、树形选择排序
树形选择排序,又称锦标赛排序(理解即可)
转载于,又做了些更改树形选择排序
从两个节点中选出最小值作为他们的父节点
![]()
缺点: 1、与“∞”的比较多余; 2、辅助空间使用多。于是产生了堆排序
8.4.3、堆排序
以下图转载于:堆排序
堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。如下图:
![]()
同时,我们对堆中的结点按层进行编号,将这种逻辑结构映射到数组中就是下面这个样子
![]()
该数组从逻辑上讲就是一个堆结构,我们用简单的公式来描述一下堆的定义就是:
大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
ok,了解了这些定义。接下来,我们来看看堆排序的基本思想及基本步骤:
堆排序基本思想及步骤
堆排序的基本思想是:将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了
步骤一 构造初始堆。将给定无序序列构造成一个大顶堆(一般升序采用大顶堆,降序采用小顶堆)。
a.假设给定无序序列结构如下
![]()
b.此时我们从下至上,从右到左找非叶子结点,转换为父节点大于子节点的状态
![]()
c.找到第二个非叶节点4,由于[4,9,8]中9元素最大,4和9交换。
![]()
这时,交换导致了子根[4,5,6]结构混乱,继续调整,[4,5,6]中6最大,交换4和6。
![]()
此时,我们就将一个无需序列构造成了一个大顶堆。
步骤二 将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换。
a.将堆顶元素9和末尾元素4进行交换,并且将9标记为已排序状态
![]()
b.重新调整结构,使其继续满足堆定义
![]()
c.再将堆顶元素8与末尾元素5进行交换,得到第二大元素8,并将8也标记为已标记状态
![]()
后续过程,继续进行调整,交换,如此反复进行,最终使得整个序列有序
![]()
再简单总结下堆排序的基本思路:
a.将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
b.将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
c.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
我觉得笔记讲的太冗杂,找到了个视频感觉不错,时长在十分钟,讲的很慢,二倍速听也能跟上
十分钟讲解堆排序
时间复杂度:O(nlog2n)
空间复杂度:O(1)
特点:
- 稳定性:不稳定排序
- 只能用于顺序结构,不能用于链式结构
- 记录较少时不宜采用
8.5、归并排序
![]()
七分钟讲解归并排序
归并排序是用分治思想,分治模式在每一层递归上有三个步骤:
- 分解(Divide):将n个元素分成个含n/2个元素的子序列
- 解决(Conquer):用合并排序法对两个子序列递归的排序
- 合并(Combine):合并两个已排序的子序列已得到排序结果
转载于归并排序
![]()
再来看看治阶段,我们需要将两个已经有序的子序列合并成一个有序序列,比如上图中的最后一次合并,要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列,合并为最终序列[1,2,3,4,5,6,7,8],来看下实现步骤。
比较 i 和 j (即两组中各自的第一个元素),将小的元素放入到temp中
![]()
![]()
8.6、基数排序
从最低位(个位)开始进行,按关键字的不同收集,然后按第二低位(十位)开始进行,按关键字的不同收集,若有些数没有更低位,则按0收集
特点:
- 稳定性:稳定排序
- 可用于链式结构,也可用于顺序结构
- 基数排序需要知道各级关键字的取值范围
8.7、外部排序
8.7.1、外部排序的基本方法
转自外部排序定义讲解
当我们要排序的文件太大以至于内存无法一次性装下的时候,这时候我们可以使用外部排序,将数据在外部存储器和内存之间来回交换,以达到排序的目的
一天晚上,徒弟正在呆呆地看着星星,师傅突然坐在了他的旁边。
师傅:徒弟啊,天上的星星那么多,不妨你给他们按大小排个序吧。
徒弟:哦,这个怎么排?
师傅:具体到我们的编程,就是给你2G的数据在硬盘上,但是你只有256M的内存可以使用,怎么排这2G的数据呢?
徒弟:这么小的内存,装不下数据啊,怎么排呢?
师傅:还记得分而治之的思想吗?我们可以采用这种思想把它排好序。
徒弟:具体怎么做呢?
首先我们可以将2G的数据分成8份,分别加载到内存中进行排序,在内存中的排序方法可以用内部排序如快排、希尔等,如下图:
![]()
这些已经排好序的数据块我们称之为顺串或者归并段
![]()
然后我们可以将两个顺串通过内存合并成一个顺串(长度为原来的两倍),经过四次合并就完成了。
注意:合并操作几乎不需要内存,只需要读入两个元素,选择一个最大的(或最小的)输出,然后再读入,再选择
![]()
按照这个方法一直来回合并,一直合并到最终的一个顺串(有序),此时排序完成。
举个实际的例子吧:
为了简化,设待排数据为:80,92,12,97,13,34,18,98,27,57,40,74,内存一次可以装三个数据。
![]()
将数据分为四段:
![]()
然后将每段读入内存,排序后写入硬盘
![]()
然后两两合并
![]()
输出哪个元素,就在那个元素所在的顺串(或者叫组)再次读入元素
![]()
![]()
就这样,一直合并到两个顺串完,如果一个顺串先完,剩下另一个顺串,那么就将剩下的顺串直接拷贝到硬盘上。
按照这个方法,把合并后的顺串继续合并,直到最终合并成一个总的顺串,排序结束。
![]()
徒弟:我听说硬盘的读写速度比内存要慢的多,按照这种排序那岂不是很慢。
师傅:好问题,一般我们会从两方面去优化。
对同一个文件而言,采取这种排序方法所需读写外存(磁盘)的次数与归并趟数有关,很容易理解,归并趟数越多,内存和外存的交互次数就越多。
假设初始时有 m 个顺串,每次对 k 个顺串进行归并,归并趟数就为:
![]()
比如我们的例子,刚开始的时候顺串(初始顺串)有 4 个(m=4),每次对 2 个顺串进行归并(k=2),那么归并趟数就为:
![]()
到此,我们优化的目标就很明确了:
① 增加归并的顺串数量 k
② 减少初始顺串的个数 m
8.7.2、多路平衡归并
【归并排序】归并排序不需要将全部记录都读入内存即可完成排序,是外部排序中最常用的方法
| 内部排序的归并算法 | 外部排序的归并算法 | 相同点 |
|---|---|---|
| 子序列存在内存中 | 子序列在外存中(文件中) | 思想一样,都是从小单元归并到单元 |
之前是两两一合并,使得归并顺串的数量为 2(这叫2-路平衡归并), 我们可以多归并几个,这样我们就可以减少归并的趟数了,从而减少外存的读写次数
以刚才的例子来看,这次我们假设内存大小可以容纳四个元素,我们一次对4个顺串进行归并(4-路平衡归并)
![]()
这样只需要一次合并就可以了,外存读写次数为24(12读+12写),比之前的48少了一半,于此同时我们也可以看到需要更大的内存了,内存之中选出最大值也会更耗时,所以要权衡选 k。
在内存之中选最大(或最小)值时,可以选择一个元素与其他元素一个一个比,然后更新最值,但是效率会比较低,一般采取败者树来选择
在外部排序方法中,为了减少I/O次数,而需要将二路平衡归并改为多路平衡归并,但是按照原有的归并算法,将二路归并改为多路归并将增加其内部排序的时间。为了是内部排序不受到归并数目的影响,从而引入了败者树的概念。
概念:败者树是对树形选择排序的一种变化,它是一颗完全二叉树。每个叶子节点存放各个归并段在当前位置需要参加归并的记录,其内部节点用来记录左右子数中的“失败者”,从而让胜利者继续比较,一直到根节点。根据需求可以将左右子数中大的(小的)定义为失败者,小的(大的)为胜利者,则根节点指向的数为最小数(最大数)。
下面以大的为失败者,小的为胜利者解释。
![]()
败者留在双亲结点,胜者继续向上比较
如上图所示:有b0、b1、b2、b3、b4五个归并路数,它们的值分别是10、9、20、6、12.首先看b3和b4比较,b3为胜利者,于是将失败者b4的路号4存入b3、b4的父节点中;将胜利者b3继续与b0相比,b3对应的是6,b4对应的是10,于是b3为胜利者,b0为失败者,将失败者b0的路号0存入到上一层父节点中;再看右边b1和b2的比较,b1对应的是9,b2对应的是20,于是b1为胜利者,b2为失败者,将失败者b2的路号2存入到b1、b2的父节点中;然后将左边的胜者b3与右边的胜者b1比较,b3对应的是6,b1对应的是9,则b3为胜者,b1为败者,将失败者b1的路号1存入到上一层父节点中;最后在将胜利者的路号写入ls[0]中。
8.7.3、置换-选择排序
置换-选择排序和最佳归并树实在不知道怎么用笔记描述,看下面的一个十分钟视频应该可以理解这两个思想
上一节介绍了增加 k-路归并排序中的 k 值来提高外部排序效率的方法,而除此之外,还有另外一条路可走,即减少初始归并段的个数,也就是本章中提到的减小 m 的值
m 的求值方法为:m=⌈n/l⌉(n 表示为外部文件中的记录数,l 表示初始归并段中包含的记录数)
感觉这个视频讲解的也十分清晰
十四分钟讲解置换-选择排序 最佳归并树
8.7.4、最佳归并树
其实就是哈夫曼树,上面的视频链接也有讲
某个元素的I/O次数就是权值 * 2
第八章小结
![]()
![]()
第八章习题
(1)从未排序序列中依次取出元素与已排序序列中的元素进行比较,将其放入已排序序列的正确位置上的方法,这种排序方法称为
A.归并排序 B.冒泡排序 C.插入排序 D.选择排序
答案:C
(2)从未排序序列中挑选元素,并将其依次放入已排序序列(初始时为空)的一端的方法,称为( )。
A.归并排序 B.冒泡排序 C.插入排序 D.选择排序
答案:D
(3)对n个不同的关键字由小到大进行冒泡排序,在下列( )情况下比较的次数最多。
A.从小到大排列好的 B.从大到小排列好的
C.元素无序 D.元素基本有序
答案:B
解释:对关键字进行冒泡排序,关键字逆序时比较次数最多。
(4)对n个不同的排序码进行冒泡排序,在元素无序的情况下比较的次数最多为( )。
A.n+1 B.n C.n-1 D.n(n-1)/2
答案:D
解释:比较次数最多时,第一次比较n-1次,第二次比较n-2次……最后一次比较1次,即(n-1)+(n-2)+…+1= n(n-1)/2。
(5)快速排序在下列( )情况下最易发挥其长处。
A.被排序的数据中含有多个相同排序码
B.被排序的数据已基本有序
C.被排序的数据完全无序
D.被排序的数据中的最大值和最小值相差悬殊
答案:C
解释:B选项是快速排序的最坏情况。
(6)对n个关键字作快速排序,在最坏情况下,算法的时间复杂度是( )。
A.O(n) B.O(n2) C.O(nlog2n) D.O(n3)
答案:B
解释:快速排序的平均时间复杂度为O(nlog2n),但在最坏情况下,即关键字基本排好序的情况下,时间复杂度为O(n2)。
(7)若一组记录的排序码为(46, 79,56,38,40,84),则利用快速排序的方法,以第一个记录为基准得到的一次划分结果为
A.38,40,46,56,79,84 B.40,38,46,79,56,84
C.40,38,46,56,79,84 D.40,38,46,84,56,79
答案:C
按照视频中的方法讲解即可清楚,看我花的图也行
(8)下列关键字序列中,( )是堆。
A.16,72,31,23,94,53 B.94,23,31,72,16,53
C.16,53,23,94,31,72 D.16,23,53,31,94,72
答案:D
解释:D选项为小根堆
(9)堆是一种( )排序。
A.插入 B.选择 C.交换 D.归并
答案:B
(10)堆的形状是一棵( )。
A.二叉排序树 B.满二叉树 C.完全二叉树 D.平衡二叉树
答案:C
(11)若一组记录的排序码为(46,79,56,38,40,84),则利用堆排序的方法建立的初始堆为( )。
A.79,46,56,38,40,84 B.84,79,56,38,40,46
C.84,79,56,46,40,38 D.84,56,79,40,46,38
答案:B
(12)下述几种排序方法中,要求内存最大的是( )。
A.希尔排序 B.快速排序 C.归并排序 D.堆排序
答案:C
解释:堆排序、希尔排序的空间复杂度为O(1),快速排序的空间复杂度为O(log2n),归并排序的空间复杂度为O(n)。
(13)下述几种排序方法中,( )是稳定的排序方法。
A.希尔排序 B.快速排序 C.归并排序 D.堆排序
答案:C
解释:不稳定排序有希尔排序、简单选择排序、快速排序、堆排序;稳定排序有直接插入排序、折半插入排序、冒泡排序、归并排序、基数排序。
(14)数据表中有10000个元素,如果仅要求求出其中最大的10个元素,则采用( )算法最节省时间。
A.冒泡排序 B.快速排序 C.简单选择排序 D.堆排序
答案:D
(15)下列排序算法中,( )不能保证每趟排序至少能将一个元素放到其最终的位置上。
A.希尔排序 B.快速排序 C.冒泡排序 D.堆排序
答案:A
解释:快速排序的每趟排序能将作为枢轴的元素放到最终位置;冒泡排序的每趟排序能将最大或最小的元素放到最终位置;堆排序的每趟排序能将最大或最小的元素放到最终位置。
2.应用题
(1)设待排序的关键字序列为{12,2,16,30,28,10,16*,20,6,18},试分别写出使用以下排序方法,每趟排序结束后关键字序列的状态。
① 直接插入排序
![]()
② 折半插入排序
折半插入排序中的排序功能其实就是直接插入排序,则同①
③ 希尔排序(增量选取5,3,1)
![]()
④ 冒泡排序
![]()
⑤ 快速排序
![]()
⑥ 简单选择排序
![]()
⑦ 堆排序
堆排序画图太复杂,而且不难,可以直接写一下
⑧ 二路归并排序
![]()