线索二叉树之后序线索化

目录

前言

温故知新

后序线索化思路

代码实现

后序线索化代码

后序线索二叉树遍历

三叉链的节点结构

遍历思路

代码实现

示例程序

 主函数代码

运行结果

---

前言

线索二叉树以及线索化的概念，节点改造请见博客：线索二叉树剖析【C/C++】

先序线索二叉树算法思路及代码实现请看：线索二叉树之先序线索化

本文将介绍后序线索化二叉树的算法思路以及代码实现

---

温故知新

线索化的实质就是将二叉链表中的空指针改为指向前驱或后继的线索。由于前驱和后继的信息只有在遍历该二叉树时才能得到，所以线索化的过程就是在遍历的过程中修改空指针的过程。

也就是说，我们只对含孩子指针为空的节点进行改造

后序线索化思路

1、算法整体结构仍是一个后序遍历，只不过遍历过程中对空指针进行改造

2、空指针改造无非指向前驱或者后继，所以我们需要一个指向前驱节点的指针prev

3、对于待改造节点，如果左孩子为空，那么我们需要把它指向当前节点的前驱节点，并且标记左孩子为线索节点

4、对于待改造节点，如果右孩子为空，那么我们需要把它指向当前节点的前驱节点，并且标记右孩子为线索节点

5、当前节点改造完毕，我们需要依次改造仍为非线索节点的左子树右子树

代码实现

后序线索化代码

有没有发现无论是中序线索化还是先序线索化都是在中序/先序遍历中加入了相同的操作

void PostThreading(BiThrNode *root, BiThrNode *&prev) // 主程序调用该函数时prev为nullptr
{
    if (!root)
        return;
    PostThreading(root->_left, prev); // 递归线索化左子树

    PostThreading(root->_right, prev); // 递归线索化右子树
    if (!root->_left)
    {
        // 当前节点左为空，则当前节点左指向前驱也就是prev
        root->_left = prev;
        root->_ltag = PointerTag::Thread;
    }
    if (prev != nullptr && !(prev->_right))
    // 前驱节点右为空，则前驱节点指向后继也就是root
    // 前驱节点的左已经在前驱节点的线索化函数内处理过了
    {
        prev->_right = root;
        prev->_rtag = PointerTag::Thread;
    }
    prev = root;
}

后序线索二叉树遍历

对于后序线索二叉树的遍历，单纯靠我们节点的left指针和right指针就无法实现了，因为我们对于后序遍历，一个节点它的左右子树遍历完毕后遍历完自身后是要遍历父亲节点或者父亲的右子树，但是如果右节点为非线索节点的话是无法跳到父节点和其子树的，对此我们有两种方案，一种是像二叉树非递归遍历那样借助栈，不过较为复杂，我们选择改造节点结构为三叉链结构，即添加一个_parent指针来指向父亲节点

三叉链的节点结构

typedef char TElemType;
struct BiThrNode
{
    BiThrNode(const TElemType &data, PointerTag ltag = PointerTag::Link, PointerTag rtag = PointerTag::Link)
        : _left(nullptr), _right(nullptr), _parent(nullptr), _data(data), _ltag(ltag), _rtag(rtag)
    {
    }
    // 指针域
    BiThrNode *_left;
    BiThrNode *_right;
    BiThrNode *_parent;
    // 数据域
    TElemType _data;
    // 孩子/后继标识
    PointerTag _ltag;
    PointerTag _rtag;
};

遍历思路

1、后序遍历到一个节点，他有两种情况，右子树还没遍历以及右子树遍历完毕回溯到该节点，为了区分两种情况我们需要加一个prev指针，如果右节点为prev，那么我们遍历完当前节点就得眺到_parent

2、对于每颗子树我们要找到该子树的后序遍历首节点，而由于我们加了prev指针，所以转化为找到左节点为线索节点且指向prev的节点

3、找到后序首节点后按照右线索节点一直遍历，当我们遍历到一个右节点为非线索节点的节点，则有两种情况，该节点为根节点，那么我们遍历根节点直接退出，另一种是当前子树的根节点，我们按照1、中的操作进行即可

代码实现

void PostOrderTraverse_Thr(BiThrNode *root)
{
    if (!root)
        return;
    BiThrNode *cur = root;
    BiThrNode *prev = nullptr;
    while (cur)
    {
        // 找到prev的下一个节点
        while (cur->_left != prev)
            cur = cur->_left;
        // 当_ltag为Link就找到了当前子树中序遍历第一个节点
        // 按照后继节点遍历
        while (cur && cur->_rtag == PointerTag::Thread)
        {
            cout << cur->_data << " ";
            prev = cur;
            cur = cur->_right;
        }
        if (cur == root)
        {
            cout << cur->_data << " ";
            return;
        }
        // 当只要右子树访问完了就往父亲走
        while (cur && cur->_right == prev)
        {
            cout << cur->_data << " ";
            prev = cur;
            cur = cur->_parent;
        }
        // 右子树为线索节点则进行访问
        if (cur && cur->_rtag == PointerTag::Link)
        {
            cur = cur->_right;
        }
    }
}

示例程序

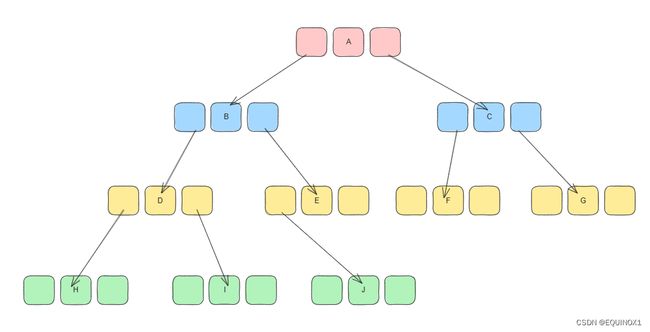
仍以该二叉树为例

 主函数代码

int main()
{
    // 构建示例图二叉树
    BiThrNode *root = Create_BTTree();
    // 线索化前的后序遍历
    cout << "线索化前的后序遍历"
         << ":   ";
    PostOrder(root);

    // 线索化后的后序遍历
    BiThrNode *prev = nullptr;

    PostThreading(root, prev);
    cout << "线索化后的后序遍历"
         << ":   ";
    PostOrderTraverse_Thr(root);
    return 0;
    // A B D H 0 0 I 0 0 E J 0 0 0 C F 0 0 G 0 0
}

运行结果