快速排序全面详解
目录
1 基本思想
2 排序步骤
3 代码实现
3.1 区间划分算法(hoare初始版本):
3.2 主框架
4 区间划分算法
4.1 hoare法
4.2 挖坑法
4.3 前后指针法
5 快排优化
5.1 取key方面的优化
5.2 递归方面的优化
5.3 区间划分方面的优化
6 快排非递归实现
6.1 栈实现(代码+图解)
6.2 队列实现
7 特性总结
1 基本思想
快速排序采用分治法,任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
2 排序步骤
-
选取基准值,通过区间划分算法把待排序序列分割成左右两部分。
-
左右序列中递归重复1。
3 代码实现
3.1 区间划分算法(hoare初始版本):
区间划分算法有三个版本:hoare法,挖坑法,前后指针法,这里介绍hoare法,也是快排的初始划分法。
三种划分方法的结果可能不同,但都是让小的值往前靠拢,大的值往后靠拢,让整个序列逐渐趋于有序。
步骤:
默认序列最左边的元素为基准值key,设置left,right指针;
left找大,right找小,right要先找,都找到后交换a[left]和a[right];
重复步骤3
当left == right时,交换key和相遇位置的元素,完成分割。
走完这一趟后,key值左边都不比key大,key值右边都不比key小,key值到了他排序后应该在的位置,不需要挪动这个元素了。
图解:
![]()
算法分析:
为什么能保证相遇位置的值一定比key值小,然后交换?
关键点就是让right先找!
相遇有两种情况:
left往right靠拢,与right相遇:right先找到了小的元素,相遇后的值一定比key小。
right往left靠拢,与left相遇:left指针指向的元素是上一波交换过后的元素,该元素比key小。
假如我们让left先找的话,相遇位置比key值大,不能交换。
代码:
int Partion(int* a, int left, int right)
{
int keyI = left;
//left == right两个指针相遇,退出循环
while (left < right)
{
//right先找,right找小
while (left < right && a[right] >= a[keyI])
{
right--;
}
//left找大
while (left < right && a[left] <= a[keyI])
{
left++;
}
//都找到了,交换
Swap(&a[left], &a[right]);
}
//left和right相遇,交换key和相遇位置元素
Swap(&a[keyI], &a[left]);
return left;
}划分方法一般不用hoare,是因为这种算法实现的代码很容易出现bug,比如:
key值一般取最左边或者最右边的值,但是要注意key不能用变量保存,而是要保存key的下标keyI,否则最后key与相遇位置的交换并没有真正交换数组中的key。(注意:有些划分算法是用变量保存key,有些是保存下标keyI,视情况而定。)
right找小和left找大的过程中,要保证left < right,否则可能出现数组越界,比如1,9,6,4,2,7,8,2 ;右边的值都比key大,会导致越界。
a[right] >= a[keyI]或者a[left] <= a[keyI]时,才能--right或者++left;如果是a[right] > a[keyI]或者a[left] < a[keyI]可能出现死循环,比如a[left] == a[right] == key时,交换完后不进入内部while,外部while陷入死循环。
3.2 主框架
void _QuickSort(int* a, int begin, int end)
{
if (begin >= end)
return;
//根据基准值把数组划分成左右序列
int keyI = Partion(a, begin, end);
//左右序列递归划分下去
_QuickSort(a, begin, keyI - 1);
_QuickSort(a, keyI + 1, end);
}
void QucikSort(int* a, int n)
{
_QuickSort(a, 0, n - 1);
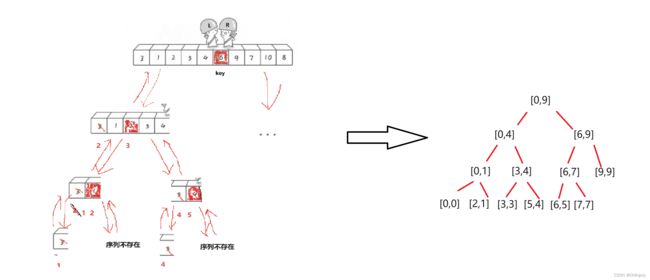
}上述为快速排序递归实现的主框架,与二叉树前序遍历规则非常像。
二叉树的递归终止条件是空树,快排的终止条件是数组只有一个元素(left==right)或者数组区间不存在(left>right)。
浅画一下展开图:
4 区间划分算法
前面所说,hoare划分法有一定的缺陷,我们再介绍其他两种常用的划分方法。
4.1 hoare法
int Partion(int* a, int left, int right)
{
int keyI = left;
//left == right两个指针相遇,退出循环
while (left < right)
{
//right先找,right找小
while (left < right && a[right] >= a[keyI])
{
right--;
}
//left找大
while (left < right && a[left] <= a[keyI])
{
left++;
}
//都找到了,交换
Swap(&a[left], &a[right]);
}
//left和right相遇,交换key和相遇位置元素
Swap(&a[keyI], &a[left]);
return left;
}4.2 挖坑法
步骤:
默认序列最左边的元素为基准值key,把值挖走用key变量保存,该位置为一个坑。
右边找小,找到后把值填给坑位,该位置成为新的坑位。
左边找大,找到后把值填给坑位,该位置成为新的坑位。
重复步骤2~3。
左右相遇,相遇位置也是个坑位,key值填入坑位。
图解:
代码:
int Partion2(int* a, int left, int right)
{
int key = a[left];
int hole = left;
while (left < right)
{
while (left < right && a[right] >= key)
{
right--;
}
a[hole] = a[right];
hole = right;
while (left < right && a[left] <= key)
{
left++;
}
a[hole] = a[left];
hole = left;
}
a[hole] = key;
return hole;
}与前面代码不同的是,这里的key值我们不存下标,用一个变量保存。
4.3 前后指针法
步骤:
默认序列最左边的元素为基准值key,设置prev指针 == left,cur指针 == left+1。
cur找小,找到后,prev++,a[prev]和a[cur]交换。
重复步骤2。
cur走完以后,a[prev]和key交换。
图解:
代码:
int Partion3(int* a, int left, int right)
{
int keyI = left;
int prev = left, cur = prev + 1;
while (cur <= right)
{
if (a[cur] < a[keyI] && ++prev != cur)
Swap(&a[prev], &a[cur]);
++cur;
}
Swap(&a[prev], &a[keyI]);
return prev;
}为了避免自己和自己交换,prev先++判断和cur是否相等,相等就不交换。
很明显这种分割方法的代码相比前面两种简单了许多,这种划分法也是最常用的。
5 快排优化
5.1 取key方面的优化
最理想的情况就是key值每次都是中间的值,快排的递归就是一个完美的二分。
快排在面对一些极端数据时效率会明显下降;就比如完全有序的序列,这种序列的基准值key如果再取最左边或者最右边的数,key值就是这个序列的最值,复杂度会变成O(N^2):
![]() 这时候就可以用三数取中法来解决这个弊端,三个数为:a[left],a[mid],a[right],这样就可以尽量避免key值选到最值的情况。
这时候就可以用三数取中法来解决这个弊端,三个数为:a[left],a[mid],a[right],这样就可以尽量避免key值选到最值的情况。
//三数取中法选key值
int GetMidIndex(int* a, int left, int right)
{
int mid = (left + right) / 2;
if (a[left] < a[mid])
{
if (a[mid] < a[right])
return mid;
else if (a[left] > a[right])
return left;
else
return right;
}
else //mid < left
{
if (a[left] < a[right])
return left;
else if (a[mid] > a[right])
return mid;
else
return right;
}
}
//前后指针划分
int Partion3(int* a, int left, int right)
{
//中间值的下标为midI,a[left]替换为此中间值
int midI = GetMidIndex(a, left, right);
Swap(&a[left], &a[midI]);
int keyI = left;
int prev = left, cur = prev + 1;
while (cur <= right)
{
if (a[cur] < a[keyI] && ++prev != cur)
Swap(&a[prev], &a[cur]);
++cur;
}
Swap(&a[prev], &a[keyI]);
return prev;
}除了三数取中法,我们还可以考虑随机数法,都能在一定程度上避免这种极端情况。
srand((unsigned int)time(NULL));
//前后指针划分
int Partion3(int* a, int left, int right)
{
//随机数取key
int keyI = left + rand() % (right - left + 1);
Swap(&a[left], &a[keyI]);
int keyI = left;
int prev = left, cur = prev + 1;
while (cur <= right)
{
if (a[cur] < a[keyI] && ++prev != cur)
Swap(&a[prev], &a[cur]);
++cur;
}
Swap(&a[prev], &a[keyI]);
return prev;
}5.2 递归方面的优化
我们知道,递归深度太深并不是一件好事,所以我们可以针对递归方面来进行优化,减少绝大多数的递归调用。
如何优化呢?当递归到区间内元素个数<=10时,调用直接插入排序。
void _QuickSort(int* a, int begin, int end)
{
if (begin >= end)
return;
//区间内元素个数 <= 10,调用直接插入排序
if (end - begin + 1 <= 10)
{
InsertSort(a + begin, end - begin + 1);
//注意:起始地址是a + begin,不是a
}
else
{
//根据基准值把数组划分成左右序列
int keyI = Partion3(a, begin, end);
//左右序列递归划分下去
_QuickSort(a, begin, keyI - 1);
_QuickSort(a, keyI + 1, end);
}
}这种优化其实可以减少绝大多数的递归调用,我们把快排的递归划分想象成一颗二叉树,区间长度小于10的数组大概在这棵二叉树的最后三层,而最后三层占了整棵树结点个数的80%多(最后一层50%,倒数第二层25%...),类比快排的递归来看,我们省去了80%多的递归调用,并且对于数据规模较小的情况下,直插和快排的效率差不了多少,所以这是一个极大的优化,算法库中的sort函数也大多是这种优化。
5.3 区间划分方面的优化
快排针对某些极端数据,效率会下降至O(N^2),这种极端数据我们前面说过:
完全有序的序列算是一个,
还有一种极端数据就是数组中某个元素(我们称为x)大量出现,甚至数组中全部都是一个元素x。
针对情况一,我们可以优化取key来解决这个问题,针对情况二,这种方法不奏效。
那么我们可以从区间划分算法下手:
以前的区间划分算法(前后指针法)是双路划分,也就是一遍走完之后,数组被划分成[left, keyI - 1], keyI, [keyI + 1, right]三部分,左区间 < key, 右区间 >= key,然后左右两个区间再递归划分下去;
这种划分方法有一个弊端,就是x大量出现时(甚至整个数组都是一种元素x),会导致左右区间的元素数量严重失衡,导致快排效率下降。
这里我们就可以使用三路划分了,所谓三路划分,就是数组被划分成三部分:< key、==key、 和> key三个部分,我们只需递归划分
key这两部分的区间。 由于key值很容易取到x(一旦取到x,左右区间的size一定会大大减小),这种算法一定程度上提高了效率。
如何实现?详见LeetCode912:
class Solution {
public:
pair Partion(vector& nums, int begin, int end)
{
//随机数取key
int keyI = begin + rand() % (end - begin + 1);
swap(nums[begin], nums[keyI]);
int key = nums[begin];
int left = begin, right = end, cur = left + 1;
while(cur <= right)
{
if(nums[cur] < key)
{
swap(nums[left++], nums[cur++]);
}
else if(nums[cur] == key)
{
cur++;
}
else
{
swap(nums[right--], nums[cur]);
}
}
return make_pair(left, right);
}
void QuickSort(vector& nums, int begin, int end)
{
if(end - begin + 1 <= 1)
return;
pair p = Partion(nums, begin, end);
QuickSort(nums, begin, p.first - 1);
QuickSort(nums, p.second + 1, end);
}
vector sortArray(vector& nums)
{
srand((unsigned int)time(NULL));
QuickSort(nums, 0, nums.size() - 1);
return nums;
}
}; 6 快排非递归实现
快排的非递归我们可以使用一个栈(深度优先遍历)或者一个队列实现(广度优先遍历)。
6.1 栈实现(代码+图解)
void QuickSortNonRByStack(int* a, int n)
{
Stack st;
StackInit(&st);
int begin = 0, end = n - 1;
//先Push右边界,在Push左边界
//记住push顺序,取top的时候左右不要取反了
StackPush(&st, end);
StackPush(&st, begin);
while (!StackEmpty(&st))
{
int begin = StackTop(&st);
StackPop(&st);
int end = StackTop(&st);
StackPop(&st);
int keyI = Partion3(a, begin, end);
//[begin, keyI - 1] keyI [keyI + 1, end]
//先递归到左区间,所以右区间先入栈
if (keyI + 1 < end)
{
//先Push右边界,在Push左边界
StackPush(&st, end);
StackPush(&st, keyI + 1);
}
if (begin < keyI - 1)
{
//先Push右边界,在Push左边界
StackPush(&st, keyI - 1);
StackPush(&st, begin);
}
}
StackDestory(&st);
}
![]()
6.2 队列实现
void QuickSortNonRByQueue(int* a, int n)
{
Queue q;
QueueInit(&q);
int begin = 0, end = n - 1;
QueuePush(&q, begin);
QueuePush(&q, end);
while (!QueueEmpty(&q))
{
int begin = QueueFront(&q);
QueuePop(&q);
int end = QueueFront(&q);
QueuePop(&q);
int keyI = Partion3(a, begin, end);
if (begin < keyI - 1)
{
QueuePush(&q, begin);
QueuePush(&q, keyI - 1);
}
if (keyI + 1 < end)
{
QueuePush(&q, keyI + 1);
QueuePush(&q, end);
}
}
QueueDestory(&q);
}7 特性总结
-
快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
-
时间复杂度:O(NlogN)
最好情况,每次key都在中间位置,正好二分
最坏情况,每次key都是最值,复杂度O(N^2)
平均情况(带优化),复杂度O(NlogN)
-
空间复杂度:O(logN)