LeetCode1314. 矩阵区域和

题目：

1314.矩阵区域和
给你一个 m x n 的矩阵 mat 和一个整数 k ，请你返回一个矩阵 answer ，其中每个 answer[i][j] 是所有满足下述条件的元素 mat[r][c] 的和：

• i - k <= r <= i + k, j
• k <= c <= j + k 且
• (r, c) 在矩阵内。

示例 1：

输入：mat = [[1,2,3],[4,5,6],[7,8,9]], k = 1
输出：[[12,21,16],[27,45,33],[24,39,28]]

示例 2：

输入：mat = [[1,2,3],[4,5,6],[7,8,9]], k = 2
输出：[[45,45,45],[45,45,45],[45,45,45]]

思路：
1.暴力求解

2.可以使用行/列前缀和优化内层暴力求解区间和

求和的正方形的边界优化：

• 由于 i - k < ０　或　i + k >= m，因此行最大的有效区间是[max(i - k, 0), min(i + k, m -1)]
• 由于 j - k < ０　或　j + k >= n，因此列最大的有效区间是[max(j - k, 0), min(ij+ k, n -1)]

1.行前缀和优化：rowPrefix[i][j]表示第 i 行 ，[0,j]列的和

• 由于在求解第 i 行，[j1,j2]列的和时，使用rowPrefix[i][j2] - rowPrefix[i][j1 - 1]时遇到 j1 - 1 < 0,因此实际使用时会将前缀和数组索引向右偏移一个单位。
• 即 rowPreflix[i][j] 代表的是原数组中，第 i 行 [0, j -1]列的和。

2.列前缀和优化：colPrefix[i][j]表示第 j 列 ，[0, i]行的和

• 由于在求解第 j 行，[i1,i2]列的和时，使用colPrefix[i2][j] - rowPrefix[i1 - 1][j]时遇到 i1 - 1 < 0,因此实际使用时会将前缀和数组索引向右偏移一个单位。
• 即 rowPreflix[i][j] 代表的是原数组中，第 j 列 [0, i -1]行的和。

代码：

class Solution {
public:
    vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {
        int m = mat.size();
        int n = mat[0].size();
        vector<vector<int>> rowPrefix(m, vector<int>(n + 1, 0));
        //计算行前缀和
        for(int i = 0; i < m; i++) {
            for(int j = 1; j <= n; j++) {
                rowPrefix[i][j] = rowPrefix[i][j - 1] + mat[i][j - 1];
            }
        }
        //对[j - k, j + k]列之和相加
        vector<vector<int>> ans(m, vector<int>(n, 0));
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                for(int r = max(i-k, 0); r <= min(i+k, m-1); r++) {
                    ans [i][j] += rowPrefix[r][min(j+k, n-1) + 1] - rowPrefix[r][max(j - k, 0)];
                }
            }
        }
        return ans;
    }

};

复杂度分析：

• 时间复杂度： O(mnk) ,优化一维查询速度
• 空间复杂度：创建前缀和数组为O(mn)

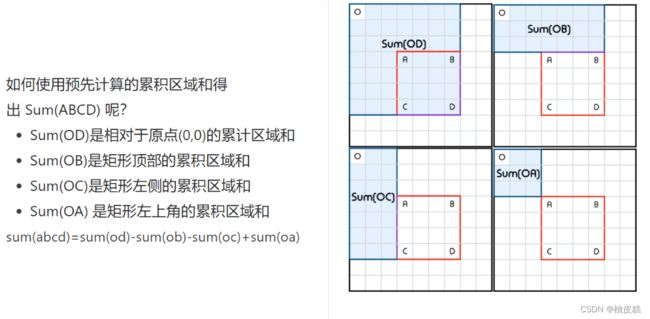
3.方块面积相减（二维前缀和）右下角减左上角矩形

代码：

class Solution {
public:
    vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {
        int m = mat.size();
        int n = mat[0].size();
        vector<vector<int>> prefix(m + 1, vector<int>(n + 1, 0));
        for(int i = 1; i <= m; i++) {
            for(int j = 1; j <= n; j++) {
                prefix[i][j] = prefix[i - 1][j] + prefix[i][j - 1] - prefix[i - 1][j - 1] + mat[i - 1][j - 1];
            }
        }

        vector<vector<int>> ans(m, vector<int>(n, 0));
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                int row1 = max(i - k, 0), col1 = max(j - k, 0);
                int row2 = min(i + k, m - 1), col2 = min(j + k, n - 1);
                ans[i][j] = prefix[row2 + 1][col2 + 1] - prefix[row1][col2 + 1] - prefix[row2 + 1][col1] + prefix[row1][col1];
            }
        }
        return ans;
    }

};

复杂度分析：

• 时间复杂度：创建二维前缀和数组为O(mn)，求和为O(mn)。
• 空间复杂度：创建二维前缀和数组为O(mn)。