LeetCode 1314. 矩阵区域和--前缀和
- 矩阵区域和
给你一个 m x n 的矩阵 mat 和一个整数 k ,请你返回一个矩阵 answer ,其中每个 answer[i][j] 是所有满足下述条件的元素 mat[r][c] 的和:
i - k <= r <= i + k,
j - k <= c <= j + k 且
(r, c) 在矩阵内。
示例 1:
输入:mat = [[1,2,3],[4,5,6],[7,8,9]], k = 1
输出:[[12,21,16],[27,45,33],[24,39,28]]
示例 2:
输入:mat = [[1,2,3],[4,5,6],[7,8,9]], k = 2
输出:[[45,45,45],[45,45,45],[45,45,45]]
提示:
m == mat.length
n == mat[i].length
1 <= m, n, k <= 100
1 <= mat[i][j] <= 100
题解
累计前缀和,dp[x][y]表示矩形[0-x,0-y]的区域和,那么我们的答案就是:
画图说明吧:
假设S1的右下角坐标为(x1,y1),S2的右下角坐标为(x2,y2),S3的右下角坐标为(x3,y3),目标区域和的右下角坐标为(x4,y4)。

S1+S2+S3+目标区域和=dp[x4][y4]
那么此时
S3+目标区域和=dp[x4][y4]-dp[x2-1][y2]
S3=dp[x3][y3]-dp[x1][y1]
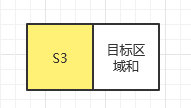
此时目标区域和=dp[x4][y4]-dp[x2-1][y4]-(dp[x3][y3]-dp[x1][y1])
AC代码
class Solution {
public:
int dp[105][105];
vector<vector<int>>res;
vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int K)
{
memset(dp,0,sizeof(dp));
for(int i=0;i<mat.size();i++)
{
int ans=0;
for(int j=0;j<mat[i].size();j++)
{
ans+=mat[i][j];
dp[i+1][j+1]=dp[i][j+1]+ans;
}
}
for(int i=1;i<=mat.size();i++)
{
vector<int>row;
for(int j=1;j<=mat[0].size();j++)
{
int x1,y1,x2,y2,x3,y3,x4,y4;
x1=min(i+K,int(mat.size())),y1=min(j+K,int(mat[0].size()));
x2=max(i-K,1),y2=min(j+K,int(mat[0].size()));
x3=min(i+K,int(mat.size())),y3=max(j-K,1);
x4=max(i-K,1),y4=max(j-K,1);
row.push_back(dp[x1][y1]-dp[x2-1][y2]-(dp[x3][y3-1]-dp[x4-1][y4-1]));
}
res.push_back(row);
}
return res;
}
};