【故障诊断】用于轴承故障诊断的候选故障频率优化克改进包络频谱研究（Matlab代码实现）

欢迎来到本博客❤️❤️

博主优势：博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

本文目录如下：

目录

1 概述

2 运行结果

3 参考文献

4 Matlab代码实现

---

1 概述

该文讲解一种基于候选故障频率优化克（IESCFFOgram）的改进包络频谱的特征自适应方法，用于从频谱相干性（SCoh）中识别信息 频谱频段，以进行轴承故障诊断。在新方法中，根据SCoh的局部特征自动识别候选故障频率（CFF），而不是标称故障特性频率（FCF）， 并进一步用于指导信息频段的选择。 这种新方法完全摆脱了对FCF或稀疏性指标的依赖，可以通过 挖掘隐藏在SCoh平面中的故障信息，自适应地生成诊断IES。 因此，所提出的IESCFFOgram适用于在没有准确FCF的情况下滚动轴承的故障识别。还提供用于估计光谱相关性（或光谱相干性）的快速算法。
用于检测和分析循环平稳信号。

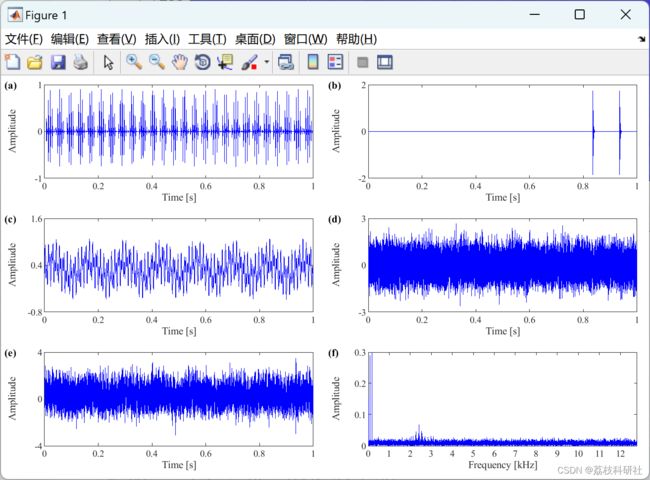
2 运行结果

 

 

 

 

 

部分代码：

%% Load Simlated Inner race fault signal
load('SimInner');
Sigplot = SimInner;

%% Basic parameters
Fs = 12800*2;     % Sampling Frequency
N = 1*Fs ;        % Sampling Length
t  = 0 : 1/Fs : (N-1)/Fs ;  % Time
f_m = 142 ;       % Bearing fault charatersitic fraquency
f_shaft = 26;

%% Plot the raw signal components and the frequency spectrum of the mixed signal
% Frequency spectrum of the mixed siganl
nfft = 2*ceil(length(Sigplot(:,5))/2); Freraw = Fs*(0:nfft/2-1)/nfft;
env = Sigplot(:,5);  
% env = abs(hilbert(Sigplot(:,5))); 
Han = hanning(length(env)); Han = Han(:); 
EnvSpec = abs(fft(((env-mean(env)).^1).*Han,nfft)); 
EnvSpec = EnvSpec./max(EnvSpec);
EnvSpec(nfft/2+1:end) = []; 

% Figure
figure(1)
subplotnum_1 = 3;
subplotnum_2 = 2; 
leftleave = 0.067;
upleave = 0.005;
downleave = 0.082;
step_1 = (1-0-upleave)/subplotnum_1;
step_2 = 1/subplotnum_2;
plotheight = step_1*0.70; 
plotwidth = step_2*0.83;   
str = {'(a)','(b)','(c)','(d)','(e)','(f)'};
set (gcf,'unit','centimeters','Position',[12 15 14 8.5], 'color','w'); % 脥录脝卢脦禄脰脙 麓贸脨隆
for i = 1 : subplotnum_1
    for j = 1 : subplotnum_2
        if (i-1)*2+j <6
            plotx = t';
            ploty = Sigplot( : , (i-1)*2+j  );
        else
            plotx =  Freraw/1000;
            ploty = EnvSpec*0.3;
        end
        subplot(subplotnum_1,subplotnum_2, (i-1)*subplotnum_2+j)
        plot( plotx , ploty, 'b' );     % ylabel('Amplitude');
        set(gca,'unit','normalized','Position',[leftleave+(j-1)*step_2   downleave+(subplotnum_1-i)*step_1  plotwidth*1 plotheight*1]);
        figure_FontSize = 7; set(gca,'Fontsize',figure_FontSize,'Fontname','Times New Roman');
        if (i-1)*2+j  == 1
            set(gca,'ytick',[-1 0 1]); set(gca,'ylim',[-1  1]);
            yt = 1;ys = 0;
        elseif (i-1)*2+j  == 2
            set(gca,'ytick',[-2 :2: 2]); set(gca,'ylim',[-2  2]);
            yt = 2;ys = 0;
        elseif (i-1)*2+j  == 3
            set(gca,'ytick',[-0.8 0.4 1.6]); set(gca,'ylim',[-0.8  1.6]);
            yt = 1.6;ys = 0.4;
        elseif (i-1)*2+j  == 4
            set(gca,'ytick',[-3 0 3]); set(gca,'ylim',[-3  3]);
            yt = 3; ys = 0;
        elseif (i-1)*2+j  == 5
            set(gca,'ytick',[-4 0 4]); set(gca,'ylim',[-4  4]);
            yt = 4; ys = 0;   
        elseif (i-1)*2+j  == 6
            set(gca,'ytick',[0 :0.1 : 0.3]); set(gca,'ylim',[0  0.3]);
            yt = 0.3; ys = 0.15;
        end
        if (i-1)*2+j  < 6
            set(gca,'xtick',[0: 0.2: 1]); set(gca,'xlim',[0  1]);
             xlabel('Time [s]');  
             ylabel('Amplitude','Position',[-0.10*1 ys]);
             xt = -0.15*1; 
        else
            set(gca,'xtick',[0: 1: Fs/2/1000]); set(gca,'xlim',[0 Fs/2/1000]);
            xlabel('Frequency [kHz]');
            ylabel('Amplitude','Position',[-0.10*Fs/2/1000 ys]);
            xt = -0.15*Fs/2/1000;
        end
        text(xt,yt,str{(i-1)*2+j},'Fontname','Times New Roman','FontSize',8,'FontWeight','bold')

3 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1]Yao Cheng, Shengbo Wang, Bingyan Chen, Guiming Mei, Weihua Zhang, Han Peng, Guangrong Tian, "An Improved Envelope Spectrum via Candidate Fault Frequency Optimization-gram for Bearing Fault Diagnosis", Journal of Sound and Vibration,Elsevier, 2022.

[2]徐秀芳,徐丹妍,徐森,郭乃瑄,许贺洋.一种结合谱聚类与关联规则的轴承故障诊断方法[J].计算机测量与控制,2023,31(01):51-58.DOI:10.16526/j.cnki.11-4762/tp.2023.01.008.

4 Matlab代码实现