PostgreSQL中的索引——4（B树）

目录

B树

架构

通过等式搜索

通过不等式搜索

通过范围查询

示例

---

（本文中所述的B树通过双向链表组织了叶节点，其实应该算B+树）

我们已经讨论了PostgreSQL的索引引擎和访问方法的接口，以及哈希索引（一种访问方法）。现在我们将考虑最传统以及使用最广泛的索引——B树。文章很长，所以有点耐心。

B树

架构

B树索引类型，实现为“btree”访问方法，适用于可以排序的数据。换句话说，数据类型必须定义的大于、大于等于、小于、小于等于和等于操作。注意，相同的数据有时可以有不同的排序方法，操作符族中提到过这一点。

通常，B树索引行被打包到页面中。在叶页面中，这些行包含要索引的数据（键）和对表行的引用（TID）。在内部页面中，每一行指向索引的孩子页面，并包含孩子页面中的最小值。

B-树有几个重要特征：

B树是平衡树，即每个叶页与根页之间的内部页数相同。因此，搜索任何值都需要相同的时间。

B树是多叉树，即，每个页面（通常为8KB）包括很多TID（几百个），所以，B树的深度很小，对于非常大的表，树的深度只有4~5左右。

索引中的数据是按非递减顺序排序的（不论是在页面间还是每个页面内），同一级别的页面通过双向列表相互连接。因此，我们可以通过一个列表遍历一个或另一个方向来获得一个有序的数据集，而不必每次都返回到根。

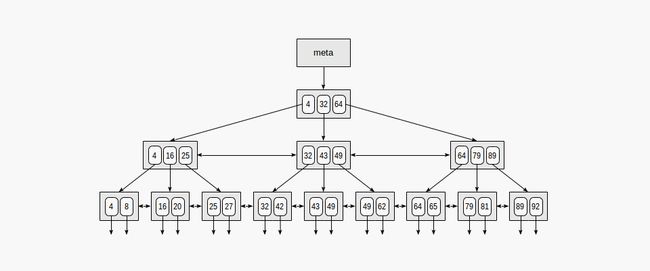
下面是一个带整数键的字段索引的简化示例。

索引最开始的页面为元页面，指向索引根节点。内部节点分布在根节点下，叶页面在最底行。从叶节点向下的箭头指向表行（TID）。

通过等式搜索

让我们考虑通过条件"indexed-field=expression"来在树中检索一个值，比如，我们想要找为49的键。

搜索从根节点开始，然后我们需要确定降到哪个子节点。知道根节点的键为（4,32,64）之后，我们就能找出子节点的值范围。因为32≤49≤64，我们应该降到第二个子节点上。接着，递归重复相同的操作，直到我们到达一个叶节点，从中可以获得所需的TID。

实际上，许多细节使这个看似简单的过程变得复杂。例如，一个索引可以包含非唯一键，并且可以有很多相等的值，以至于它们不适合一个页面（就是可能有很多个49，他们指向的TID不在一个页面上）。回到我们的例子，我们似乎应该从内部节点开始，对49的值进行引用。但是，从图中可以清楚地看到，这种索引方法中我们跳过了中间节点的“49”键。因此，一旦我们在一个内部页面中找到了一个完全相同的键，我们就必须向左下降一个位置，然后从左到右查看底层的索引行，以搜索所需的键。（为什么会跳过，因为中间节点它只存储键，没有向下指向TID的指针吧）

（另一个复杂的问题是，在搜索过程中，其他过程可能会更改数据：比如重建树，页面会被拆分为两个，等等。所有算法都是为这些并发操作设计的，它们不会相互干扰，也不会在可能的情况下导致额外的锁。但我们没打算在这方面进行扩展。）

通过不等式搜索

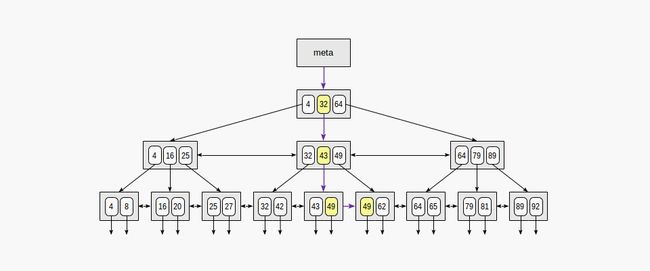
当通过条件“indexed-field≤expression”（或者indexed-field≥expression）进行搜索时，我们首先通过等式条件“indexed field=expression”在索引中找到一个值（如果有），然后沿着适当的方向遍历叶页直到结束。

图片说明了n≤35的过程：

同样的方式也支持大于、小于操作符，但必须删除最初找到的值。

通过范围查询

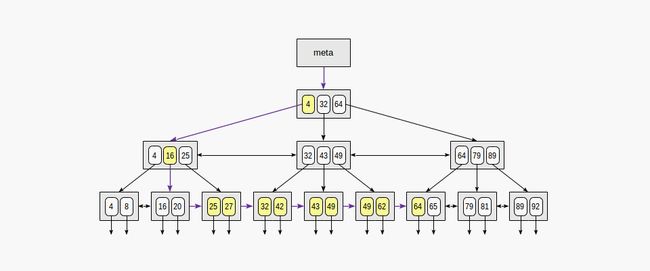
按范围“expression1”≤ indexed-field≤ expression2”搜索时，我们通过条件“indexed-field= expression1”找到一个值，然后，继续遍历满足条件“indexed field≤expression2”的叶页；或者反向操作：从第二个表达式开始，朝相反的方向走，直到值满足第一个表达式。

该图展示了条件 23≤n≤64 的检索过程:

示例

让我们看一个查询计划的例子。像之前一样，我们使用演示数据库，这次我们会考虑飞机表。它只包含九行，规划器（在扫描时）会选择不使用索引，因为整个表适合在一页中存储。但出于说明的目的，这张表对我们来说很有趣。

demo=# select * from aircrafts;

aircraft_code |        model        | range 
---------------+---------------------+-------
 773           | Boeing 777-300      | 11100
 763           | Boeing 767-300      |  7900
 SU9           | Sukhoi SuperJet-100 |  3000
 320           | Airbus A320-200     |  5700
 321           | Airbus A321-200     |  5600
 319           | Airbus A319-100     |  6700
 733           | Boeing 737-300      |  4200
 CN1           | Cessna 208 Caravan  |  1200
 CR2           | Bombardier CRJ-200  |  2700
(9 rows)


demo=# create index on aircrafts(range);

demo=# set enable_seqscan = off;

（或者指明“使用btree（range）在飞机上创建索引”，但它默认情况下构建的就是B树。）

通过等式搜索：

demo=# explain(costs off) select * from aircrafts where range = 3000;

                    QUERY PLAN                     
---------------------------------------------------
 Index Scan using aircrafts_range_idx on aircrafts
   Index Cond: (range = 3000)
(2 rows)

通过不等式搜索

demo=# explain(costs off) select * from aircrafts where range < 3000;

                    QUERY PLAN                    
---------------------------------------------------
 Index Scan using aircrafts_range_idx on aircrafts
   Index Cond: (range < 3000) 
(2 rows)

通过范围索引：

demo=# explain(costs off) select * from aircrafts
where range between 3000 and 5000;

                     QUERY PLAN                      
-----------------------------------------------------
 Index Scan using aircrafts_range_idx on aircrafts
   Index Cond: ((range >= 3000) AND (range <= 5000))
(2 rows)

排序

让我们再次强调一点，对于任何类型的扫描（索引、仅索引或位图），“btree”访问方法都会返回有序数据，这点我们可以在上图中清楚地看到。

因此，如果表在排序条件上有索引，优化器将考虑两个选项：表的索引扫描，它容易地返回排序的数据，以及对结果进行后续排序的，表的顺序扫描。

排序顺序

创建索引时，我们可以显式指定排序顺序。例如，我们可以通过以下方式创建航班范围索引：

demo=# create index on aircrafts(range desc);

在这种情况下，较大的值将出现在左侧的树中，而较小的值将出现在右侧。但如果我们可以在两个方向上遍历索引值的话，为什么还需要这样做呢？

其目的是建立多列索引。让我们创建一个视图，展示按常规划分为短程、中程和远程飞行器的飞机模型：

demo=# create view aircrafts_v as
select model,
       case
           when range < 4000 then 1
           when range < 10000 then 2
           else 3
       end as class
from aircrafts;

demo=# select * from aircrafts_v;

        model        | class
---------------------+-------
 Boeing 777-300      |     3
 Boeing 767-300      |     2
 Sukhoi SuperJet-100 |     1
 Airbus A320-200     |     2
 Airbus A321-200     |     2
 Airbus A319-100     |     2
 Boeing 737-300      |     2
 Cessna 208 Caravan  |     1
 Bombardier CRJ-200  |     1
(9 rows)

让我们创建一个两列索引（使用表达式）（第一列是表达式值1/2/3，第二列为text类型的model，它会自动根据由a到z的顺序建索引）：

demo=# create index on aircrafts(
  (case when range < 4000 then 1 when range < 10000 then 2 else 3 end),
  model);

现在，我们可以使用此索引以两列升序对数据进行排序：

demo=# select class, model from aircrafts_v order by class, model;

 class |        model        
-------+---------------------
     1 | Bombardier CRJ-200
     1 | Cessna 208 Caravan
     1 | Sukhoi SuperJet-100
     2 | Airbus A319-100
     2 | Airbus A320-200
     2 | Airbus A321-200
     2 | Boeing 737-300
     2 | Boeing 767-300
     3 | Boeing 777-300
(9 rows)

demo=# explain(costs off)
select class, model from aircrafts_v order by class, model;

                       QUERY PLAN                       
--------------------------------------------------------
 Index Scan using aircrafts_case_model_idx on aircrafts
(1 row)

类似地，我们可以执行查询以降序排列数据：

demo=# select class, model from aircrafts_v order by class desc, model desc;

 class |        model        
-------+---------------------
     3 | Boeing 777-300
     2 | Boeing 767-300
     2 | Boeing 737-300
     2 | Airbus A321-200
     2 | Airbus A320-200
     2 | Airbus A319-100
     1 | Sukhoi SuperJet-100
     1 | Cessna 208 Caravan
     1 | Bombardier CRJ-200
(9 rows)

demo=# explain(costs off)
select class, model from aircrafts_v order by class desc, model desc;

                           QUERY PLAN                            
-----------------------------------------------------------------
 Index Scan BACKWARD using aircrafts_case_model_idx on aircrafts
(1 row)

但是，我们不能使用此索引来获取按一列降序排列的数据，而按另一列升序排列的数据。这需要单独排序（查询计划中使用了顺序扫描，而不是索引扫描）：

demo=# explain(costs off)
select class, model from aircrafts_v order by class ASC, model DESC;

                   QUERY PLAN                    
-------------------------------------------------
 Sort
   Sort Key: (CASE ... END), aircrafts.model DESC
   ->  Seq Scan on aircrafts
(3 rows)

（请注意，作为最后一种手段，计划器选择顺序扫描，而不考虑之前设置的“enable_seqscan= off”。这是因为该设置实际上并不禁止表格扫描，而是将设置其为天文成本——请查看带有“costs on”的计划。）

要使此查询使用索引扫描，必须使用所需的排序方向构建索引：

demo=# create index aircrafts_case_asc_model_desc_idx on aircrafts(
 (case
    when range < 4000 then 1
    when range < 10000 then 2
    else 3
  end) ASC,
  model DESC);

demo=# explain(costs off)
select class, model from aircrafts_v order by class ASC, model DESC;

                           QUERY PLAN                            
-----------------------------------------------------------------
 Index Scan using aircrafts_case_asc_model_desc_idx on aircrafts
(1 row)

列的顺序

使用多列索引时出现的另一个问题是在索引中列出列的顺序。对于B-树，这个顺序非常重要：页面内的数据将按第一个字段排序，然后按第二个字段排序，依此类推。

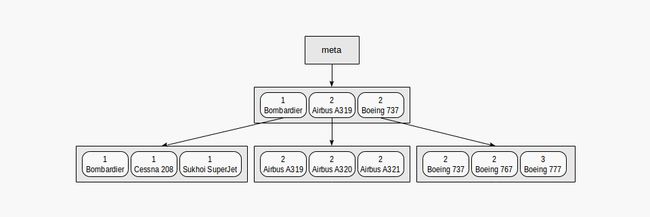
我们可以用符号的方式表示基于区间和模型的指数，如下所示： 

实际上，这么小的索引肯定能只在一个根页面中存下。在图中，为了清晰起见，特意将其分布在多个页面中。

从这张图表中可以清楚地看出，通过“class=3”（仅按第一个字段搜索）或“class=3和model= 'Boeing 777-300'（按两个字段搜索）这样的谓词进行搜索将非常有效。

然而，通过谓词“model='Boeing 777-300'”进行搜索的效率要低得多：因为从根节点开始，我们无法确定要下降到哪个子节点，因此，我们必须下降到所有子节点。但这并不意味着像这样的索引永远不能被使用——它的效率是个问题。例如，如果我们有三个等级的飞机，每个等级有很多型号，我们需要查看大约三分之一的索引，这可能比完整的表扫描更有效，也或者不是。

但是，如果我们创建这样的索引：

demo=# create index on aircrafts(
  model,
  (case when range < 4000 then 1 when range < 10000 then 2 else 3 end));

字段的顺序将更改：

有了这个索引，按谓词“model='Boeing 777-300'”进行搜索将有效，但按谓词“class=3”进行搜索将效率低下。

NULL值

“btree”访问方法能索引NULL值，并支持按条件为NULL和不为NULL进行搜索。

让我们考虑一下当NULL值出现时的航班：

demo=# create index on flights(actual_arrival);
demo=# explain(costs off) select * from flights where actual_arrival is null;

                      QUERY PLAN                       
-------------------------------------------------------
 Bitmap Heap Scan on flights
   Recheck Cond: (actual_arrival IS NULL)
   ->  Bitmap Index Scan on flights_actual_arrival_idx
         Index Cond: (actual_arrival IS NULL)
(4 rows)

空值位于叶节点的一端或另一端，具体取决于索引的创建方式（先空值或后空值）。如果查询包含排序，这一点很重要：如果SELECT命令在order BY子句中指定的空值顺序与为生成索引指定的顺序相同（先空值或后空值），则可以使用索引。

在以下示例中，这些顺序是相同的，因此，我们可以使用索引：

demo=# explain(costs off)
select * from flights order by actual_arrival NULLS LAST;

                       QUERY PLAN                      
--------------------------------------------------------
 Index Scan using flights_actual_arrival_idx on flights
(1 row)

下面，这些顺序是不同的，优化器选择顺序扫描然后排序：

demo=# explain(costs off)
select * from flights order by actual_arrival NULLS FIRST;

               QUERY PLAN              
----------------------------------------
 Sort
   Sort Key: actual_arrival NULLS FIRST
   ->  Seq Scan on flights
(3 rows)

要在这种情况下使用索引，必须在创建索引时指定将NULL值放在开头：

demo=# create index flights_nulls_first_idx on flights(actual_arrival NULLS FIRST);

demo=# explain(costs off)
select * from flights order by actual_arrival NULLS FIRST;

                     QUERY PLAN                      
-----------------------------------------------------
 Index Scan using flights_nulls_first_idx on flights
(1 row)

这样的问题是由NULL不可排序引起的，也就是说，NULL和任何其他值的比较结果是未定义的：

demo=# \pset null NULL
demo=# select null < 42;

 ?column?
----------
 NULL
(1 row)

这与B-树的概念背道而驰，不符合一般模式。然而，空值在数据库中扮演着如此重要的角色，我们总是不得不为它们设置例外。

因为空值可以被索引，所以即使没有对表施加任何条件，也可以使用索引（因为索引肯定包含所有表行的信息）。如果查询需要数据排序，并且索引确保了所需的顺序，那么这可能是有意义的。在这种情况下，规划器可以选择索引访问来保存单独的排序。

属性

让我们看看“btree”访问方法的属性（前面的文章已经提供了查询方法）。

 amname |     name      | pg_indexam_has_property
--------+---------------+-------------------------
 btree  | can_order     | t
 btree  | can_unique    | t
 btree  | can_multi_col | t
 btree  | can_exclude   | t

正如我们所看到的，B-树可以对数据进行排序并支持唯一性——这是唯一一种为我们提供类似属性的访问方法。也允许使用多列索引，但其他访问方法（尽管不是所有方法）也可能支持此类索引。我们下次将讨论排除约束的支持（这是有原因的）。

     name      | pg_index_has_property
---------------+-----------------------
 clusterable   | t
 index_scan    | t
 bitmap_scan   | t
 backward_scan | t

“btree”访问方法支持两种获取值的技术：索引扫描和位图扫描。正如我们所见，访问方法可以“向前”和“向后”遍历树。

        name        | pg_index_column_has_property 
--------------------+------------------------------
 asc                | t
 desc               | f
 nulls_first        | f
 nulls_last         | t
 orderable          | t
 distance_orderable | f
 returnable         | t
 search_array       | t
 search_nulls       | t

该层的前四个属性解释了特定列的值是如何精确排序的。在本例中，值按升序（“asc”）排序，空值放在最后（“NULLs_last”）。但正如我们已经看到的，其他组合是可能的。

“search_array”属性表示索引支持这样的表达式：

demo=# explain(costs off)
select * from aircrafts where aircraft_code in ('733','763','773');

                           QUERY PLAN                            
-----------------------------------------------------------------
 Index Scan using aircrafts_pkey on aircrafts
   Index Cond: (aircraft_code = ANY ('{733,763,773}'::bpchar[]))
(2 rows)

“returnable”属性表示支持仅索引扫描，这是合理的，因为索引行本身存储索引值（与哈希索引不同）。在这里，讲几句关于基于B-树覆盖索引（仅索引扫描）的话是有意义的。

具有附加行的唯一索引

正如我们前面讨论的，覆盖索引是存储查询所需的所有值的索引，（几乎）不需要访问表本身。一个独特的索引可以专门覆盖（所需的字段数据）。

但是，假设我们想要将查询所需的额外列添加到唯一索引中（就是在索引中加一列，成为多列索引）。新复合键的值现在可能不唯一，因此需要在同一列上使用两个索引：一个唯一（用于支持完整性约束），另一个非唯一（用作覆盖）。这肯定是低效的。

在我们公司，Anastasiya Lubennikova改进了“btree”方法，以便在唯一索引中包含其他非唯一列。我们希望，该补丁会被社区采用，成为PostgreSQL的一部分，但这不会早在版本10中出现。在这一点上，补丁在Pro标准9.5+版中可用，它看起来就是这样。

【事实上，这个补丁被提交到了PG11里】

让我们考虑订购表：

demo=# \d bookings

              Table "bookings.bookings"
    Column    |           Type           | Modifiers
--------------+--------------------------+-----------
 book_ref     | character(6)             | not null
 book_date    | timestamp with time zone | not null
 total_amount | numeric(10,2)            | not null
Indexes:
    "bookings_pkey" PRIMARY KEY, btree (book_ref)
Referenced by:
    TABLE "tickets" CONSTRAINT "tickets_book_ref_fkey" FOREIGN KEY (book_ref) 
REFERENCES bookings(book_ref)

在该表中，主键（book_ref，预订码）由常规的“btree”索引提供。让我们用一个附加列创建一个新的唯一索引：

demo=# create unique index bookings_pkey2 on bookings(book_ref) 
       INCLUDE (book_date);

现在，我们用一个新索引替换现有索引（在事务中进行，以同时应用所有更改）：

demo=# begin;

demo=# alter table bookings drop constraint bookings_pkey cascade;

demo=# alter table bookings add primary key using index bookings_pkey2;

demo=# alter table tickets add foreign key (book_ref) references bookings (book_ref);

demo=# commit;

我们得到如下结果：

demo=# \d bookings

              Table "bookings.bookings"
    Column    |           Type           | Modifiers
--------------+--------------------------+-----------
 book_ref     | character(6)             | not null
 book_date    | timestamp with time zone | not null
 total_amount | numeric(10,2)            | not null
Indexes:
    "bookings_pkey2" PRIMARY KEY, btree (book_ref) INCLUDE (book_date)
Referenced by:
    TABLE "tickets" CONSTRAINT "tickets_book_ref_fkey" FOREIGN KEY (book_ref) 
REFERENCES bookings(book_ref)

现在，同一个索引作为唯一索引工作，并用作此查询的覆盖索引，例如：

demo=# explain(costs off)
select book_ref, book_date from bookings where book_ref = '059FC4';

                    QUERY PLAN                    
--------------------------------------------------
 Index Only Scan using bookings_pkey2 on bookings
   Index Cond: (book_ref = '059FC4'::bpchar)
(2 rows)

索引创建

众所周知且重要的是，对于大型表，最好在不使用索引的情况下加载数据，然后创建所需的索引。这不仅更快，而且很可能索引的大小也更小。

因为创建“btree”索引的过程比在树中按行插入值更高效。大致上，表中所有可用的数据都会被排序，并创建这些数据的叶页。然后，内部页面“构建”在这个基础上，直到整个金字塔收敛到根。

此过程的速度取决于可用RAM的大小，而可用RAM的大小受“maintenance_work_mem”参数的限制。因此，增加参数值可以加快过程。对于唯一索引，除了“maintenance_work_mem”之外，还会分配大小为“work_mem”的内存。

比较（运算符）语义

上一次我们提到PostgreSQL需要知道调用哪些哈希函数来针对不同数据类型，并且这种关联存储在“哈希”访问方法中。同样，系统必须弄清楚如何对值进行排序。这对于排序、分组（有时）、归并连接等都是必需的。PostgreSQL不会将它绑定到运算符名称（例如>，<，=），因为用户可以定义自己的数据类型，并为相应的运算符指定不同的名称。“btree”访问方法使用的运算符族定义了运算符名称。

例如，这些比较运算符在“bool_ops”运算符族中使用：

postgres=# select   amop.amopopr::regoperator as opfamily_operator,
         amop.amopstrategy
from     pg_am am,
         pg_opfamily opf,
         pg_amop amop
where    opf.opfmethod = am.oid
and      amop.amopfamily = opf.oid
and      am.amname = 'btree'
and      opf.opfname = 'bool_ops'
order by amopstrategy;


  opfamily_operator  | amopstrategy
---------------------+-------------- 
 <(boolean,boolean)  |            1
 <=(boolean,boolean) |            2
 =(boolean,boolean)  |            3
 >=(boolean,boolean) |            4
 >(boolean,boolean)  |            5
(5 rows) 

这里我们可以看到五个比较运算符，但正如前面提到的，我们不应该依赖它们的名称。为了弄清楚每个运营商会做哪些比较，引入了策略概念（有点像策略模式，就是对不同数据类型，执行类似的操作）。定义了五种策略来描述运算符语义：

• 1 — less
• 2 — less or equal
• 3 — equal
• 4 — greater or equal
• 5 — greater

一些操作符族可以包含多个运算符（运算符包括了参数类型，不同参数类型的运算符是不同的运算符），以实现一种策略。例如，“integer_ops”运算符族为策略1包含以下运算符：

postgres=# select   amop.amopopr::regoperator as opfamily_operator
from     pg_am am,
         pg_opfamily opf,
         pg_amop amop
where    opf.opfmethod = am.oid
and      amop.amopfamily = opf.oid
and      am.amname = 'btree'
and      opf.opfname = 'integer_ops'
and      amop.amopstrategy = 1
order by opfamily_operator;

  opfamily_operator  
---------------------- 
 <(integer,bigint)
 <(smallint,smallint)
 <(integer,integer)
 <(bigint,bigint)
 <(bigint,integer)
 <(smallint,integer)
 <(integer,smallint)
 <(smallint,bigint)
 <(bigint,smallint)
(9 rows) 

由于这一点，在比较一个操作符族中包含的不同类型的值时，优化器可以避免类型转换。

对新数据类型的索引支持

该文档提供了一个为复数创建新数据类型的示例，以及一个运算符类来对这种类型的值进行排序的示例。本例使用C语言，当速度非常关键时，这是绝对合理的。但是，为了更好地理解比较语义，没有什么能阻止我们使用纯SQL进行相同的实验。

让我们用两个字段创建一个新的复合类型：实部和虚部。

postgres=# create type complex as (re float, im float);

我们可以使用新类型的字段创建一个表，并向表中添加一些值：

postgres=# create table numbers(x complex);

postgres=# insert into numbers values ((0.0, 10.0)), ((1.0, 3.0)), ((1.0, 1.0));

现在出现了一个问题：如果没有数学意义上的顺序关系，如何对复数进行排序？ 事实证明，我们已经定义了比较运算符：

postgres=# select * from numbers order by x;

   x    
--------
 (0,10)
 (1,1)
 (1,3)
(3 rows)

默认情况下，对于复合类型，排序是按组件进行的：首先比较第一个字段，然后比较第二个字段，依此类推，大致与逐个字符比较文本字符串的方式相同。但我们可以定义不同的顺序。例如，复数可以被视为向量，并按模数（长度）排序，模数（长度）为坐标平方和的平方根（毕达哥拉斯定理）。为了定义这样的顺序，让我们创建一个计算模数的辅助函数：

postgres=# create function modulus(a complex) returns float as $$
    select sqrt(a.re*a.re + a.im*a.im);
$$ immutable language sql;

现在，我们将使用这个辅助函数为所有五个比较运算符系统地定义函数：

postgres=# create function complex_lt(a complex, b complex) returns boolean as $$
    select modulus(a) < modulus(b);
$$ immutable language sql;

postgres=# create function complex_le(a complex, b complex) returns boolean as $$
    select modulus(a) <= modulus(b);
$$ immutable language sql;

postgres=# create function complex_eq(a complex, b complex) returns boolean as $$
    select modulus(a) = modulus(b);
$$ immutable language sql;

postgres=# create function complex_ge(a complex, b complex) returns boolean as $$
    select modulus(a) >= modulus(b);
$$ immutable language sql;

postgres=# create function complex_gt(a complex, b complex) returns boolean as $$
    select modulus(a) > modulus(b);
$$ immutable language sql;

我们将创建相应的运算符。为了说明它们不需要被称为“>”、“<”等等，让我们给它们起个“奇怪”的名字。

postgres=# create operator #<#(leftarg=complex, rightarg=complex, procedure=complex_lt);

postgres=# create operator #<=#(leftarg=complex, rightarg=complex, procedure=complex_le);

postgres=# create operator #=#(leftarg=complex, rightarg=complex, procedure=complex_eq);

postgres=# create operator #>=#(leftarg=complex, rightarg=complex, procedure=complex_ge);

postgres=# create operator #>#(leftarg=complex, rightarg=complex, procedure=complex_gt);

至此，我们可以比较数字：

postgres=# select (1.0,1.0)::complex #<# (1.0,3.0)::complex;

 ?column?
----------
 t
(1 row)

除了五个运算符之外，“btree”访问方法还需要定义一个函数（过度但方便）：如果第一个值小于、等于或大于第二个值，则必须返回-1、0或1。这个辅助功能叫做“支持”。其他访问方法可能需要定义其他支持功能。

postgres=# create function complex_cmp(a complex, b complex) returns integer as $$
    select case when modulus(a) < modulus(b) then -1
                when modulus(a) > modulus(b) then 1 
                else 0
           end;
$$ language sql;

现在我们准备创建一个操作符类（将自动创建同名操作符族）：

postgres=# create operator class complex_ops
default for type complex
using btree as
    operator 1 #<#,
    operator 2 #<=#,
    operator 3 #=#,
    operator 4 #>=#,
    operator 5 #>#,
    function 1 complex_cmp(complex,complex);

现在，排序可以根据需要工作：

postgres=# select * from numbers order by x;

   x    
--------
 (1,1)
 (1,3)
 (0,10)
(3 rows)

它肯定会得到“btree”索引的支持。 要完成此图，您可以使用以下查询获取支持函数：

postgres=# select amp.amprocnum,
       amp.amproc,
       amp.amproclefttype::regtype,
       amp.amprocrighttype::regtype
from   pg_opfamily opf,
       pg_am am,
       pg_amproc amp
where  opf.opfname = 'complex_ops'
and    opf.opfmethod = am.oid
and    am.amname = 'btree'
and    amp.amprocfamily = opf.oid;

 amprocnum |   amproc    | amproclefttype | amprocrighttype
-----------+-------------+----------------+-----------------
         1 | complex_cmp | complex        | complex
(1 row)

内部

我们可以使用“pageinspect”扩展来探索B树的内部结构。

demo=# create extension pageinspect;

索引元页面：

demo=# select * from bt_metap('ticket_flights_pkey');

 magic  | version | root | level | fastroot | fastlevel
--------+---------+------+-------+----------+-----------
 340322 |       2 |  164 |     2 |      164 |         2
(1 row)

这里最有趣的是索引级别：对于一个有一百万行的表，两列上的索引只需要两个级别（不包括根）。

164块（根）的统计信息：

demo=# select type, live_items, dead_items, avg_item_size, 
       page_size, free_size
from bt_page_stats('ticket_flights_pkey',164);

type | live_items | dead_items | avg_item_size | page_size | free_size
------+------------+------------+---------------+-----------+-----------
 r    |         33 |          0 |            31 |      8192 |      6984
(1 row)

以及块中的数据（“数据”字段包含二进制表示的索引键的值，此处由于屏幕宽度截取显示）：

demo=# select itemoffset, ctid, itemlen, left(data,56) as data
from bt_page_items('ticket_flights_pkey',164) limit 5;

 itemoffset |  ctid   | itemlen |                           data                           
------------+---------+---------+----------------------------------------------------------
          1 | (3,1)   |       8 |
          2 | (163,1) |      32 | 1d 30 30 30 35 34 33 32 33 30 35 37 37 31 00 00 ff 5f 00
          3 | (323,1) |      32 | 1d 30 30 30 35 34 33 32 34 32 33 36 36 32 00 00 4f 78 00
          4 | (482,1) |      32 | 1d 30 30 30 35 34 33 32 35 33 30 38 39 33 00 00 4d 1e 00
          5 | (641,1) |      32 | 1d 30 30 30 35 34 33 32 36 35 35 37 38 35 00 00 2b 09 00
(5 rows)

第一个元素与技术有关，并指定块中所有元素的上限（我们没有讨论实现细节），而数据本身从第二个元素开始。很明显，最左边的子节点是块163，然后是块323，依此类推。反过来，可以使用相同的函数来探索它们。

现在，遵循一个好的传统，阅读文档、自述文件和源代码是有意义的。

然而，还有一个潜在的有用扩展是“amcheck”，它将被合并到PostgreSQL 10中，对于较低版本，您可以从github获得它。这种扩展检查B树中数据的逻辑一致性，使我们能够提前检测故障。

【事实确实如此，从版本10开始，“amcheck”是PostgreSQL的一部分】