LeetCode算法练习——动态规划提高（四）

LeetCode139. 单词拆分

给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict，判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。

示例 1：

输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以被拆分成 "leet code"。

示例 2：

输入: s = "applepenapple", wordDict = ["apple", "pen"]
输出: true
解释: 返回 true 因为 "applepenapple" 可以被拆分成 "apple pen apple"。
     注意你可以重复使用字典中的单词。

示例 3：

输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
输出: false

• 1. 定义：dp[i]表示s的前i个字符能否拆分成一个或多个wordDict字典中的单词 所以需要定义dp的长度为s.size() + 1；
• 2. dp[0] = true 表示空字串是可以拆分成字典中的单词 即：前0个字符是可以拆分成字典中的单词；
• 3. 状态转移方程: dp[i] = dp[j] && s[j, i - 1] dp[j]表示s[0, j - 1]和s[j, i - 1]是否同时在字典中；
• 4. s = "leetcode", wordDict = ["leet", "code"]，dp[8] = dp[4] + check("code") (1)dp[4] = true 表示s[0, 3] = "leet"是字典中的单词 (2) check("code") 即s[4,7] 表示检查"code"是不是字典中的单词。

class Solution {
public:
    bool wordBreak(string s, vector& wordDict) {
        unordered_set set;
        for(string str : wordDict) set.insert(str);
        int length = s.size();
        vector dp(length + 1, false);
        dp[0] = true;
        for(int i = 1; i < length + 1; i++){
            for(int j = 0; j < i; j++){
                if(dp[j] && set.find(s.substr(j, i - j)) != set.end()){//集合中找寻子串
                    dp[i] = true;
                    break;
                }
            }
        }
        return dp[length];
    }
};

LeetCode152. 乘积最大子数组

给你一个整数数组 nums ，请你找出数组中乘积最大的连续子数组（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。

示例 1:

输入: [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。

示例 2:

输入: [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。

此题思路是用贪心算法，实际可以归类于是一种动态规划问题，由于存在负数，我们需要记录当前最大值和当前最小值。每次遍历用先前的最值乘以当前值，更新最值和最大乘积。

class Solution {
public:
    int maxProduct(vector& nums) {
        int len = nums.size(), res = nums[0];
        int prevMin = nums[0], prevMax = nums[0];
        int nagtive = 0, postive = 0;
        for (int i = 1; i < len; i++) {
            nagtive = prevMin * nums[i];                      //最小负值*当前值
            postive = prevMax * nums[i];                      //最大正值*当前值
            prevMin = min(min(nagtive, postive), nums[i]);    //当前最小值
            prevMax = max(max(nagtive, postive), nums[i]);    //当前最大值
            res = max(prevMax, res);
        }
        return res;
    }
};

LeetCode377. 组合总和 Ⅳ

给定一个由正整数组成且不存在重复数字的数组，找出和为给定目标正整数的组合的个数。

示例:

nums = [1, 2, 3]
target = 4

所有可能的组合为：
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)

请注意，顺序不同的序列被视作不同的组合。

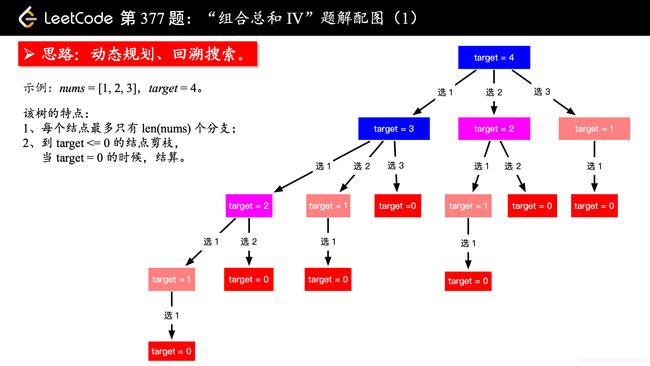
因此输出为 7。

 此题有点类似与LeetCode518零钱兑换2的思路，不同点在于，元素出现顺序不同也是一种组合，思路如下：

状态

对于“状态”，我们首先思考能不能就用问题当中问的方式定义状态，上面递归树都画出来了。当然就用问题问的方式。dp[i] ：对于给定的由正整数组成且不存在重复数字的数组，和为 i 的组合的个数。思考输出什么？因为状态就是问题当中问的方式而定义的，因此输出就是最后一个状态 dp[n]。

状态转移方程

由上面的树形图，可以很容易地写出状态转移方程：

dp[i] = sum{dp[i - num] for num in nums and if i >= num}

注意：在 0 这一点，我们定义 dp[0] = 1 的，它表示如果 nums 里有一个数恰好等于 target，它单独成为 1 种可能。

class Solution {
public:
    int combinationSum4(vector& nums, int target) {
        vector dp(target + 1, 0);
        dp[0] = 1;
        for(int i = 1; i <= target; i++){
            for(int j = 0; j < nums.size(); j++){
                if(i - nums[j] >= 0)
                    dp[i] += dp[i - nums[j]];
                else continue;
            }
        }
        return dp[target];
    }
};