【论文笔记】Graph WaveNet for Deep Spatial-Temporal Graph Modeling
Graph WaveNet for Deep Spatial-Temporal Graph Modeling
摘要
现有模型大多是基于固定的图结构，但由于数据的损失可能导致某些true dependency丢失。现有方法对捕获时间趋势不是很有效，因为RNN和CNN不能捕获长时间序列。
GWN是通过更新一个自适应依赖矩阵，从而来捕获隐藏的空间依赖。GWN使用堆叠的1D卷积分结构，来使接受域不断扩大，从而使得模型可以处理非常长的序列。
介绍
假设1：一个结点的未来信息取决于一个结点的历史信息与相邻结点的历史信息。
问题1：图中结点间相互信息可能出现缺失或增加。
问题2：目前的时空建模难以学习到时间依赖。RNN容易出现梯度爆炸/消失，CNN需要很多1D卷积层（接受域随层数线性增长）。
GWN是基于CNN的，图卷积层中具有自适应调整矩阵，可通过端到端学习，从而保障矩阵保存隐藏的时间依赖。在WaveNet的启发下，采用了堆叠扩展随机卷积来捕获时间依赖性，随着层数堆叠，接受域线性增长，从而可以接受长范围时间序列。
方法
该模型实现采用了GCN和TCN，他们一同组成了网络，从而捕获时空依赖。
采用0-1矩阵表示结点连接，不同的时刻对应拥有不同的特征矩阵（图信号）。
图卷积层
图卷积可以提取结点结构特征信息，该模型中将切比雪夫谱滤波器作为了一个组合层，通过整合和转换来平滑结点信号：
Z = A ~ X W Z=\tilde{A}XW Z=A~XW
Li等人提出了扩散卷积层（diffusion convolution layer），该层被证明对时空建模有效。将上式推广可得：
Z = ∑ k = 0 K P k X W k Z=\sum^{K}_{k=0}P^kXW_k Z=k=0∑KPkXWk
其中 P k P^k Pk表示变换矩阵的幂数级，在无向图中， P = A / r o w s u m ( A ) P=A/rowsum(A) P=A/rowsum(A)；在有向图中，传播过程分为两个方向，正向变换矩阵为 P f = A / r o w s u m ( A ) P_f=A/rowsum(A) Pf=A/rowsum(A)，反向变换矩阵为 P b = A T / r o w s u m ( A T ) P_b=A^T/rowsum(A^T) Pb=AT/rowsum(AT)，在考虑两个方向的情况下，该公式为：
Z = ∑ k = 0 K P f k X W k 1 + P b k X W k 2 Z=\sum^{K}_{k=0}P^{k}_{f}XW_{k1}+P^{k}_{b}XW_{k2} Z=k=0∑KPfkXWk1+PbkXWk2
自适应邻接矩阵
自适应邻接矩阵 A ~ a d p \tilde{A}_{adp} A~adp不需要任何先验知识，其在梯度下降过程中进行端到端学习，从而发现隐藏的空间依赖。
实现该策略的方法是用可学习的参数 E 1 , E 2 E_1,E_2 E1,E2随机初始化两个结点嵌入，则自适应邻接矩阵可以被定义为：
A ~ a d p = S o f t M a x ( R e L U ( E 1 E 2 T ) ) \tilde{A}_{adp}=SoftMax(ReLU(E_1E_2^T)) A~adp=SoftMax(ReLU(E1E2T))
根据该矩阵，我们可以获得源结点和目标结点间的空间依赖权重。根据结合预定义的空间依赖和自学习的隐藏图依赖，故有图卷积层：
Z = ∑ k = 0 K P f k K W k 1 + P b k K W k 2 + A ~ a p t k K W k 3 Z=\sum^{K}_{k=0}P^k_fKW_{k1}+P^k_bKW_{k2}+\tilde{A}^{k}_{apt}KW_{k3} Z=k=0∑KPfkKWk1+PbkKWk2+A~aptkKWk3
当图结构不可获得时，可以仅用自适应邻接矩阵来获取隐藏空间依赖，即：
Z = ∑ k = 0 K A ~ a p t k X W k Z=\sum^K_{k=0}\tilde{A}^k_{apt}XW_k Z=k=0∑KA~aptkXWk
时间卷积层（TCN）
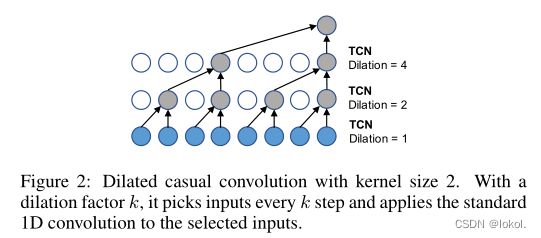
该模型中使用了dilated causal convolution作为TCN层，采用它，相比于RNN可以有效处理长范围序列，并且进行并行计算并有效减少梯度爆炸问题。
同时，该层可以通过填充0来保持空间因果关系，从而使得对当前时刻的预测仅涉及历史信息。
在给定1D输入序列 x ∈ R T x\in R^T x∈RT及核 F ∈ R K F\in R^K F∈RK的情况下，该层在时刻 t t t的操作可以表示为：
x ⋆ f ( t ) = ∑ s = 0 K − 1 f ( s ) x ( t − d × s ) x\star f(t)=\sum^{K-1}_{s=0}f(s)x(t-d\times s) x⋆f(t)=s=0∑K−1f(s)x(t−d×s)
其中， d d d是膨胀系数，用于控制跳过距离。
有效节约计算资源。
门TCN
门机制（gating mechanisms）在RNN中很重要，能有效控制信息流在时间卷积网络中的层间流动。
h = g ( θ 1 ⋆ χ + b ) ⨀ σ ( θ ⋆ χ + c ) h=g(\theta_1\star \chi +b)\bigodot\sigma(\theta\star \chi +c) h=g(θ1⋆χ+b)⨀σ(θ⋆χ+c)
χ ∈ R N × D × S \chi \in R^{N\times D\times S} χ∈RN×D×S是输入， ⨀ \bigodot ⨀是矩阵对应同位置相乘， g ( ⋅ ) g(·) g(⋅)是激活函数用于决定信息传递到下一层的概率。模型中采用了门TCN来学习复杂时间依赖。模型采用了正切双曲函数作为激活函数。
GWN结构
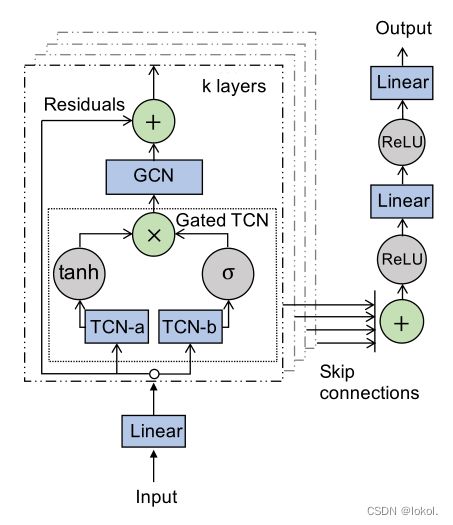
GWN结构中，由 K K K个时空层组成和一个输出层。输入首先被一个线形层转换，然后依次经过门TCN以及GCN。每一层时空层都有循环连接并且与输出层相连。
GWN结构中，存在两个平行的TCN层（TCN-a，TCN-b）。GCN输入是 [ N , C , L ] [N,C,L] [N,C,L]，其中 N N N是结点数， C C C是隐藏维度， L L L是序列长度，将图卷积应用于 h [ : , : , i ] ∈ R N × C h[:,:,i]\in R^{N\times C} h[:,:,i]∈RN×C。使用MAR作为loss。
模型输出为连续预测序列 X ^ ( t + 1 ) + ( t + T ) \hat{X}^{(t+1)+(t+T)} X^(t+1)+(t+T)，为实现连续序列，人为设计了GWN的接受域大小等于输入，从而使得在最后一个时空层中输出的时间维数恰好等于1。
实验
使用的数据集为METR-LA以及PEMS-BAY。其中METR-LA包含洛杉矶高速公路上207个传感器记录了四个月的车速数据。PEMS-BAY包含海湾地区325个传感器记录的六个月的车速数据。邻接矩阵中的结点使用阈值高斯核被道路交通网络的距离构建，Z-score归一化被用于输入。
实验步骤
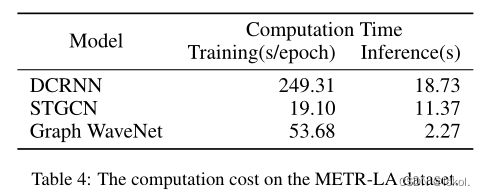
在7系i9X CPU和Titan Xp GPU上进行实验。
- 实验中使用了8层GWN，膨胀系数分别是1，2，1，2，1，2，1，2。
- 使用无自适应矩阵的图卷积层，diffusion step K = 2 K=2 K=2。
- 使用均匀分布随机初始化了size为10的节点嵌入。
- 使用的优化器是Adam，初始学习率0.001。
- 使用的Dropout p是0.3，被用在了图卷积层的输出。
- 评价用的是MAE、RMSE、MAPE。
- 在训练和测试中都包含丢失值。
实验结果
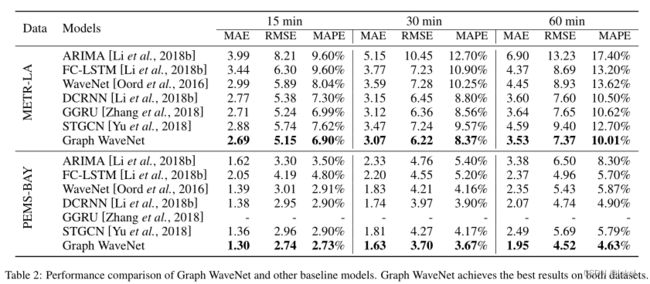
实验中比较了15min、30min、60min情况下GWN和baseline在METR-LA和PEMS-BAY数据集。
采用自适应邻接矩阵
为证明自适应邻接矩阵的有效性，GWN使用了5种不同的配置。Adaptive-only的表现好于Forward-only的表现。Forward-backward-adaptvie模型所拥有的分数最低，模型最优。
从a图与对应的b图中可以看到，第9行存在的高值点多于47行，在地图上对应的是第9行交叉路口更多。
训练时间
GWN是最具性价比的。这是因为GWN在一次运行中就生成12个预测，二其他必须根据之前的预测生成结果。