简单认识红黑树
文章目录
- 前言
- 一、树
- 二、二叉树
-
- 二叉树简介
- 遍历二叉树
- 三、红黑树
-
- 红黑树简介
- 红黑树的自我调整
前言
上面两篇文章简单的讲解了ArrayList和LinkedList，他们的底层结构使用的是数组与链表，比较简单。下面要讲解HashMap，由于使用的为JDK8，HashMap采用了数组+链表+红黑树的底层结构了，可能有部分人对红黑树不太了解，本文就先对红黑树进行下说明。
一、树
树是一种数据结构，它是由n(n≥0)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：
每个节点有零个或多个子节点；没有父节点的节点称为根节点；每一个非根节点有且只有一个父节点；除了根节点外，每个子节点可以分为多个不相交的子树。
我们常见的组织部门、家族族谱等就是树状结构的。
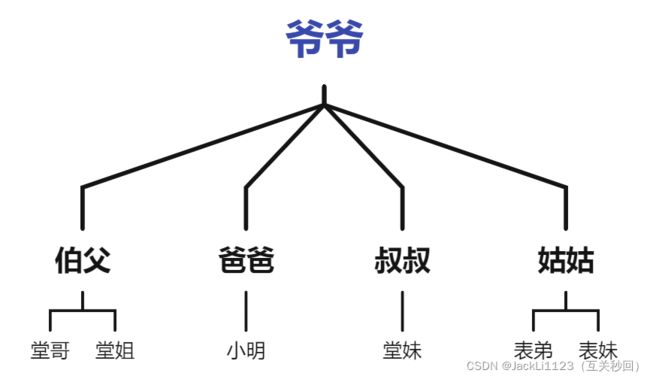
树是由n（n≥0）个节点构成的有限集合：
- 当n=0没有节点时被称为空树；当n>0时的树被称为非空树。
- 非空树中每个元素都被称为节点(Node)；
- 所有节点中仅有一个节点被称为根节点(Root Node)；
- 其余的节点分为m个互不相交的有限集合，每个集合又是一个树，称为根的子树；
- 其余的节点根据其位置又分为中间节点(有子节点的节点)和叶子节点(没有子节点的节点)；
在上面的图中的树是三层的树，爷爷属于根节点，第二代属于中间节点，第三代属于叶子节点；
二、二叉树
二叉树简介
二叉树是一种特殊的树，二叉树的每个节点最多有两个子节点，其中左边的节点称为左子节点(left child)，右边的节点被称为右子节点(right child)。
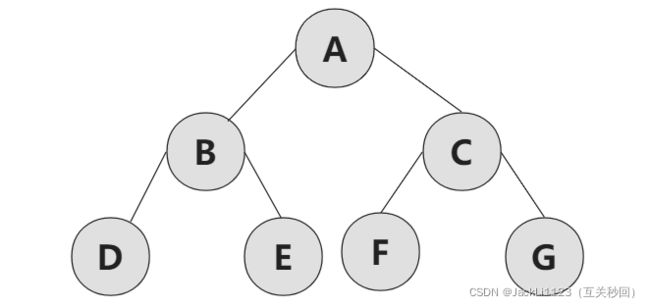
如图就是个二叉树，由于二叉树子节点最多两个，我们就可以知道二叉树的节点个数与 2n 有关，所以二叉树的第i层上至多有2（i-1）个节点；深度为h的二叉树中至多含有2h-1个节点。
简单的写个二叉树的代码实现：
public class BinaryTree {
private Node root;
/**
* 插入节点的递归操作
* @param node
* @param data
* @return
*/
private Node insert(Node node, int data) {
if (node == null) { //插入到最底层了直接创建返回
return new Node(data);
}
//递归插入，一直到最底层
if (data < node.data) {//小于插在左边
node.leftChild = insert(node.leftChild, data);
} else if (data > node.data) {//大于插在右边
node.rightChild = insert(node.rightChild, data);
}
return node;
}
/**
* 插入节点
* @param data
*/
public void insertNode(int data) {
root = insert(root, data);
}
/**
* 节点类
*/
class Node {
int data;
Node leftChild;
Node rightChild;
Node(int data) {
this.data = data;
}
}
}
写个测试类：
public static void main(String[] args) {
BinaryTree binaryTree = new BinaryTree();
binaryTree.insertNode(10);
binaryTree.insertNode(8);
binaryTree.insertNode(11);
binaryTree.insertNode(7);
binaryTree.insertNode(9);
binaryTree.insertNode(12);
}
最终执行结果形成的树是这样的
遍历二叉树
数组和链表等线性结构我们都遍历过，二叉树同样也可以遍历，二叉树的遍历是沿着某条线路进行遍历的，当线路确定后数据按照线路来看就编程了线性结构了。二叉树根据其遍历的路线可以分为：
- 前序遍历： 前序遍历的顺序先访问根节点，再访问左节点，最后访问右节点。前序遍历表现出来的是向左的斜线顺序，按照从左到右的斜线顺序来的，如图：10->8->7这是一条线，9自己是一条，12->11是一条线，13自己是一条线，所以前序遍历的结果是10->8->7->9->12->11->13。
看一下前序遍历的代码实现：
public void preOrder(Node node) {
if (node == null) {
return;
}
System.out.println(node.data);
preOrder(node.leftChild);
preOrder(node.rightChild);
}
- 中序遍历： 中序遍历的顺序先访问左节点，再访问根节点，最后访问右节点。中序遍历其实跟上面一样，但是它是反着来的，7->8,然后9 ，此时左节点遍历完了，遍历根节点10，再右节点11->12,然后13，最终结果：7->8->9->10->11->12->13。
//
public void inOrder(Node node) {
if (node == null) {
return;
}
inOrder(node.leftChild);
System.out.println(node.data);
inOrder(node.rightChild);
}
- 后序遍历： 后序遍历的顺序先访问左节点，再访问右节点，最后访问根节点。后序遍历可以看做是是从下往上，从左到右的层序遍历，但是这个层是断的，左层序遍历和右层序遍历，最后为根节点。上面最终的结果为7->9->8->11->13->12->10。
//因为它的打印放在了后面，所以是倒着打印的
public void postOrder(Node node) {
if (node == null) {
return;
}
postOrder(node.leftChild);
postOrder(node.rightChild);
System.out.println(node.data);
}
- 层序遍历： 层序遍历的顺序先访问根节点，然后一层层的往下遍历，每层从左往右遍历。例如上面的10,8->12,7->9->11->13。最终的顺序为10->8->12->7->9->11->13。
public void levelOrder(Node root) { //通过队列来实现，因为队列是先入先出的
Queue<Node> queue = new LinkedList<Node>();
queue.offer(root);
while (!queue.isEmpty()) { //每次循环从左往右放入节点
Node node = queue.poll();
System.out.println(node.data);
if (node.leftChild != null) { //左节点放进去
queue.offer(node.leftChild);
}
if (node.rightChild != null) { //又节点放进去
queue.offer(node.rightChild);
}
}
}
三、红黑树
红黑树简介
二叉树查找确实方便了，但是其还是有个缺点的，假设我们放的一直是左子节点，例如我们放的顺序是5、4、3、2、1。最终结果会变成这样，变成了个线性结构。
所以我们需要二叉树有自我调节能力，让二叉树一直保持着根节点为中间位置的值，左右保持着平衡状态，这就衍生出了平衡二叉树也就是红黑树。
红黑树有下面特点：
- 每个节点要么是黑色，要么是红色。
- 根节点是黑色的。
- 每个叶子节点都是黑色的空结点，大多数情况下省略说明，记得最外面都是空节点就行。
- 如果一个节点是红色的，则它的子节点必须是黑色的，父子不能都是红色，但是可以都是黑色，新插入的节点默认是红色的。
- 从任一结点到其每个叶子的所有路径都所包含黑色节点的数量是一样的。
红黑树的规则这么严格，假设我们删除或者新增了一个节点，那就不符合规则了，这个时候红黑树需要自我调整让其再次符合规则，调节过程分为：左旋、右旋和颜色反转三种方式。
节点代码：
//出于代码演示方便就不写private类型的了
public class RBNode {
int key; //存放的值假设int类型的
int color; //颜色 假设1代表红色 0代表黑色
RBNode left; //左子节点
RBNode right; //右子节点
RBNode parent; //父节点
static final int RED = 1;
static final int BLACK = 0;
public RBNode(int key) {
this.key = key;
this.color = RED; //新节点为红色
}
}
红黑树代码：
public class RBTree {
RBNode root; //根节点
...内部方法在下面需要借助图片进行讲解，不写在里面了
}
红黑树的自我调整
- 左旋： 左旋指的是红黑树右边的节点比较多了，这时候红黑树的重心是偏右的，我们尽量保持着红黑树的重心在中间，所以需要根节点下来去左边，然后将右节点推上去作为根节点。
左旋示例代码，没有考虑比较庞大的树，正常代码要比这个复杂的多：
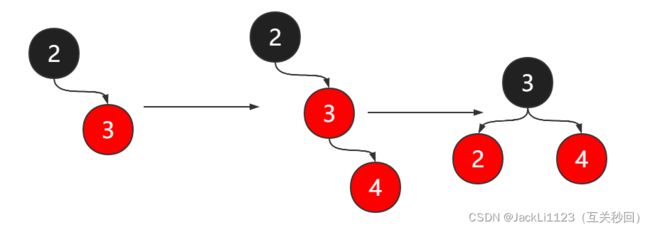
//假设上图，存在节点2和3，插入节点2，对3进行左旋
private void leftRotate(RBNode node){
//记录下父节点2来
RBNode parent = node.parent;
//将节点2下降为节点3的左子节点
node.left = parent;
//将节点3设置为节点2的父节点
parent.parent = node;
}
- 右旋： 右旋是跟左旋相反的，指的是红黑树左边的节点比较多了，这时候红黑树的重心是偏左的，我们尽量保持着红黑树的重心在中间，所以需要根节点下来去右边，然后将左节点推上去作为根节点。
//存在节点4和3，插入节点2，对节点3进行右旋
private void rightRotate(RBNode node){
//记录节点3的父节点4
RBNode parent = node.parent;
//将节点4下降为节点3的右子节点
node.right = parent;
//将节点4的父节点设置为节点3
parent.parent = node;
}
- 颜色反转： 我们调整了红黑树的结构了可能会出现父子节点同时红色的情况，我们就需要将子节点上面的节点的颜色反转过来，让其达到不同时为红色的结果。
//传递节点1上面的翻转，不考虑继续向上递归颜色翻转了，只是简单的实例说明
private void flipColors(RBNode node){
//节点1的祖辈节点3
RBNode grandfather = node.parent.parent;
//设置父辈为黑色
node.parent.color = RBNode.BLACK;
//判断祖辈是不是根节点，不是修改为红色
if(root.key == grandfather.key){
grandfather.color = RBNode.BLACK;
}else{
grandfather.color = RBNode.RED;
}
//设置叔伯辈为黑色
grandfather.left.color = RBNode.BLACK;
grandfather.right.color = RBNode.BLACK;
}
下面来演示个插入节点后红黑树自我调整的场景，假设有个树存在4和2两个节点。
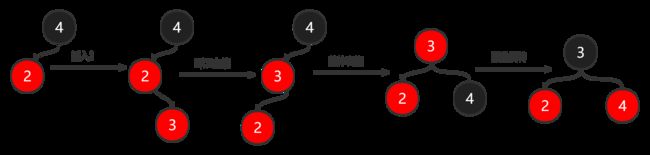
红黑树的插入分为五种情况：
- 新插入的节点为根节点，新插入的节点是红色的，但是因为规则2的限制这个时候直接把新节点设置为黑色。
- 新插入节点的父节点是黑色节点，这时候直接插入新的节点就行，如果不是根节点，不需要考虑规则2，只需要考虑规则4、5就行，父子节点不同色，规则4满足，插入了红色节点不影响路径上黑色节点的数量，所以规则5也满足。
- 新插入节点的父节点是红色的，并且是父节点的右子节点，还是上面的演示图，不满足规则4，如果直接右旋顺序是不满足的，需要先对新节点2和父节点3做左旋，让新节点2变成父节点3，此时父子节点(2和3)还是同色的，如果我们直接将3改为黑色则不满足规则5了，所以需要再进行一次右旋，然后翻转颜色，此时节点3到下面节点的黑色节点的数量是相同的。
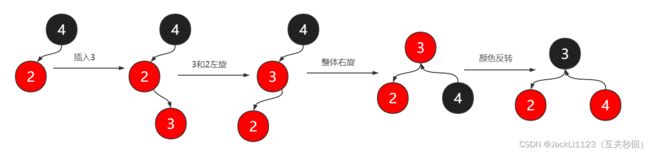
- 新插入节点的父节点是黑色的，并且是父节点的左节点，如下图所示，这时候可以直接右旋，这是满足节点顺序的，但是不满足规则4，父子节点同色了，所以需要颜色翻转，将节点2修改为黑色，同时节点2到子节点的黑色节点数量要保持一致，所以节点4修改为了红色。
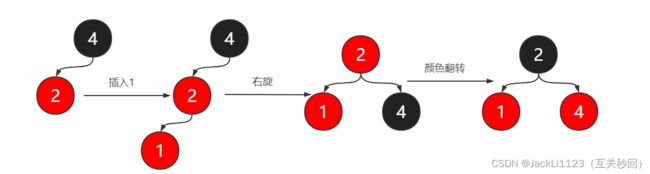
- 新插入节点的父节点包括叔伯辈的节点也是红色的，如下图所示，插入节点1，父子节点同色了，此时需要将上面的节点进行颜色翻转，颜色翻转完成后如果祖父辈的节点是根节点为了满足规则2需要将其修改为黑色。
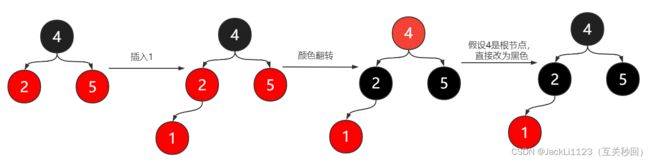
新插入节点基本分为上面5中情况，其实并不需要完全按照上面的逻辑思路来走，只要记住红黑树的五条规则，让其满足这五条规则就行了。
后面补上插入规则的示例代码。