关于“labuladong的算法小抄”的学习笔记---第0章核心框架汇总的后半部分技巧（c++版）

前言

【由于算法小抄大部分代码都是java，而作者其实是学c++的，因此，本笔记在记录的同时，对作者的java代码进行了转换，希望也能够帮到大家】这是第0章的后半部分（因为怕文章太长自己都不好找，正好前半部分讲的框架，后半部分讲的是技巧)–需要前半部分的请点击此处。

一、回溯算法秒杀所有排列/组合/子集问题

无论是排列、组合还是子集问题，简单说无非就是让你从序列 nums 中以给定规则取若干元素，主要有以下几种变体：
形式一、元素无重不可复选，即 nums 中的元素都是唯一的，每个元素最多只能被使用一次，这也是最基本的形式。以组合为例，如果输入 nums = [2,3,6,7]，和为 7 的组合应该只有 [7]。
形式二、元素可重不可复选，即 nums 中的元素可以存在重复，每个元素最多只能被使用一次。以组合为例，如果输入 nums = [2,5,2,1,2]，和为 7 的组合应该有两种 [2,2,2,1] 和 [5,2]。
形式三、元素无重可复选，即 nums 中的元素都是唯一的，每个元素可以被使用若干次。以组合为例，如果输入 nums = [2,3,6,7]，和为 7 的组合应该有两种 [2,2,3] 和 [7]。（可重可复选没啥意思，都属于形式三）
上面用组合问题举的例子，但排列、组合、子集问题都可以有这三种基本形式，所以共有 9 种变化。除此之外，题目也可以再添加各种限制条件，比如让你求和为 target 且元素个数为 k 的组合，那这么一来又可以衍生出一堆变体，怪不得面试笔试中经常考到排列组合这种基本题型。
但无论形式怎么变化，其本质就是穷举所有解，而这些解呈现树形结构，所以合理使用回溯算法框架，稍改代码框架即可把这些问题一网打尽。
记住这两种树形结构就能解决所有相关问题：


首先，组合问题和子集问题其实是等价的，这个后面会讲；至于之前说的三种变化形式，无非是在这两棵树上剪掉或者增加一些树枝罢了。

回溯和DFS之间区别—遍历树枝or遍历节点

// DFS 算法，关注点在节点
void traverse(TreeNode* root) {
    if (root == nullptr) return;
    printf("进入节点 %s", root);
    for (TreeNode* child : root->children) {
        traverse(child);
    }
    printf("离开节点 %s", root);
}

// 回溯算法，关注点在树枝
void backtrack(TreeNode* root) {
    if (root == nullptr) return;
    for (TreeNode* child : root->children) {
        // 做选择
        printf("从 %s 到 %s", root, child);
        backtrack(child);
        // 撤销选择
        printf("从 %s 到 %s", child, root);
    }
}

因此，我们也可以通过这个区别来分别选择关注【树枝】还是关注【节点】，其实最大的区别就是根节点会不会遗漏。

1、子集（元素无重不可复选）

【题目】力扣第 78 题「 子集」就是这个问题：
题目给你输入一个无重复元素的数组 nums，其中每个元素最多使用一次，请你返回 nums 的所有子集。
首先，我们通过保证元素之间的相对顺序不变来防止出现重复的子集。因此结果就跟上上个图是一样的了。注意这棵树的特性：
如果把根节点作为第 0 层，将每个节点和根节点之间树枝上的元素作为该节点的值，那么第 n 层的所有节点就是大小为 n 的所有子集。比如大小为 2 的子集就是这一层节点的值：

PS：注意，本文之后所说「节点的值」都是指节点和根节点之间树枝上的元素，且将根节点认为是第 0 层。

想计算所有子集，那只要遍历这棵多叉树，把所有节点的值收集起来不就行了？因此直接看代码

vector<vector<int>> res;
// 记录回溯算法的递归路径
vector<int> track;

// 主函数
public vector<vector<int>> subsets(vector<int> nums) {
    backtrack(nums, 0);
    return res;
}

// 回溯算法核心函数，遍历子集问题的回溯树
void backtrack(vector<int> nums, int start) {

    // 前序位置，每个节点的值都是一个子集
    res.push_back(track);
    
    // 回溯算法标准框架
    for (int i = start; i < nums.length; i++) {
        // 做选择
        track.push_back(nums[i]);
        // 通过 start 参数控制树枝的遍历，避免产生重复的子集
        backtrack(nums, i + 1);
        // 撤销选择
        track.pop_back();
    }
}

我们使用 start 参数控制树枝的生长避免产生重复的子集，用 track 记录根节点到每个节点的路径的值，同时在前序位置把每个节点的路径值收集起来，完成回溯树的遍历就收集了所有子集。最后，backtrack 函数开头看似没有 base case，会不会进入无限递归？
其实不会的，当 start == nums.length 时，叶子节点的值会被装入 res，但 for 循环不会执行，也就结束了递归。

2、组合（元素无重不可复选）

如果你能够成功的生成所有无重子集，那么你稍微改改代码就能生成所有无重组合了。
组合和子集是一样的：大小为 k 的组合就是大小为 k 的子集。
【题目】比如力扣第 77 题「 组合」：
给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。
以 nums = [1,2,3] 为例，刚才让你求所有子集，就是把所有节点的值都收集起来；现在你只需要把第 2 层（根节点视为第 0 层）的节点收集起来，就是大小为 2 的所有组合：

反映到代码上，只需要稍改 base case，控制算法仅仅收集第 k 层节点的值即可：

vector<vector<int>> res;
// 记录回溯算法的递归路径
vector<int> track;

// 主函数
public vector<vector<int>>combine(int num, int k) {
    backtrack(num, 0, k);
    return res;
}

// 回溯算法核心函数，遍历子集问题的回溯树
void backtrack(vector<int> nums, int start, int k) {

// base case
    if (k == track.size()) {
        // 遍历到了第 k 层，收集当前节点的值
        res.push_back(track);
        return;
    }
    // 回溯算法标准框架
    for (int i = start; i < nums; i++) {
        // 做选择
        track.push_back(i);
        // 通过 start 参数控制树枝的遍历，避免产生重复的子集
        backtrack(num, i + 1, k);
        // 撤销选择
        track.pop_back();
    }
}

这样，标准的子集问题也解决了。

3、排列（元素无重不可复选）

排列问题在前文回溯算法核心框架讲过，这里就简单过一下。
【题目】力扣第 46 题「 全排列」就是标准的排列问题：
给定一个不含重复数字的数组 nums，返回其所有可能的全排列
刚才讲的组合/子集问题使用 start 变量保证元素 nums[start] 之后只会出现 nums[start+1…] 中的元素，通过固定元素的相对位置保证不出现重复的子集。但排列问题本身就是让你穷举元素的位置，nums[i] 之后也可以出现 nums[i] 左边的元素，所以之前的那一套玩不转了，需**要额外使用 used 数组来标记哪些元素还可以被选择。**标准全排列可以抽象成如下这棵二叉树：

vector<vector<int>> res;

/* 主函数，输入一组不重复的数字，返回它们的全排列 */
vector<vector<int>> permute(vector<int> nums) {
    // 记录「路径」
    vector<int> track;
    // 「路径」中的元素会被标记为 true，避免重复使用
    int n = nums.size();
    vector<bool> used(n);
    backtrack(nums, track, used);
    return res;
}

// 回溯算法核心函数
void backtrack(vector<int> nums, vector<int> track, vector<bool> used) {
    // base case，到达叶子节点
    if (track.size() == nums.size()) {
    // 收集叶子节点上的值
        res.push_back(track);
        return;
    }
    
    for (int i = 0; i < nums.size(); ++i) {
          // 已经存在 track 中的元素，不能重复选择
        if (used[i]) {
            // nums[i] 已经在 track 中，跳过
            continue;
        }
        // 做选择
        track.push_back(nums[i]);
        used[i] = true;
        // 进入下一层决策树
        backtrack(nums, track, used);
        // 取消选择
        track.pop_back();
        used[i] = false;
    }
}

但如果题目不让你算全排列，而是让你算元素个数为 k 的排列，怎么算？
也很简单，改下 backtrack 函数的 base case，仅收集第 k 层的节点值即可：

// 回溯算法核心函数
void backtrack(vector<int> nums, vector<int> track, vector<bool> used,int k) {
    // base case，到达第 k 层，收集节点的值
    if (track.size() == k) {
        // 第 k 层节点的值就是大小为 k 的排列
        res.push_back(track);
        return;
    }
    // 回溯算法标准框架
    for (int i = 0; i < nums.length; i++) {
        // ...
        backtrack(nums, track, used, k);
        // ...
    }
}

4、子集/组合（元素可重不可复选）

【题目】力扣第 90 题「 子集 II」就是这样一个问题：
给你一个整数数组 nums，其中可能包含重复元素，请你返回该数组所有可能的子集。
按照之前的思路画出子集的树形结构，显然，两条值相同的相邻树枝会产生重复：

所以我们需要进行剪枝，如果一个节点有多条值相同的树枝相邻，则只遍历第一条，剩下的都剪掉，不要去遍历：

体现在代码上，需要先进行排序，让相同的元素靠在一起，如果发现 nums[i] == nums[i-1]，则跳过：

vector<vector<int>> res;
vector<int> track;

public vector<vector<int>>> subsetsWithDup(vector<int> nums) {
    // 先排序，让相同的元素靠在一起
    sort(nums.begin(),nums.end());
    backtrack(nums, 0);
    return res;
}
void backtrack(vector<int> nums, int start) {
    // 前序位置，每个节点的值都是一个子集
    res.push_back(track);

    for (int i = start; i < nums.size(); ++i) 
    {
        // 剪枝逻辑，值相同的相邻树枝，只遍历第一条
        if (i > start && nums[i] == nums[i - 1]) 
        {
            continue;
        }
        track.push_back(nums[i]);
        backtrack(nums, i + 1);
        track.pop_back();
    }
}

这段代码和之前标准的子集问题的代码几乎相同，就是添加了排序和剪枝的逻辑。
组合问题和子集问题是等价的
【题目】力扣第 40 题「 组合总和 II」：
给你输入 candidates 和一个目标和 target，从 candidates 中找出中所有和为 target 的组合。candidates 可能存在重复元素，且其中的每个数字最多只能使用一次。
对比子集问题的解法，只要额外用一个 trackSum 变量记录回溯路径上的元素和，然后将 base case 改一改即可解决这道题：

vector<vector<int>> res;
vector<int> track;
// 记录 track 中的元素之和
int trackSum = 0;
public vector<vector<int>>> combinationSum2(vector<int> nums, int target) {
	if (candidates.size() == 0) 
		{
	        return res;
    	}
    // 先排序，让相同的元素靠在一起
    sort(nums.begin(),nums.end());
    backtrack(nums, 0, target);
    return res;
}
// 回溯算法主函数
void backtrack(vector<int> nums, int start, int target) {
    // base case，达到目标和，找到符合条件的组合
    if(trackSum == target){
    	res.push_back(track);
    	return;
    	}
    // base case，超过目标和，直接结束
    if (trackSum > target) {
        return;
    }
    for (int i = start; i < nums.size(); ++i) 
    {
        // 剪枝逻辑，值相同的相邻树枝，只遍历第一条
        if (i > start && nums[i] == nums[i - 1]) 
        {
            continue;
        }
        track.push_back(nums[i]);
        trackSum += nums[i];
        backtrack(nums, i + 1, target);
        track.pop_back();
         trackSum -= nums[i];
    }
}

5、排列（元素可重不可复选）

【题目】我们看看力扣第 47 题「 全排列 II」，给你输入一个可包含重复数字的序列 nums，请你写一个算法，返回所有可能的全排列。
先看解法代码：

vector<vector<int>> res;
vector<int> track;
vector<bool> uesd；

public vector<vector<int>> permuteUnique(vector<int> nums) {
    // 先排序，让相同的元素靠在一起
    sort(nums.begin(),nums.end());
    used.resize(nums.size());
    backtrack(nums);
    return res;
}

void backtrack(int[] nums) {
    if (track.size() == nums.size()) {
        res.push_back(track);
        return;
    }

    for (int i = 0; i < nums.length; i++) {
        if (used[i]) {
            continue;
        }
        // 新添加的剪枝逻辑，固定相同的元素在排列中的相对位置
        if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
            continue;
        }
        track.push_back(nums[i]);
        used[i] = true;
        backtrack(nums);
        track.pop_back();
        used[i] = false;
    }
}

对比一下之前的标准全排列解法代码，这段解法代码只有两处不同：
1、对 nums 进行了排序。
2、添加了一句额外的剪枝逻辑。
注意排列问题的剪枝逻辑，和子集/组合问题的剪枝逻辑略有不同：新增了 !used[i - 1] 的逻辑判断。
正常来说，机器对于[1,2,2’] 和 [1,2’,2] 应该只被算作同一个排列，但被算作了两个不同的排列。因此需要保证相同元素在排列中的相对位置保持不变。
比如说 nums = [1,2,2’] 这个例子，我保持排列中 2 一直在 2’ 前面。
这样的话，你从上面 6 个排列中只能挑出 3 个排列符合这个条件：

[ [1,2,2'],[2,1,2'],[2,2',1] ]

这就是正确的答案了
进一步，如果 nums = [1,2,2’,2’‘]，我只要保证重复元素 2 的相对位置固定，比如说 2 -> 2’ -> 2’'，也可以得到无重复的全排列结果。
标准全排列算法之所以出现重复，是因为把相同元素形成的排列序列视为不同的序列，但实际上它们应该是相同的；而如果固定相同元素形成的序列顺序，当然就避免了重复。，反映在代码上就是

// 新添加的剪枝逻辑，固定相同的元素在排列中的相对位置
if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
    // 如果前面的相邻相等元素没有用过，则跳过
    continue;
}
// 选择 nums[i]

当出现重复元素时，比如输入 nums = [1,2,2’,2’‘]，2’ 只有在 2 已经被使用的情况下才会被选择，同理，2’’ 只有在 2’ 已经被使用的情况下才会被选择，这就保证了相同元素在排列中的相对位置保证固定。

这里拓展一下，如果你把上述剪枝逻辑中的 !used[i - 1] 改成 used[i - 1]，其实也可以通过所有测试用例，但效率会有所下降，这是为什么呢？因为这个写法剪掉的树枝不够多。之所以这样修改不会产生错误，是因为这种写法相当于维护了 2’’ -> 2’ -> 2 的相对顺序，最终也可以实现去重的效果。

6、子集/组合（元素无重可复选）

【题目】直接看力扣第 39 题「 组合总和」：给你一个无重复元素的整数数组 candidates 和一个目标和 target，找出 candidates 中可以使数字和为目标数 target 的所有组合。candidates 中的每个数字可以无限制重复被选取。
想解决这种类型的问题，也得回到回溯树上，我们不妨先思考思考，**标准的子集/组合问题是如何保证不重复使用元素的？**答案在于 backtrack 递归时输入的参数 start。这个 i 从 start 开始，那么下一层回溯树就是从 start + 1 开始，从而保证 nums[start] 这个元素不会被重复使用

// 无重组合的回溯算法框架
void backtrack(vector<int> nums, int start) {
    for (int i = start; i < nums.size(); i++) {
        // ...
        // 递归遍历下一层回溯树，注意参数
        backtrack(nums, i + 1);
        // ...
    }
}

那么反过来，如果我想让每个元素被重复使用，我只要把 i + 1 改成 i 即可.这相当于给之前的回溯树添加了一条树枝，在遍历这棵树的过程中，一个元素可以被无限次使用。
当然，这样这棵回溯树会永远生长下去，所以我们的递归函数需要设置合适的 base case 以结束算法，即路径和大于 target 时就没必要再遍历下去了。

vector<vector<int>> res;
vector<int> track;
// 记录 track 中的元素之和
int trackSum = 0;
public vector<vector<int>>> combinationSum(vector<int> candidates, int target) {
	if (candidates.size() == 0) 
		{
	        return res;
    	}
    // 先排序，让相同的元素靠在一起
    backtrack(nums, 0, target);
    return res;
}
// 回溯算法主函数
void backtrack(vector<int> nums, int start, int target) {
    // base case，达到目标和，找到符合条件的组合
    if(trackSum == target){
    	res.push_back(track);
    	return;
    	}
    // base case，超过目标和，直接结束
    if (trackSum > target) {
        return;
    }
     // 回溯算法标准框架
    for (int i = start; i < nums.size(); ++i) 
    {
   		 // 选择 nums[i]
        track.push_back(nums[i]);
        trackSum += nums[i];
        // 递归遍历下一层回溯树
        // 同一元素可重复使用，注意参数
        backtrack(nums, i, target);// 此处的i+1改成i就ok
        // 撤销选择 nums[i]
         track.pop_back();
         trackSum -= nums[i];
    }
}

7、排列（元素无重可复选）

力扣上没有类似的题目，我们不妨先想一下，nums 数组中的元素无重复且可复选的情况下，会有哪些排列？
比如输入 nums = [1,2,3]，那么这种条件下的全排列共有 3^3 = 27 种：

[
  [1,1,1],[1,1,2],[1,1,3],[1,2,1],[1,2,2],[1,2,3],[1,3,1],[1,3,2],[1,3,3],
  [2,1,1],[2,1,2],[2,1,3],[2,2,1],[2,2,2],[2,2,3],[2,3,1],[2,3,2],[2,3,3],
  [3,1,1],[3,1,2],[3,1,3],[3,2,1],[3,2,2],[3,2,3],[3,3,1],[3,3,2],[3,3,3]
]

标准的全排列算法利用 used 数组进行剪枝，避免重复使用同一个元素。如果允许重复使用元素的话，直接放飞自我，去除所有 used 数组的剪枝逻辑就行了。

vector<vector<int>> res;
/* 主函数，输入一组不重复的数字，返回它们的全排列 */
vector<vector<int>> permute(vector<int> nums) {
    // 记录「路径」
    vector<int> track;
    // 「路径」中的元素会被标记为 true，避免重复使用
    int n = nums.size();
    backtrack(nums, track);
    return res;
}

// 回溯算法核心函数
void backtrack(vector<int> nums, vector<int> track) {
    // base case，到达叶子节点
    if (track.size() == nums.size()) {
    // 收集叶子节点上的值
        res.push_back(track);
        return;
    }
    
    for (int i = 0; i < nums.size(); ++i) {
        // 做选择
        track.push_back(nums[i]);
        // 进入下一层决策树
        backtrack(nums, track);
        // 取消选择
        track.pop_back();
    }
}

!!!最后总结—排列/组合/子集问题的三种形式的代码!!!

前言：注意，1、其组合/子集和排列的大区别就是《组合/子集在for循环内i是从start开始，这样不会回头，而排列是从0开是的，其可以回头，从而出现不同的顺序！
2、其次在排序中used是是为了不让用过的元素继续用的，因此里面存放的是i序号，而不是元素值，为什么是序号呢，因为排序中每次循环i又会从0开始！
3、子集是没有固定的退出条件的，它循环完了就自己退出了，不用人工设置！

1、元素无重不可复选

即 nums 中的元素都是唯一的，每个元素最多只能被使用一次，backtrack 核心代码如下：

/* 组合/子集问题回溯算法框架 */
void backtrack(vector<int> nums, int start) {
    // 回溯算法标准框架
    for (int i = start; i < nums.size(); ++i) {
        // 做选择
        track.push_back(nums[i]);
        // 注意参数
        backtrack(nums, i + 1);
        // 撤销选择
        track.pop_back();
    }
}
--------------------------------------------
/* 排列问题回溯算法框架 */
void backtrack(vector<int> nums) {
    for (int i = 0; i < nums.length; i++) {
        // 剪枝逻辑
        if (used[i]) {
            continue;
        }
        // 做选择
        used[i] = true;
        track.push_back(nums[i]);
        backtrack(nums);
        // 撤销选择
        track.pop_back();
        used[i] = false;
    }
}

2、元素可重不可复选

即 nums 中的元素可以存在重复，每个元素最多只能被使用一次，其关键在于排序和剪枝，backtrack 核心代码如下：

sort(nums.begin(),nums.end());
/* 组合/子集问题回溯算法框架 */
void backtrack(vector<int> nums, int start) {
    // 回溯算法标准框架
    for (int i = start; i < nums.size(); i++) {
        // 剪枝逻辑，跳过值相同的相邻树枝
        // 注意这里的i>start包括排序方法中i>0都是为了num【i-1】的边界条件而生的
        if (i > start && nums[i] == nums[i - 1]) {
            continue;
        }
        // 做选择
        track.push_back(nums[i]);
        // 注意参数
        backtrack(nums, i + 1);
        // 撤销选择
        track.pop_back();
    }
}

------------------------------------------
sort(nums.begin(),nums.end());
/* 排列问题回溯算法框架 */
void backtrack(vector<int> nums) {
    for (int i = 0; i < nums.size(); ++i) {
        // 剪枝逻辑
        if (used[i]) {
            continue;
        }
        // 剪枝逻辑，固定相同的元素在排列中的相对位置
        if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
            continue;
        }
        // 做选择
        used[i] = true;
        track.push_back(nums[i]);
        backtrack(nums);
        // 撤销选择
        track.pop_back();
        used[i] = false;
    }
}

3、元素不可重可复选/可重可复选

即 nums 中的元素都是唯一的，每个元素可以被使用若干次，只要删掉去重逻辑即可，backtrack 核心代码如下：

/* 组合/子集问题回溯算法框架 */
void backtrack(int[] nums, int start) {
    // 回溯算法标准框架
    for (int i = start; i < nums.length; i++) {
        // 做选择
        track.push_back(nums[i]);
        // 注意参数!!!!!
        backtrack(nums, i);
        // 撤销选择
        track.pop_back();
    }
}
-------------------------------------------------
/* 排列问题回溯算法框架 */
void backtrack(vector<int> nums) {
    for (int i = 0; i < nums.size(); ++i) {
        // 做选择
        track.push_back(nums[i]);
        backtrack(nums);
        // 撤销选择
        track.pop_back();
    }
}

二、双指针技巧秒杀七道链表题目

对于单链表相关的题目，双指针的运用是非常广泛的。

1、合并两个有序链表

这题比较简单，我们直接看解法：

ListNode mergeTwoLists(ListNode* l1, ListNode* l2) {
    // 虚拟头结点
    ListNode* dummy = new ListNode(-1), p = dummy;
    ListNode* p1 = l1, p2 = l2;
    
    while (p1 != nullptr && p2 != nullptr) {
        // 比较 p1 和 p2 两个指针
        // 将值较小的的节点接到 p 指针
        if (p1->val > p2->val) {
            p->next = p2;
            p2 = p2->next;
        } else {
            p->next = p1;
            p1 = p1->next;
        }
        // p 指针不断前进
        p = p->next;
    }
    
    if (p1 != nullptr) {
        p->next = p1;
    }
    
    if (p2 != nullptr) {
        p->next = p2;
    }
    return dummy->next;
}

这个算法的逻辑类似于「拉拉链」，l1, l2 类似于拉链两侧的锯齿，指针 p 就好像拉链的拉索，将两个有序链表合并。
代码中还用到一个链表的算法题中是很常见的「虚拟头结点」技巧，也就是 dummy节点。你可以试试，如果不使用dummy 虚拟节点，代码会复杂很多，而有了dummy节点这个占位符，可以避免处理空指针的情况，降低代码的复杂性。

2、合并 k 个有序链表(面试常考题)

合并 k 个有序链表的逻辑类似合并两个有序链表，难点在于，如何快速得到 k 个节点中的最小节点，接到结果链表上？
这里我们就要用到 优先级队列（二叉堆） 这种数据结构，把链表节点放入一个最小堆，就可以每次获得 k 个节点中的最小节点：

class Solution {
public:
    struct Status {
        int val;
        ListNode *ptr;
        bool operator < (const Status &rhs) const {
            return val > rhs.val;//这是最小堆，因为默认最大堆嘛，所以靠修改<
        }
    };
	 // 优先级队列，最小堆
    priority_queue <Status> pq;
    ListNode* mergeKLists(vector<ListNode*>& lists) {
    ListNode* dummy = new ListNode(-1), p = dummy;
    // 将 k 个链表的头结点加入最小堆
        for (auto node: lists) {
            if (node) pq.push({node->val, node});
        }
        while (!pq.empty()) {
         // 获取最小节点，接到结果链表中
            auto f = pq.top(); 
            pq.pop();
            p->next = f.ptr;
            //如果当前最小的节点还有下一个节点，就继续放进去 
            if (f.ptr->next) q.push({f.ptr->next->val, f.ptr->next});
            // p 指针不断前进
            p = p->next;
        }
        return dummy->next;
    }
};

优先队列 pq 中的元素个数最多是 k，所以一次 pop 或者 push方法的时间复杂度是 O(logk)；所有的链表节点都会被加入和弹出 pq，所以算法整体的时间复杂度是 O(Nlogk)，其中 k 是链表的条数，N 是这些链表的节点总数。

3、 单链表的倒数第 k 个节点

是算法题一般只给你一个 ListNode 头结点代表一条单链表，你不能直接得出这条链表的长度 n，而需要先遍历一遍链表算出 n 的值，然后再遍历链表计算第 n - k + 1 个节点。这样是两次遍历。
我们能不能只遍历一次链表，就算出倒数第 k 个节点？可以做到的，如果是面试问到这道题，面试官肯定也是希望你给出只需遍历一次链表的解法（其实就是空间换时间）。即找到n-k：
1、我们先让一个指针 p1 指向链表的头节点 head，然后走 k 步，而在的 p1，只要再走 n - k 步，就能走到链表末尾的空指针了。
2、趁这个时候，再用一个指针 p2 指向链表头节点 head，让 p1 和 p2 同时向前走，p1 走到链表末尾的空指针时前进了 n - k 步，p2 也从 head 开始前进了 n - k 步，停留在第 n - k + 1 个节点上，即恰好停链表的倒数第 k 个节点上。

// 返回链表的倒数第 k 个节点
ListNode* findFromEnd(ListNode* head, int k) {
    ListNode* p1 = head;
    // p1 先走 k 步
    for (int i = 0; i < k; ++i) {
        p1 = p1->next;
    }
    ListNode* p2 = head;
    // p1 和 p2 同时走 n - k 步
    while (p1 != nullptr) {
        p2 = p2->next;
        p1 = p1->next;
    }
    // p2 现在指向第 n - k 个节点
    return p2;
}

很多链表相关的算法题都会用到这个技巧，比如说力扣第 19 题「 删除链表的倒数第 N 个结点」：

ListNode* findFromEnd(ListNode* head, int k) {
    // 代码见上文
}
// 主函数
ListNode* removeNthFromEnd(ListNode* head, int n) {
    // 虚拟头结点
    ListNode dummy = new ListNode(-1);
    dummy->next = head;
    // 删除倒数第 n 个，要先找倒数第 n + 1 个节点
    ListNode* x = findFromEnd(dummy, n + 1);
    // 删掉倒数第 n 个节点
    x->next = x->next->next;
    return dummy->next;
}

4、单链表的中点

力扣第 876 题「 链表的中间结点」就是这个题目，问题的关键也在于我们无法直接得到单链表的长度 n，常规方法也是先遍历链表计算 n，再遍历一次得到第 n / 2 个节点，也就是中间节点。
如果想一次遍历就得到中间节点，也需要耍点小聪明，使用「快慢指针」的技巧：
每当慢指针 slow 前进一步，快指针 fast 就前进两步，这样，当 fast 走到链表末尾时，slow 就指向了链表中点。

ListNode* middleNode(ListNode* head) {
    // 快慢指针初始化指向 head
    ListNode* slow = head, fast = head;
    // 快指针走到末尾时停止
    while (fast != nullptr && fast->next != nullptr) {
        // 慢指针走一步，快指针走两步
        slow = slow->next;
        fast = fast->next->next;
    }
    // 慢指针指向中点
    return slow;
}

需要注意的是，如果链表长度为偶数，也就是说中点有两个的时候，我们这个解法返回的节点是靠后的那个节点。

5、判断链表是否包含环

判断链表是否包含环属于经典问题了，解决方案也是用快慢指针：
如果 fast 最终遇到空指针，说明链表中没有环；如果 fast 最终和 slow 相遇，那肯定是 fast 超过了 slow 一圈，说明链表中含有环。
当然，这个问题还有进阶版：如果链表中含有环，如何计算这个环的起点？
这个题，我在我前面的博客《力扣数据结构基础刷题总结》中的链表部分的第一节总结过，因此就不po原理了（其中有地方（第一圈必被逮到）特别有意思），这里就直接看一下code了

ListNode* detectCycle(ListNode* head) {
    ListNode* fast, slow;
    fast = slow = head;
    while (fast != nullptr && fast.next != nullptr) {
        fast = fast->next->next;
        slow = slow->next;
        if (fast == slow) break;
    }
    // 上面的代码类似 hasCycle 函数
    if (fast == nullptr || fast->next == nullptr) {
        // fast 遇到空指针说明没有环
        return nullptr;
    }

    // 重新指向头结点
    slow = head;
    // 快指针也变成慢指针，与新的慢指针同步前进，相交点就是环起点
    while (slow != fast) {
        fast = fast->next;
        slow = slow->next;
    }
    return slow;
}

6、两个链表是否相交

这个题，我在我前面的博客《力扣数据结构基础刷题总结》中的链表部分的第二节总结过，因此就不仔细解释原理了，这里就直接看一下code了
解决这个问题的关键是，通过某些方式，让 p1 和 p2 能够同时到达相交节点 c1。所以，我们可以让 p1 遍历完链表 A 之后开始遍历链表 B，让 p2 遍历完链表 B 之后开始遍历链表 A，这样相当于「逻辑上」两条链表接在了一起。

ListNode* getIntersectionNode(ListNode* headA, ListNode* headB) {
    // p1 指向 A 链表头结点，p2 指向 B 链表头结点
    ListNode* p1 = headA, p2 = headB;
    while (p1 != p2) {
        // p1 走一步，如果走到 A 链表末尾，转到 B 链表
        if (p1 == nullptr) p1 = headB;
        else            p1 = p1->next;
        // p2 走一步，如果走到 B 链表末尾，转到 A 链表
        if (p2 == nullptr) p2 = headA;
        else            p2 = p2->next;
    }
    return p1;
}

这样，这道题就解决了，空间复杂度为 O(1)，时间复杂度为 O(N)。

三、我写了首诗，把二分搜索算法变成了默写题

二分查找并不简单，Knuth 大佬（发明 KMP 算法的那位）都说二分查找：思路很简单，细节是魔鬼。很多人喜欢拿整型溢出的 bug 说事儿，但是二分查找真正的坑根本就不是那个细节问题，而是在于到底要给 mid 加一还是减一，while 里到底用 <= 还是 <。

！！！二分查找框架！！！

int binarySearch(vector<int> nums, int target) {
    int left = 0, right = ...;
    while(...) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            ...
        } else if (nums[mid] < target) {
            left = ...
        } else if (nums[mid] > target) {
            right = ...
        }
    }
    return ...;
}

分析二分查找的一个技巧是：不要出现 else，而是把所有情况用 else if 写清楚，这样可以清楚地展现所有细节。
PS:计算 mid 时需要防止溢出，代码中 left + (right - left) / 2 就和 (left + right) / 2 的结果相同，但是有效防止了 left 和 right 太大，直接相加导致溢出的情况。

1、寻找一个数（基本的二分搜索）

这个场景是最简单的，可能也是大家最熟悉的，即搜索一个数，如果存在，返回其索引，否则返回 -1。

int binarySearch(vector<int> nums, int target) {
    int left = 0; 
    int right = nums.size() - 1; // 注意

    while(left <= right) {
        int mid = left + (right - left) / 2;
        if(nums[mid] == target)
            return mid; 
        else if (nums[mid] < target)
            left = mid + 1; // 注意
        else if (nums[mid] > target)
            right = mid - 1; // 注意
    }
    return -1;
}

下面用三个问题来讨论细节：
1、为什么 while 循环的条件中是 <=，而不是 <？【搜索区间】
这二者可能出现在不同功能的二分查找中，区别是：前者相当于两端都闭区间 [left, right]，后者相当于左闭右开区间 [left, right)，因为索引大小为 nums.size() 是越界的。
【如何分析？】
while(left <= right) 的终止条件是 left == right + 1，写成区间的形式就是 [right + 1, right]，或者带个具体的数字进去 [3, 2]，可见这时候区间为空，因为没有数字既大于等于 3 又小于等于 2 的吧。所以这时候 while 循环终止是正确的，直接返回 -1 即可。
而 while(left < right) 的终止条件是 left == right，写成区间的形式就是 [right, right]，或者带个具体的数字进去 [2, 2]，这时候区间非空，还有一个数 2，但此时 while 循环终止了。也就是说这区间 [2, 2] 被漏掉了，索引 2 没有被搜索，如果这时候直接返回 -1 就是错误的。
2、为什么 left = mid + 1，right = mid - 1？我看有的代码是 right = mid 或者 left = mid，没有这些加加减减，到底怎么回事，怎么判断？
刚才明确了「搜索区间」这个概念，而且本算法的搜索区间是两端都闭的，即 [left, right]。下一步应去搜索区间 [left, mid-1] 或者区间 [mid+1, right] 对不对？因为 mid 已经搜索过，应该从搜索区间中去除。
3、此算法有什么缺陷？
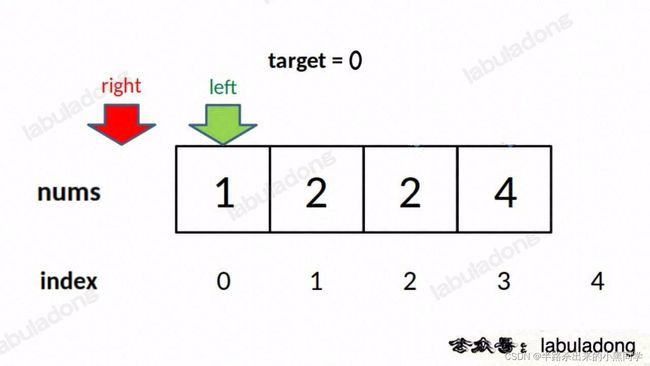
有序数组 nums = [1,2,2,2,3]，target 为 2，此算法返回的索引是 2，没错。但是如果我想得到 target 的左侧边界，即索引 1，或者我想得到 target 的右侧边界，即索引 3，这样的话此算法是无法处理的。
这样的需求很常见，你也许会说，找到一个 target，然后向左或向右线性搜索不行吗？可以，但是不好，因为这样难以保证二分查找对数级的复杂度了。

2、寻找左侧边界的二分搜索

[注意]当目标元素 target 不存在数组 nums 中时，搜索左侧边界的二分搜索的返回值可以做以下几种解读：
1、返回的这个值是 nums 中大于等于 target 的最小元素索引。
2、返回的这个值是 target 应该插入在 nums 中的索引位置。
3、返回的这个值是 nums 中小于 target 的元素个数。
比如在有序数组 nums = [2,3,5,7] 中搜索 target = 4，搜索左边界的二分算法会返回 2，你带入上面的说法，都是对的。

int left_bound(vector<int> nums, int target) {
    if (nums.size() == 0) return -1;
    int left = 0;
    int right = nums.size(); // 注意
    
    while (left < right) { // 注意
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            right = mid;
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid; // 注意
        }
    }
    return left;
}

下面用六个问题来讨论细节：
1、为什么 while 中是 < 而不是 <=?
答：用相同的方法分析，因为 right = nums.size() 而不是 nums.size() - 1。因此每次循环的「搜索区间」是 [left, right) 左闭右开。
while(left < right) 终止的条件是 left == right，此时搜索区间 [left, left) 为空，所以可以正确终止。

PS：这里先要说一个搜索左右边界和上面这个算法的一个区别，也是很多读者问的：刚才的 right 不是 nums.size() - 1 吗，为啥这里非要写成 nums.length 使得「搜索区间」变成左闭右开呢？

因为对于搜索左右侧边界的二分查找，这种写法比较普遍，我就拿这种写法举例了，保证你以后遇到这类代码可以理解。你非要用两端都闭的写法反而更简单，我会在后面写相关的代码，把三种二分搜索都用一种两端都闭的写法统一起来，你耐心往后看就行了。

2、为什么没有返回 -1 的操作？如果 nums 中不存在 target 这个值，怎么办？
答：函数的返回值（即 left 变量的值）取值区间是闭区间 [0, nums.size()]，所以我们简单添加两行代码就能在正确的时候 return -1：

// target 比所有数都大
if (left == nums.size()) return -1;
// 类似之前算法的处理方式
return nums[left] == target ? left : -1;//while(left < right) 的终止条件是 left == right，写成区间的形式就是 [right, right],此步就是为了防漏

3、为什么 left = mid + 1，right = mid ？和之前的算法不一样？
答：因为我们的「搜索区间」是 [left, right) 左闭右开，所以当 nums[mid] 被检测之后，下一步应该去 mid 的左侧或者右侧区间搜索，即 [left, mid) 或 [mid + 1, right)。
4、为什么该算法能够搜索左侧边界？
答：关键在于对于 nums[mid] == target 这种情况的处理,找到 target 时不要立即返回，而是缩小「搜索区间」的上界 right，在区间 [left, mid) 中继续搜索，即不断向左收缩，达到锁定左侧边界的目的。
5、为什么返回 left 而不是 right？
答：都是一样的，因为 while 终止的条件是 left == right。
6、能不能想办法把 right 变成 nums.size() - 1，也就是继续使用两边都闭的「搜索区间」？这样就可以和第一种二分搜索在某种程度上统一起来了。
答：当然可以，只要你明白了「搜索区间」这个概念，就能有效避免漏掉元素，随便你怎么改都行。
( right 应该初始化为 nums.size() - 1，while 的终止条件应该是 left == right + 1，也就是其中应该用 <=且因为搜索区间是两端都闭的，left 和 right 的逻辑需要更新)

int left_bound(vector<int> nums, int target) {
    int left = 0, right = nums.size() - 1;
    // 搜索区间为 [left, right]
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            // 搜索区间变为 [mid+1, right]
            left = mid + 1;
        } else if (nums[mid] > target) {
            // 搜索区间变为 [left, mid-1]
            right = mid - 1;
        } else if (nums[mid] == target) {
            // 收缩右侧边界
            right = mid - 1;
        }
    }
    // 检查出界情况---因为退出的时候left会比right大，因此若不存在小于target的元素，可能会超出去。
    if (left >= nums.size() || nums[left] != target) {
        return -1;
    }
    return left;
}

3、寻找右侧边界的二分查找

类似寻找左侧边界的算法，这里也会提供两种写法，还是先写常见的左闭右开的写法，只有两处和搜索左侧边界不同：

int right_bound(vector<int> nums, int target) {
    if (nums.size() == 0) return -1;
    int left = 0, right = nums.size();
    
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            left = mid + 1; // 注意
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid;
        }
    }
    return left - 1; // 注意
}

1、为什么这个算法能够找到右侧边界？
答：当 nums[mid] == target 时，不要立即返回，而是增大「搜索区间」的左边界 left，使得区间不断向右靠拢，达到锁定右侧边界的目的。
2、为什么最后返回 left - 1 而不像左侧边界的函数，返回 left？而且我觉得这里既然是搜索右侧边界，应该返回 right 才对。
答：首先，while 循环的终止条件是 left == right，所以 left 和 right 是一样的，你非要体现右侧的特点，返回 right - 1 好了。
至于为什么要减一，这是搜索右侧边界的一个特殊点，关键在锁定右边界时的这个条件判断：
因为我们对 left 的更新必须是 left = mid + 1，就是说 while 循环结束时，nums[left] 一定不等于 target 了，而 nums[left-1] 可能是 target。至于为什么 left 的更新必须是 left = mid + 1，当然是为了锁定右侧边界，就不再赘述。
3、为什么没有返回 -1 的操作？如果 nums 中不存在 target 这个值，怎么办？
答：
因为 while 的终止条件是 left == right，就是说 left 的取值范围是 [0, nums.size()]，所以可以添加两行代码，正确地返回 -1：

while (left < right) {
    // ...
}
if (left == 0) return -1;
return nums[left-1] == target ? (left-1) : -1;//while(left < right) 的终止条件是 left == right，写成区间的形式就是 [right, right],此步就是为了防漏

4、是否也可以把这个算法的「搜索区间」也统一成两端都闭的形式呢？这样这三个写法就完全统一了，以后就可以闭着眼睛写出来了。

int right_bound(vector<int> nums, int target) {
    int left = 0, right = nums.size() - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else if (nums[mid] == target) {
            // 这里改成收缩左侧边界即可
            left = mid + 1;
        }
    }
    // 这里改为检查 right 越界的情况，见下图
    if (right < 0 || nums[right] != target) {
        return -1;
    }
    return right;
}

越界的情况的具体分析过程同上面找左侧边界。

4、总结

接下来梳理一下这些细节差异的因果逻辑：
第一个，最基本的二分查找算法：

因为我们初始化 right = nums.size() - 1
所以决定了我们的「搜索区间」是 [left, right]
所以决定了 while (left <= right)
同时也决定了 left = mid+1 和 right = mid-1

因为我们只需找到一个 target 的索引即可
所以当 nums[mid] == target 时可以立即返回

第二个，寻找左侧边界的二分查找：

因为我们初始化 right = nums.size()
所以决定了我们的「搜索区间」是 [left, right)
所以决定了 while (left < right)
同时也决定了 left = mid + 1 和 right = mid

因为我们需找到 target 的最左侧索引
所以当 nums[mid] == target 时不要立即返回
而要收紧右侧边界以锁定左侧边界

第三个，寻找右侧边界的二分查找：

因为我们初始化 right = nums.size()
所以决定了我们的「搜索区间」是 [left, right)
所以决定了 while (left < right)
同时也决定了 left = mid + 1 和 right = mid

因为我们需找到 target 的最右侧索引
所以当 nums[mid] == target 时不要立即返回
而要收紧左侧边界以锁定右侧边界

又因为收紧左侧边界时必须 left = mid + 1
所以最后无论返回 left 还是 right，必须减一

对于寻找左右边界的二分搜索，常见的手法是使用左闭右开的「搜索区间」。但此处为了方便记忆，统一修改为两端都闭。

当目标元素不在nums里面时，明白左侧边界和右侧边界的二分搜索都指向什么！

【左侧】当目标元素 target 不存在数组 nums 中时，搜索左侧边界的二分搜索的返回值（返回left）可以做以下几种解读：
1、返回的这个值是 nums 中大于 target 的最小元素索引。
2、返回的这个值是 target 应该插入在 nums 中的索引位置。
3、返回的这个值是 nums 中小于 target 的元素个数。
比如在有序数组 nums = [2,3,5,7] 中搜索 target = 4，搜索左边界的二分算法会返回 2（也就是指向5），你带入上面的说法，都是对的。
而搜索右边界的二分算法就会返回1(也就是指向3)：
【右侧】因此，当目标元素 target 不存在数组 nums 中时，搜索右侧边界的二分搜索的返回值(返回right)，该值是nums 中小于 target 的最大元素索引。

！！！ 1、2、3节的默写秒杀二分搜索代码！！！

int binary_search(vector<int> nums, int target) {
    int left = 0, right = nums.size()- 1; 
    while(left <= right) {
        int mid = left + (right - left) / 2;//防止直接相加超类型
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1; 
        } else if(nums[mid] == target) {
            // 直接返回
            return mid;
        }
    }
    // 直接返回
    return -1;
}

int left_bound(vector<int> nums, int target) {
    int left = 0, right = nums.size()- 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else if (nums[mid] == target) {
            // 别返回，锁定左侧边界，收紧右侧
            right = mid - 1;
        }
    }
    // 最后要检查 left 越界的情况
    if (left >= nums.size()|| nums[left] != target) {
        return -1;
    }
    return left;
}

int right_bound(vector<int> nums, int target) {
    int left = 0, right = nums.size()- 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else if (nums[mid] == target) {
            // 别返回，锁定右侧边界，收紧左侧
            left = mid + 1;
        }
    }
    // 最后要检查 right 越界的情况
    if (right < 0 || nums[right] != target) {
        return -1;
    }
    return right;
}

四、我写了首诗，把滑动窗口算法变成了默写题

这个算法技巧的思路非常简单，就是维护一个窗口，不断滑动，然后更新答案么。LeetCode 上有起码 10 道运用滑动窗口算法的题目，难度都是中等和困难。该算法的大致逻辑如下：

int left = 0, right = 0;
while (right < s.size()) {
    // 增大窗口
    window.add(s[right]);
    ++right;
    
    while (window needs shrink) {
        // 缩小窗口
        window.remove(s[left]);
        left++;
    }
}

这个算法技巧的时间复杂度是 O(N)，比字符串暴力算法要高效得多。

！！！ 滑动窗口框架！！！

【提醒】 如果数组里面有负数，那么窗口的滑动就没有单向性了（没有负数的最大的优势是区间和具有“单调性”。单调性是一个非常好的性质，具有单调性的子数组相关问题可以很方便的使用二分查找、滑动窗口等方法解决），而此时对于这种情况，一个常用的处理方法是，考虑那些真正影响子数组能否满足题目条件或是否是最优解的“关键点”，着重维护这些关键点的信息。

套模板需要考虑四个问腿：
1、当移动 right 扩大窗口，即加入字符时，应该更新哪些数据？
2、什么条件下，窗口应该暂停扩大，开始移动 left 缩小窗口？
3、当移动 left 缩小窗口，即移出字符时，应该更新哪些数据？
4、我们要的结果应该在扩大窗口时还是缩小窗口时进行更新？

/* 滑动窗口算法框架 */
void slidingWindow(string s, string t) {
    unordered_map<char, int> need, window;
    for (char c : t) need[c]++;
    
    int left = 0, right = 0;
    /*如果一个字符进入窗口，应该增加 window 计数器；如果一个字符将移出窗口的时候，应该减少 window 计数器；当 valid 满足 need 时应该收缩窗口；应该在收缩窗口的时候更新最终结果。*/
    int valid = 0; 
    while (right < s.size()) {
        // c 是将移入窗口的字符
        char c = s[right];//注意下先后顺序，先记录要移出的字符，再去把坐标进行移动！！
        // 增大窗口
        right++;
        // 进行窗口内数据的一系列更新
        ...

        /*** debug 输出的位置 ***/
        printf("window: [%d, %d)\n", left, right);
        /********************/
        
        // 判断左侧窗口是否要收缩
        while (window needs shrink) {
        	.... if(....) {...}//此处进行对结果的处理更新！！
            // d 是将移出窗口的字符
            char d = s[left];
            // 缩小窗口
            left++;
            // 进行窗口内数据的一系列更新
            ...  //注意！这里的更新应该跟上面的更新对称，上面删除这里就添加，反之同理，代码应该是对称的！
        }
    }
}

其中两处 … 表示的更新窗口数据的地方，到时候你直接往里面填就行了。而且，这两个 … 处的操作分别是扩大和缩小窗口的更新操作，等会你会发现它们操作是完全对称的。
下面就直接上四道力扣原题来套这个框架，其中第一道题会详细说明其原理，后面四道就直接闭眼睛秒杀了。

1、最小覆盖子串

滑动窗口算法的思路是这样：
1、我们在字符串 S 中使用双指针中的左右指针技巧，初始化 left = right = 0，把索引左闭右开区间 [left, right) 称为一个「窗口」。

PS：理论上你可以设计两端都开或者两端都闭的区间，但设计为左闭右开区间是最方便处理的。因为这样初始化 left = right = 0 时区间 [0, 0) 中没有元素，但只要让 right 向右移动（扩大）一位，区间 [0, 1) 就包含一个元素 0 了。如果你设置为两端都开的区间，那么让 right 向右移动一位后开区间 (0, 1) 仍然没有元素；如果你设置为两端都闭的区间，那么初始区间 [0, 0] 就包含了一个元素。这两种情况都会给边界处理带来不必要的麻烦。

2、我们先不断地增加 right 指针扩大窗口 [left, right)，直到窗口中的字符串符合要求（包含了 T 中的所有字符）。
3、此时，我们停止增加 right，转而不断增加 left 指针缩小窗口 [left, right)，直到窗口中的字符串不再符合要求（不包含 T 中的所有字符了）。同时，每次增加 left，我们都要更新一轮结果。
4、重复第 2 和第 3 步，直到 right 到达字符串 S 的尽头。
【整个过程中】第 2 步相当于在寻找一个「可行解」，然后第 3 步在优化这个「可行解」，最终找到最优解，也就是最短的覆盖子串。左右指针轮流前进，窗口大小增增减减，窗口不断向右滑动，这就是「滑动窗口」这个名字的来历。
现在我们来看看这个滑动窗口代码框架怎么用：
1、初始化 window 和 need 两个哈希表，记录窗口中的字符和需要凑齐的字符：

unordered_map<char, int> need, window;
for (char c : t) need[c]++;

2、使用 left 和 right 变量初始化窗口的两端，不要忘了，区间 [left, right) 是左闭右开的，所以初始情况下窗口没有包含任何元素：

int left = 0, right = 0;
int valid = 0; 
while (right < s.size()) {
    // 开始滑动
}

其中 valid 变量表示窗口中满足 need 条件的字符个数，如果 valid 和 need.size 的大小相同，则说明窗口已满足条件，已经完全覆盖了串 T。
下面是完整代码：

string minWindow(string s, string t) {
    unordered_map<char, int> need, window;
    for (char c : t) need[c]++;

    int left = 0, right = 0;
    int valid = 0;
    // 记录最小覆盖子串的起始索引及长度
    int start = 0, len = INT_MAX;
    while (right < s.size()) {
        // c 是将移入窗口的字符
        char c = s[right];
        // 扩大窗口
        right++;
        // 进行窗口内数据的一系列更新
        if (need.count(c)) {
            window[c]++;
            if (window[c] == need[c])
                valid++;
        }

        // 判断左侧窗口是否要收缩
        while (valid == need.size()) {
            // 在这里更新最小覆盖子串--记录下来提取子串substr的左头和长度
            if (right - left < len) {
                start = left;
                len = right - left;
            }
            // d 是将移出窗口的字符
            char d = s[left];
            // 缩小窗口
            left++;
            // 进行窗口内数据的一系列更新
            if (need.count(d)) {
                if (window[d] == need[d]) valid--;
                window[d]--;
            }                    
        }
    }
    // 返回最小覆盖子串
    return len == INT_MAX ?"" : s.substr(start, len);
}

至此，应该可以完全理解这套框架了，滑动窗口算法又不难，就是细节问题让人烦得很。以后遇到滑动窗口算法，你就按照这框架写代码，保准没有 bug，还省事儿。

2、字符串排列

这种题目，是明显的滑动窗口算法，相当给你一个 S 和一个 T，请问你 S 中是否存在一个子串，包含 T 中所有字符且不包含其他字符？

// 判断 s 中是否存在 t 的排列
bool checkInclusion(string t, string s) {
    unordered_map<char, int> need, window;
    for (char c : t) need[c]++;

    int left = 0, right = 0;
    int valid = 0;
    while (right < s.size()) {
        char c = s[right];
        right++;
        // 进行窗口内数据的一系列更新
        if (need.count(c)) {
            window[c]++;
            if (window[c] == need[c])
                valid++;
        }

        // 判断左侧窗口是否要收缩
        while (right - left >= t.size()) {
            // 在这里判断是否找到了合法的子串
            if (valid == need.size())
                return true;
            char d = s[left];
            left++;
            // 进行窗口内数据的一系列更新
            if (need.count(d)) {
                if (window[d] == need[d])
                    valid--;
                window[d]--;
            }
        }
    }
    // 未找到符合条件的子串
    return false;
}

对于这道题的解法代码，基本上和最小覆盖子串一模一样，只需要改变两个地方：
1、本题移动 left 缩小窗口的时机是窗口大小大于 t.size() 时，应为排列嘛，显然长度应该是一样的。
2、当发现 valid == need.size() 时，就说明窗口中就是一个合法的排列，所以立即返回 true。
至于如何处理窗口的扩大和缩小，和最小覆盖子串完全相同。

3、找所有字母异位词

，这个所谓的字母异位词，不就是排列吗，搞个高端的说法就能糊弄人了吗？相当于，输入一个串 S，一个串 T，找到 S 中所有 T 的排列，返回它们的起始索引。

vector<int> findAnagrams(string s, string t) {
    unordered_map<char, int> need, window;
    for (char c : t) need[c]++;

    int left = 0, right = 0;
    int valid = 0;
    vector<int> res; // 记录结果
    while (right < s.size()) {
        char c = s[right];
        right++;
        // 进行窗口内数据的一系列更新
        if (need.count(c)) {
            window[c]++;
            if (window[c] == need[c]) 
                valid++;
        }
        // 判断左侧窗口是否要收缩
        while (right - left >= t.size()) {
            // 当窗口符合条件时，把起始索引加入 res
            if (valid == need.size())
                res.push_back(left);
            char d = s[left];
            left++;
            // 进行窗口内数据的一系列更新
            if (need.count(d)) {
                if (window[d] == need[d])
                    valid--;
                window[d]--;
            }
        }
    }
    return res;
}

4、最长无重复子串

int lengthOfLongestSubstring(string s) {
    unordered_map<char, int> window;

    int left = 0, right = 0;
    int res = 0; // 记录结果
    while (right < s.size()) {
        char c = s[right];
        right++;
        // 进行窗口内数据的一系列更新
        window[c]++;
        // 判断左侧窗口是否要收缩，收缩完成后一定保证窗口中没有重复
        while (window[c] > 1) {
            char d = s[left];
            left++;
            // 进行窗口内数据的一系列更新
            window[d]--;
        }
        // 在这里更新答案
        res = max(res, right - left);
    }
    return res;
}

这就是变简单了，连 need 和 valid 都不需要，而且更新窗口内数据也只需要简单的更新计数器 window 即可。

5、串联所有单词的子串(30.自己找的)

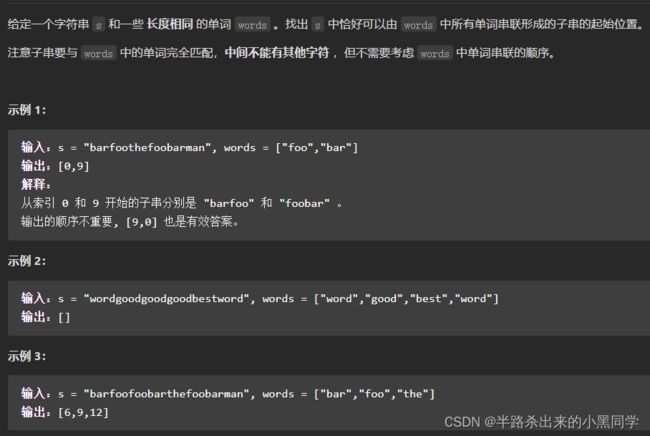
之前套用模板都是直接对字母进行处理，而这次是具有固定顺序的单词，其实一样的，只需要把单词当作一个“字母”即可。其中需要注意的就是，把一个单词当成字母，其是有不同形式的，如：

s ="barfaced"， words =["bar"]

其s中含有的单词不仅仅是bar、fac，还有arf、ace、rfa…
说到这里，应该就明白了，但是这里也是最容易混淆的。例如，当你把上面的bar看作是一个字母时，那么arf就不能再当作一个字母了，因为他们有重叠。然而在总体上看，他们其实是应该为两个字母。因此我们需要通过偏移划分开重叠的情况。

class Solution {
public:
    vector<int> findSubstring(string s, vector<string>& words) {
        //正常的need数组，记录下来我们需要什么"字母"
        unordered_map<string,int> record;
        vector<int>ans;
        for(auto word:words) record[word]++;
        int n =words[0].size();
        int length = n*words.size();
        //这个就是前文说到，为了防止单词划分成"字母"出现的重叠，而需要的偏移
        //注意这个偏移仅需要到0-n-1就行了，当为n时，相当于省略而不是偏移
        for(int i=0;i<n;++i)
        {
            //注意，由于每次偏移之后，都相当于一个新的单词改字母规则
            //所以要刷新窗口和其记录值vaild
            unordered_map<string,int> window;
            int vaild=0;
            int left = i,right = i;
            while(right <s.size())
            {
            string s_right = s.substr(right,n);
            //注意每次是要移动n个的，毕竟把n个字母组成的单词看作是一个字母
            right+= n;
            if(record.count(s_right))
            {
                window[s_right]++;
                if(window[s_right]==record[s_right]) vaild++;
            }
            //当需要右移窗口已经发现了足够的"单词"，开始从左缩小窗口
            while(vaild==record.size())
           {
                //当窗口的长度正好为所有words里面的单词长度时，其vaild仍满足，就可以输出了
                if(right-left == length) ans.push_back(left);
                string s_left = s.substr(left,n);
                left+= n;
                if(record.count(s_left))
                {
                    if(window[s_left]==record[s_left]) --vaild;
                    --window[s_left];
                }
            }
            }
        }
        return ans;
    }
};

6、数组里面有负数（单调队列）

由于 添加负数之后窗口的滑动就没有单向性了，因此无法使用滑动窗口解决。
而区间的和可以通过前缀和来解决，然后暴力枚举，但是时间复杂度会变成$n^2$，因此有两点需要我们来解决：

• 我们可以遍历加入前缀和，一旦发现前缀和前后相减的大小已经到达k，那么就可以滑动窗口排除前面的前缀和。
• 其次，由于我们前缀和利用区间的数，因此如果后面加进来的数小于前面的，那么再后面的去减这个队首，会得到更大的数，并且长度还小了，因此要去维护一个单调递减的队列，如果发现后面的数更小，那么就从后向前，把它前面比它大的都排走！

综上，第一个优化是为了求长度，第二个优化是为了之后的判断更容易。

class Solution {
public:
    int shortestSubarray(vector<int>& nums, int k) {
           int n = nums.size();
           vector<long long> pre_sum(n+1);
           for(int i = 1; i <= n; ++i) pre_sum[i] = pre_sum[i-1] + nums[i-1];
           int ans = INT_MAX;
           //维护一个单调队列来存前缀和的下标
           deque<int>dq;
           for(int i = 0; i <= n; ++i) {
               long long cur = pre_sum[i];
               while(!dq.empty() && cur - pre_sum[dq.front()] >= k) {
                   ans = min(ans, i - dq.front());
                   dq.pop_front();
               }
               while(!dq.empty() && cur <= pre_sum[dq.back()]) dq.pop_back();
               dq.push_back(i);
           }
            return ans == INT_MAX? -1:ans;
    }
};

五、一个方法团灭 LEETCODE 股票买卖问题

本文拒绝奇技淫巧，而是稳扎稳打，只用一种通用方法解决所用问题，以不变应万变。用状态机的技巧来解决，可以全部提交通过。不要觉得这个名词高大上，文学词汇而已，实际上就是 DP table，看一眼就明白了。

第一题是只进行一次交易，相当于 k = 1；第二题是不限交易次数，相当于 k = +infinity（正无穷）；第三题是只进行 2 次交易，相当于 k = 2；剩下两道也是不限次数，但是加了交易「冷冻期」和「手续费」的额外条件，其实就是第二题的变种，都很容易处理。

1、穷举框架

那么对于这道题，我们具体到每一天，看看总共有几种可能的「状态」，再找出每个「状态」对应的「选择」。我们要穷举所有「状态」，穷举的目的是根据对应的「选择」更新状态。听起来抽象，你只要记住「状态」和「选择」两个词就行，下面实操一下就很容易明白了。
每天都有三种「选择」：买入、卖出、无操作，我们用 buy, sell, rest 表示这三种选择。
这个问题有三个「状态」，第一个是天数，第二个是允许交易的最大次数，第三个是当前的持有状态（即之前说的 rest 的状态，我们不妨用 1 表示持有，0 表示没有持有）。然后我们用一个三维数组就可以装下这几种状态的全部组合：

dp[i][k][0 or 1]
0 <= i <= n - 1, 1 <= k <= K
n 为天数，大 K 为交易数的上限，0 和 1 代表是否持有股票。
此问题共 n × K × 2 种状态，全部穷举就能搞定。

for 0 <= i < n:
    for 1 <= k <= K:
        for s in {0, 1}://理论有三个for，但是0和1可以直接列举，所以不用三个循环
            dp[i][k][s] = max(buy, sell, rest)

而且我们可以用自然语言描述出每一个状态的含义，比如说 dp[3][2][1] 的含义就是：今天是第三天，我现在手上持有着股票，至今最多进行 2 次交易。
而我们想求的最终答案是 dp[n - 1][K][0]，即最后一天，最多允许 K 次交易，最多获得多少利润。

读者可能问为什么不是 dp[n - 1][K][1]？因为 dp[n - 1][K][1] 代表到最后一天手上还持有股票，dp[n - 1][K][0] 表示最后一天手上的股票已经卖出去了，很显然后者得到的利润一定大于前者。

记住如何解释「状态」，一旦你觉得哪里不好理解，把它翻译成自然语言就容易理解了。

2、状态转移框架

只看「持有状态」，可以画个状态转移图：
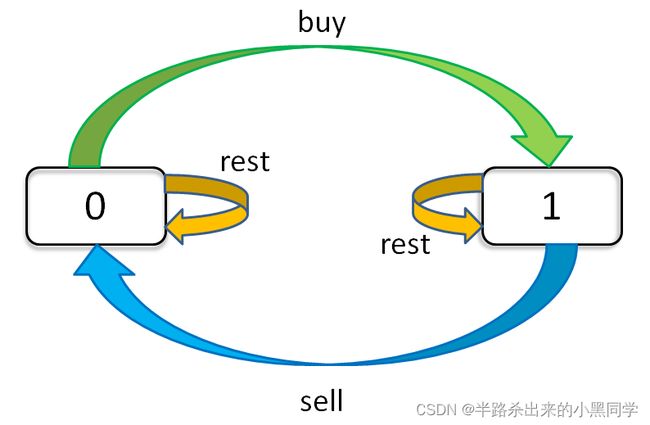根据这个图，我们来写一下状态转移方程：

dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
              max( 今天选择 rest,        今天选择 sell       )

解释：今天我没有持有股票，有两种可能，我从这两种可能中求最大利润：
1、我昨天就没有持有，且截至昨天最大交易次数限制为 k；然后我今天选择 rest，所以我今天还是没有持有，最大交易次数限制依然为 k。
2、我昨天持有股票，且截至昨天最大交易次数限制为 k；但是今天我 sell 了，所以我今天没有持有股票了，最大交易次数限制依然为 k。

dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
              max( 今天选择 rest,         今天选择 buy         )

解释：今天我持有着股票，最大交易次数限制为 k，那么对于昨天来说，有两种可能，我从这两种可能中求最大利润：
1、我昨天就持有着股票，且截至昨天最大交易次数限制为 k；然后今天选择 rest，所以我今天还持有着股票，最大交易次数限制依然为 k。
2、我昨天本没有持有，且截至昨天最大交易次数限制为 k - 1；但今天我选择 buy，所以今天我就持有股票了，最大交易次数限制为 k。

这里着重提醒一下，时刻牢记「状态」的定义，状态 k 的定义并不是「已进行的交易次数」，而是「最大交易次数的上限限制」。如果确定今天进行一次交易，且要保证截至今天最大交易次数上限为 k，那么昨天的最大交易次数上限必须是 k - 1。

注意 k 的限制，在选择 buy 的时候相当于开启了一次交易，那么对于昨天来说，交易次数的上限 k 应该减小 1。

修正：以前我以为在 sell 的时候给 k 减小 1 和在 buy 的时候给 k 减小 1 是等效的，但细心的读者向我提出质疑，经过深入思考我发现前者确实是错误的，因为交易是从 buy 开始，如果 buy 的选择不改变交易次数 k 的话，会出现交易次数超出限制的的错误。

现在，我们已经完成了动态规划中最困难的一步：状态转移方程。如果之前的内容你都可以理解，那么你已经可以秒杀所有问题了，只要套这个框架就行了。不过还差最后一点点，就是定义 base case，即最简单的情况（其实找baseline就是进入循环，看看哪些情况会报错需要初始值）。

dp[-1][...][0] = 0
解释：因为 i 是从 0 开始的，所以 i = -1 意味着还没有开始，这时候的利润当然是 0。
dp[-1][...][1] = -infinity
解释：还没开始的时候，是不可能持有股票的。
因为我们的算法要求一个最大值，所以初始值设为一个最小值，方便取最大值。
dp[...][0][0] = 0
解释：因为 k 是从 1 开始的，所以 k = 0 意味着根本不允许交易，这时候利润当然是 0。
dp[...][0][1] = -infinity
解释：不允许交易的情况下，是不可能持有股票的。
因为我们的算法要求一个最大值，所以初始值设为一个最小值，方便取最大值。

总结如下：

base case：
dp[-1][...][0] = dp[...][0][0] = 0
dp[-1][...][1] = dp[...][0][1] = -infinity

状态转移方程：
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])

3、秒杀题目

第一题–相当于 k = 1 的情况：

直接套状态转移方程，根据 base case，可以做一些化简。此处直接给出代码（需要注意的是：这样处理 base case 很麻烦，而且注意一下状态转移方程，新状态只和相邻的一个状态有关，所以可以用前文 动态规划的降维打击：空间压缩技巧，不需要用整个 dp 数组，只需要一个变量储存相邻的那个状态就足够了，这样可以把空间复杂度降到 O(1)）：

// 原始版本
int maxProfit_k_1(vector<int> prices) {
    int n = prices.size();
    vector<vector<int>> dpa(n, vector<int>(2, 0));;
    for (int i = 0; i < n; i++) {
    	// base case
        if (i - 1 == -1) {
            dp[i][0] = 0;
            dp[i][1] = -prices[i];//注意第一天也是可以买的！
            continue;
        }
        dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]);
        dp[i][1] = max(dp[i-1][1], -prices[i]);//注意，只允许交易一次，因此手上的现金数就是当天的股价的相反数）。这样防止你买了再卖，因此每次购买都是重新开始计算！！！
    }
    return dp[n - 1][0];
}
// 空间复杂度优化版本
int maxProfit_k_1(vector<int> prices) {
    int n = prices.size();
    // base case: dp[-1][0] = 0, dp[-1][1] = -infinity
    int dp_i_0 = 0, dp_i_1 = INT_MIN;
    for (int i = 0; i < n; i++) {
        // dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
        dp_i_0 = max(dp_i_0, dp_i_1 + prices[i]);
        // dp[i][1] = max(dp[i-1][1], -prices[i])
        dp_i_1 = max(dp_i_1, -prices[i]);
    }
    return dp_i_0;
}

第二题–相当于 k 为正无穷的情况：

因此`我们发现数组中的 k 已经不会改变了，也就是说不需要记录 k 这个状态了：

dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])`

因此

// 原始版本
int maxProfit_k_1(vector<int> prices) {
    int n = prices.size();
    vector<vector<int>> dpa(n, vector<int>(2, 0));;
    for (int i = 0; i < n; i++) {
    	// base case
        if (i - 1 == -1) {
            dp[i][0] = 0;
            dp[i][1] = -prices[i];
            continue;
        }
        dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]);
        dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i]);
    }
    return dp[n - 1][0];
}
// 空间复杂度优化版本
int maxProfit_k_1(vector<int> prices) {
    int n = prices.size();
    // base case: dp[-1][0] = 0, dp[-1][1] = -infinity
    int dp_i_0 = 0, dp_i_1 = INT_MIN;
    for (int i = 0; i < n; i++) {
     int temp = dp_i_0;
        // dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
        dp_i_0 = max(dp_i_0, dp_i_1 + prices[i]);
        // dp[i][1] = max(dp[i-1][1], -prices[i])
        dp_i_1 = max(dp_i_1, temp-prices[i]);
    }
    return dp_i_0;
}

第三题-- k 为正无穷，但含有交易冷冻期的情况：

和上一道题一样的，只不过每次 sell 之后要等一天才能继续交易，只要把这个特点融入上一题的状态转移方程即可：

dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-2][0] - prices[i])
解释：第 i 天选择 buy 的时候，要从 i-2 的状态转移，而不是 i-1 。

注意baseline也要考虑i=0和i=1两种情况：

// 原始版本
int maxProfit_k_1(vector<int> prices) {
    int n = prices.size();
    vector<vector<int>> dpa(n, vector<int>(2, 0));;
    for (int i = 0; i < n; i++) {
    	// base case1
        if (i - 1 == -1) {
            dp[i][0] = 0;
            dp[i][1] = -prices[i];
            continue;
        }
        // base case1
         if (i - 2 == -1) {
            dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]);
            // i - 2 小于 0 时根据状态转移方程推出对应 base case
            dp[i][1] = max(dp[i-1][1], -prices[i]);
            //   dp[i][1] 
            // = max(dp[i-1][1], dp[-1][0] - prices[i])
            // = max(dp[i-1][1], 0 - prices[i])
            // = max(dp[i-1][1], -prices[i])
            continue;
        }
        dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]);
        dp[i][1] = max(dp[i-1][1], dp[i-2][0] - prices[i]);//其实是-1-1，从正常的昨天变成隔一天的昨天
    }
    return dp[n - 1][0];
}
// 空间复杂度优化版本
int maxProfit_k_1(vector<int> prices) {
    int n = prices.size();
    // base case: dp[-1][0] = 0, dp[-1][1] = -infinity
    int dp_i_0 = 0, dp_i_1 = INT_MIN;
    int dp_pre_0 = 0; // 代表 dp[i-2][0]
    for (int i = 0; i < n; i++) {
        // dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
        dp_i_0 = max(dp_i_0, dp_i_1 + prices[i]);
        // dp[i][1] = max(dp[i-1][1], -prices[i])
        dp_i_1 = max(dp_i_1, dp_pre_0 -prices[i]);
    }
    return dp_i_0;
}

第四题-- k 为正无穷且考虑交易手续费的情况：

每次交易要支付手续费，只要把手续费从利润中减去即可，改写方程：

dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i] - fee)
解释：相当于买入股票的价格升高了。
在第一个式子里减也是一样的，相当于卖出股票的价格减小了。

如果直接把 fee 放在第一个式子里减，会有一些测试用例无法通过，错误原因是整型溢出而不是思路问题。

// 原始版本
int maxProfit_k_1(vector<int> prices, int fee) {
    int n = prices.size();
    vector<vector<int>> dpa(n, vector<int>(2, 0));;
    for (int i = 0; i < n; i++) {
    	// base case
        if (i - 1 == -1) {
            dp[i][0] = 0;
            dp[i][1] = -prices[i] - free;
            continue;
        }
        dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]);
        dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i] - free);
    }
    return dp[n - 1][0];
}
// 空间复杂度优化版本
int maxProfit_k_1(vector<int> prices) {
    int n = prices.size();
    // base case: dp[-1][0] = 0, dp[-1][1] = -infinity
    int dp_i_0 = 0, dp_i_1 = INT_MIN;
    for (int i = 0; i < n; i++) {
     int temp = dp_i_0;
        // dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
        dp_i_0 = max(dp_i_0, dp_i_1 + prices[i]);
        // dp[i][1] = max(dp[i-1][1], -prices[i])
        dp_i_1 = max(dp_i_1, temp-prices[i]);
    }
    return dp_i_0;
}

第五题-- k = 2 的情况：

k = 2 和前面题目的情况稍微不同，因为上面的情况都和 k 的关系不太大：要么 k 是正无穷，状态转移和 k 没关系了；要么 k =
1，跟 k = 0 这个 base case 挨得近，最后也没有存在感。这道题 k = 2 和后面要讲的 k 是任意正整数的情况中，对 k
的处理就凸显出来了，我们直接写代码，边写边分析原因。

// 原始版本
int maxProfit_k_2(vector<int> prices) {
    int max_k = 2, n = prices.length;
    vector<vector<vector<int>>> dp(n,vector<vector<int>>(max_k+1,vector<int>(2,0)));
    for (int i = 0; i < n; i++) {
        for (int k = max_k; k >= 1; k--)//这里k递减递加都是可以的，递减符合逻辑
         {
         // 处理 base case
            if (i - 1 == -1) {
                dp[i][k][0] = 0;
                dp[i][k][1] = -prices[i];
                continue;
            }
            dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);
            dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]);
        }
    }
    // 穷举了 n × max_k × 2 个状态，正确。
    return dp[n - 1][max_k][0];
}

// 状态转移方程：
// dp[i][2][0] = max(dp[i-1][2][0], dp[i-1][2][1] + prices[i])
// dp[i][2][1] = max(dp[i-1][2][1], dp[i-1][1][0] - prices[i])
// dp[i][1][0] = max(dp[i-1][1][0], dp[i-1][1][1] + prices[i])
// dp[i][1][1] = max(dp[i-1][1][1], -prices[i])

// 空间复杂度优化版本--这里 k 取值范围比较小，所以也可以不用 for 循环，直接把 k = 1 和 2 的情况全部列举出来也可以
int maxProfit_k_2(int[] prices) {
    // base case
    int dp_i10 = 0, dp_i11 = Integer.MIN_VALUE;
    int dp_i20 = 0, dp_i21 = Integer.MIN_VALUE;
    for (int price : prices) {
        dp_i20 = Math.max(dp_i20, dp_i21 + price);
        dp_i21 = Math.max(dp_i21, dp_i10 - price);
        dp_i10 = Math.max(dp_i10, dp_i11 + price);
        dp_i11 = Math.max(dp_i11, -price);
    }
    return dp_i20;
}

第六题-- k 可以是题目给定的任何数的情况：

有了上一题 k = 2 的铺垫，这题应该和上一题的第一个解法没啥区别，你把上一题的 k = 2 换成题目输入的 k 就行了。

一次交易由买入和卖出构成，至少需要两天。所以说有效的限制 k 应该不超过 n/2，如果超过，就没有约束作用了，相当于 k 没有限制的情况，而这种情况是之前解决过的

int maxProfit_k_any(int max_k, vector<int> prices) {
    int n = prices.size();
    if (n <= 0) {
        return 0;
    }
    if (max_k > n / 2) {
        // 复用之前交易次数 k 没有限制的情况
        return maxProfit_k_inf(prices);
    }

    // base case：
    // dp[-1][...][0] = dp[...][0][0] = 0
    // dp[-1][...][1] = dp[...][0][1] = -infinity
    vector<vector<vector<int>>> dp(n,vector<vector<int>>(max_k+1,vector<int>(2,0)));
    // k = 0 时的 base case
    for (int i = 0; i < n; i++) {
        dp[i][0][1] = MIN_INT;
        dp[i][0][0] = 0;
    }

    for (int i = 0; i < n; i++) 
        for (int k = max_k; k >= 1; k--) {
            if (i - 1 == -1) {
                // 处理 i = -1 时的 base case
                dp[i][k][0] = 0;
                dp[i][k][1] = -prices[i];
                continue;
            }
            dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);
            dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]);     
        }
    return dp[n - 1][max_k][0];
}

万法归一

现在你已经过了九九八十一难中的前八十难，最后我还要再难为你一下，请你实现如下函数：

int maxProfit_all_in_one(int max_k, vector<int> prices, int cooldown, int fee);

输入股票价格数组 prices，你最多进行 max_k 次交易，每次交易需要额外消耗 fee 的手续费，而且每次交易之后需要经过 cooldown 天的冷冻期才能进行下一次交易，请你计算并返回可以获得的最大利润。
其实，我们只要把之前实现的几种代码掺和到一块，在 base case 和状态转移方程中同时加上 cooldown 和 fee 的约束就行了：

// 同时考虑交易次数的限制、冷冻期和手续费
int maxProfit_all_in_one(int max_k,vector<int>prices, int cooldown, int fee) {
    int n = prices.size();
    if (n <= 0) {
        return 0;
    }
    if (max_k > n / 2) {
        // 交易次数 k 没有限制的情况
        return maxProfit_k_inf(prices, cooldown, fee);
    }

    vector<vector<vector<int>>> dp(n,vector<vector<int>>(max_k+1,vector<int>(2,0)));
    // k = 0 时的 base case
    for (int i = 0; i < n; i++) {
        dp[i][0][1] = INT_MIN;
        dp[i][0][0] = 0;
    }
    for (int i = 0; i < n; i++) 
        for (int k = max_k; k >= 1; k--) {
            if (i - 1 == -1) {
                // base case 1
                dp[i][k][0] = 0;
                dp[i][k][1] = -prices[i] - fee;
                continue;
            }

            // 包含 cooldown 的 base case
            if (i - cooldown - 1 < 0) {
                // base case 2
                dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);
                // 别忘了减 fee
                dp[i][k][1] = max(dp[i-1][k][1], -prices[i] - fee);
                continue;
            }
            dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);
            // 同时考虑 cooldown 和 fee
            dp[i][k][1] = max(dp[i-1][k][1], dp[i-cooldown-1][k-1][0] - prices[i] - fee);     
        }
    return dp[n - 1][max_k][0];
}

// k 无限制，包含手续费和冷冻期
int maxProfit_k_inf(vector<int> prices, int cooldown, int fee) {
    int n = prices.size();
    vector<vector<int>> dp(n,vector<int>(2,0));
    for (int i = 0; i < n; i++) {
        if (i - 1 == -1) {
            // base case 1
            dp[i][0] = 0;
            dp[i][1] = -prices[i] - fee;
            continue;
        }

        // 包含 cooldown 的 base case
        if (i - cooldown - 1 < 0) {
            // base case 2
            dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]);
            // 别忘了减 fee
            dp[i][1] = max(dp[i-1][1], -prices[i] - fee);
            continue;
        }
        dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
        // 同时考虑 cooldown 和 fee
        dp[i][1] = max(dp[i - 1][1], dp[i - cooldown - 1][0] - prices[i] - fee);
    }
    return dp[n - 1][0];
}

关键就在于列举出所有可能的「状态」，然后想想怎么穷举更新这些「状态」。一般用一个多维 dp 数组储存这些状态，从 base case 开始向后推进，推进到最后的状态，就是我们想要的答案。想想这个过程，你是不是有点理解「动态规划」这个名词的意义了呢？

六、一个方法团灭 LEETCODE 打家劫舍问题

第一题

题目很容易理解，而且动态规划的特征很明显。我们前文 动态规划详解 做过总结，解决动态规划问题就是找「状态」和「选择」，仅此而已。
你面前房子的索引就是状态，抢和不抢就是选择。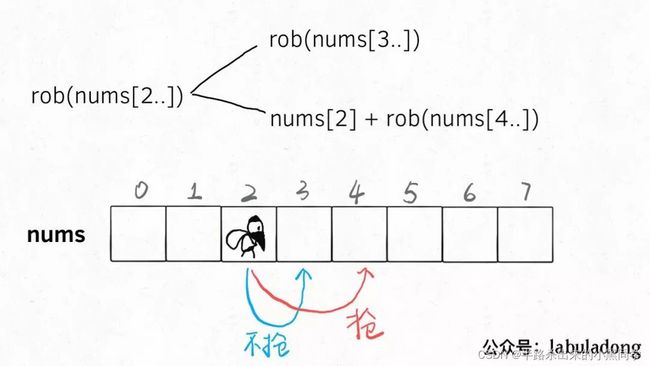
在两个选择中，每次都选更大的结果，最后得到的就是最多能抢到的 money：

// 主函数
int rob(vector<int> nums) {
    return dp(nums, 0);
}
// 返回 nums[start..] 能抢到的最大值
int dp(vector<int> nums, int start) {
    if (start >= nums.size()) {
        return 0;
    }
    int res = max(
            // 不抢，去下家
            dp(nums, start + 1), 
            // 抢，去下下家
            nums[start] + dp(nums, start + 2)
        );
    return res;
}

明确了状态转移，就可以发现对于同一start位置，是存在重叠子问题的，比如下图：
盗贼有多种选择可以走到这个位置，如果每次到这都进入递归，岂不是浪费时间？所以说存在重叠子问题，可以用备忘录进行优化：

// 主函数
vector<int>memo;
int rob(vector<int> nums) {
	// 初始化备忘录
	memo.resize(nums.size(),-1);
	// 强盗从第 0 间房子开始抢劫
    return dp(nums, 0);
}
// 返回 nums[start..] 能抢到的最大值
int dp(vector<int> nums, int start) {
    if (start >= nums.size()) {
        return 0;
    }
    // 避免重复计算
     if (memo[start] != -1) return memo[start];
    int res = max(
            // 不抢，去下家
            dp(nums, start + 1), 
            // 抢，去下下家
            nums[start] + dp(nums, start + 2)
        );
    memo[start] = res;// 记入备忘录
    return res;
}

这就是自顶向下的动态规划解法，我们也可以略作修改，写出自底向上的解法：

//原始版本
int rob(vector<int> nums) {
    int n = nums.size();
    // dp[i] = x 表示：
    // 从第 i 间房子开始抢劫，最多能抢到的钱为 x
    // base case: dp[n] = 0
    vector<int> dp(n + 2, 0);
    for (int i = n - 1; i >= 0; i--) {
        dp[i] = max(dp[i + 1], nums[i] + dp[i + 2]);
    }
    return dp[0];
}
//优化空间复杂度到1的版本
int rob(vector<int> nums) {
    int n = nums.size();
    // 记录 dp[i+1] 和 dp[i+2]
    int dp_i_1 = 0, dp_i_2 = 0;
    // 记录 dp[i]
    int dp_i = 0; 
    for (int i = n - 1; i >= 0; i--) {
        dp_i = max(dp_i_1, nums[i] + dp_i_2);
        dp_i_2 = dp_i_1;
        dp_i_1 = dp_i;
    }
    return dp_i;
}

第二题

注意，如果仅仅是环形数组，可以通过单调栈来解决。
这道题目和第一道描述基本一样，强盗依然不能抢劫相邻的房子，输入依然是一个数组，但是告诉你这些房子不是一排，而是围成了一个圈。

也就是说，现在第一间房子和最后一间房子也相当于是相邻的，不能同时抢。比如说输入数组nums=[2,3,2]，算法返回的结果应该是 3 而不是
4，因为开头和结尾不能同时被抢。

首先，首尾房间不能同时被抢，那么只可能有三种不同情况：要么都不被抢；要么第一间房子被抢最后一间不抢；要么最后一间房子被抢第一间不抢。（由于数组里面都是非负，所以只考虑情况一和二即可）所以只需对之前的解法稍作修改即可：

int rob(vector<int> nums) {
    int n = nums.size();
    if (n == 1) return nums[0];
    //下面就是对应着两种方法。
    return max(robRange(nums, 0, n - 2), 
                    robRange(nums, 1, n - 1));
}

// 仅计算闭区间 [start,end] 的最优结果
int robRange(vector<int> nums, int start, int end) {
    int dp_i_1 = 0, dp_i_2 = 0;
    int dp_i = 0;
    for (int i = end; i >= start; i--) {
        dp_i = max(dp_i_1, nums[i] + dp_i_2);
        dp_i_2 = dp_i_1;
        dp_i_1 = dp_i;
    }
    return dp_i;
}

第三题

第三题又想法设法地变花样了，此强盗发现现在面对的房子不是一排，不是一圈，而是一棵二叉树！房子在二叉树的节点上，相连的两个房子不能同时被抢劫：

整体的思路完全没变，还是做抢或者不抢的选择，取收益较大的选择。甚至我们可以直接按这个套路写出代码：

unordered_map<TreeNode*,int> record;
public int rob(TreeNode* root) {
    if (root == nullptr) return 0;
    // 利用备忘录消除重叠子问题
    if (record.find(root)!=memo.end()) 
        return record[root];
    // 抢，然后去下下家
 	int do_it = root->val
        + (root->left == nullptr? 0:rob(root->left->left)+rob(root->left-		>right))
        + (root->right == nullptr? 0:rob(root->right->left)+rob(root->right->right));
    // 不抢，然后去下家
    int not_do = rob(root->left) + rob(root->right);

    int res = max(do_it, not_do);
    record[root] = res;
    return res;
}

七、一个函数秒杀 2Sum 3Sum 4Sum 问题

1、twoSum 问题

【题目】如果假设输入一个数组 nums 和一个目标和 target，请你返回 nums 中能够凑出 target 的两个元素的值，比如输入 nums = [5,3,1,6], target = 9，那么算法返回两个元素 [3,6]。可以假设只有且仅有一对儿元素可以凑出 target。
【解法一】我们可以先对 nums 排序，然后利用前文「双指针技巧汇总」写过的左右双指针技巧，从两端相向而行就行了。不过我们要继续魔改题目，把这个题目变得更泛化，更困难一点：
nums 中可能有多对儿元素之和都等于 target，请你的算法返回所有和为 target 的元素对儿，其中不能出现重复。
比如说输入为 nums = [1,3,1,2,2,3], target = 4，那么算法返回的结果就是：[[1,3],[2,2]]。
对于修改后的问题，关键难点是现在可能有多个和为 target 的数对儿，还不能重复，比如上述例子中 [1,3] 和 [3,1] 就算重复，只能算一次。因此，再使用双指针的时候要跳过重复的：

vector<vector<int>> twoSumTarget(vector<int>& nums, int target) {
    // nums 数组必须有序
    sort(nums.begin(), nums.end());
    int lo = 0, hi = nums.size() - 1;
    vector<vector<int>> res;
    while (lo < hi) {
        int sum = nums[lo] + nums[hi];
        int left = nums[lo], right = nums[hi];
        if (sum < target) {
        // 跳过所有重复的元素
            while (lo < hi && nums[lo] == left) lo++;
        } else if (sum > target) {
        // 跳过所有重复的元素
            while (lo < hi && nums[hi] == right) hi--;
        } else {
            res.push_back({left, right});
            // 跳过所有重复的元素
            while (lo < hi && nums[lo] == left) lo++;
            while (lo < hi && nums[hi] == right) hi--;
        }
    }
    return res;
}

这样，一个通用化的 twoSum 函数就写出来了，请确保你理解了该算法的逻辑，我们后面解决 3Sum 和 4Sum 的时候会复用这个函数。

2、3Sum 问题

这样，我们再泛化一下题目，不要光和为 0 的三元组了，计算和为 target 的三元组吧，同上面的 twoSum 一样，也不允许重复的结果：
定了第一个数字之后，剩下的两个数字可以是什么呢？其实就是和为 target - nums[i] 的两个数字呗，那不就是 twoSum 函数解决的问题么

/* 从 nums[start] 开始，计算有序数组
 * nums 中所有和为 target 的二元组 */
vector<vector<int>> twoSumTarget(
    vector<int>& nums, int start, int target) {
    // 左指针改为从 start 开始，其他不变
    int lo = start, hi = nums.size() - 1;
    vector<vector<int>> res;
    while (lo < hi) {
        ...
    }
    return res;
}

/* 计算数组 nums 中所有和为 target 的三元组 */
vector<vector<int>> threeSumTarget(vector<int>& nums, int target) {
    // 数组得排个序
    sort(nums.begin(), nums.end());
    int n = nums.size();
    vector<vector<int>> res;
    // 穷举 threeSum 的第一个数
    for (int i = 0; i < n; i++) {
        // 对 target - nums[i] 计算 twoSum
        vector<vector<int>> 
            tuples = twoSumTarget(nums, i + 1, target - nums[i]);
        // 如果存在满足条件的二元组，再加上 nums[i] 就是结果三元组
        for (vector<int>& tuple : tuples) {
            tuple.push_back(nums[i]);
            res.push_back(tuple);
        }
        // 跳过第一个数字重复的情况，否则会出现重复结果
        while (i < n - 1 && nums[i] == nums[i + 1]) i++;
    }
    return res;
}

关键点在于，不能让第一个数重复，至于后面的两个数，我们复用的 twoSum 函数会保证它们不重复。所以代码中必须用一个 while 循环来保证 3Sum 中第一个元素不重复。

3、4Sum 问题

都到这份上了，4Sum 完全就可以用相同的思路：穷举第一个数字，然后调用 3Sum 函数计算剩下三个数，最后组合出和为 target 的四元组。

vector<vector<int>> fourSum(vector<int>& nums, int target) {
    // 数组需要排序
    sort(nums.begin(), nums.end());
    int n = nums.size();
    vector<vector<int>> res;
    // 穷举 fourSum 的第一个数
    for (int i = 0; i < n; i++) {
        // 对 target - nums[i] 计算 threeSum
        vector<vector<int>> 
            triples = threeSumTarget(nums, i + 1, target - nums[i]);
        // 如果存在满足条件的三元组，再加上 nums[i] 就是结果四元组
        for (vector<int>& triple : triples) {
            triple.push_back(nums[i]);
            res.push_back(triple);
        }
        // fourSum 的第一个数不能重复
        while (i < n - 1 && nums[i] == nums[i + 1]) i++;
    }
    return res;
}

/* 从 nums[start] 开始，计算有序数组
 * nums 中所有和为 target 的三元组 */
vector<vector<int>> 
    threeSumTarget(vector<int>& nums, int start, int target) {
        int n = nums.size();
        vector<vector<int>> res;
        // i 从 start 开始穷举，其他都不变
        for (int i = start; i < n; i++) {
            ...
        }
        return res;

完整的AC例题

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        vector<vector<int>> ans;
        sort(nums.begin(),nums.end());
        int n = nums.size();
        for(int i=0;i<n-2;++i)
        {
            vector<vector<int>> tem  = threeSum(nums,target-nums[i],i+1);
            for(auto &a:tem)
            {
                a.push_back(nums[i]);
                ans.push_back(a);
            }
            while(i<n-2 && nums[i]==nums[i+1]) i++;
        }
        return ans;
    }
    //不改成longlong会爆炸
    vector<vector<int>> threeSum(vector<int>& nums, long long target,int start) {
        vector<vector<int>> ans;
        int n = nums.size();
        for(int i=start;i<n-1;++i)
        {
            vector<vector<int>> tem = twoSum(nums,target-nums[i],i+1);
            for(auto & a:tem)
            {
                a.push_back(nums[i]);
                ans.push_back(a);
            }
            while(i<n-1 && nums[i]==nums[i+1]) i++;
        }
        return ans;
    }
    vector<vector<int>> twoSum(vector<int>& nums, long long target,int start) {
        vector<vector<int>> ans;
        int left = start,right = nums.size()-1;
        while(left<right)
        {
            int left_v = nums[left],right_v = nums[right];
            if(left_v+right_v==target)
            {
                ans.push_back({nums[left],nums[right]});
                while(left<right && nums[left]==left_v) left++;
                while(left<right && nums[right]==right_v) right--;
            }
            else if(left_v+right_v>target)
            {
                while(left<right && nums[right]==right_v)right--;
            }
            else{while(left<right && nums[left]==left_v)left++;}
        }
        return ans;
    }
};

4、！！！100Sum 问题？！！！

其实我们可以观察上面这些解法，统一出一个 nSum 函数(这类嵌套着的，明显可以用递归来统一一下)：其实就是以最终的滑动窗口2sum为基准，其他的多个都递归到最后的2sum再进行计算（只不过目标值是减去当前遍历到的值的）。

/* 注意：调用这个函数之前一定要先给 nums 排序 */
// 在主函数里进行。sort(nums.begin(), nums.end());
vector<vector<int>> nSumTarget(
    vector<int>& nums, int n, int start, int target) {

    int sz = nums.size();
    vector<vector<int>> res;
    // 至少是 2_Sum，且数组大小不应该小于 n
    if (n < 2 || sz < n) return res;
    // 2Sum 是 base case
    if (n == 2) {
        // 双指针那一套操作
        int lo = start, hi = sz - 1;
        while (lo < hi) {
            int sum = nums[lo] + nums[hi];
            int left = nums[lo], right = nums[hi];
            if (sum < target) {
                while (lo < hi && nums[lo] == left) lo++;
            } else if (sum > target) {
                while (lo < hi && nums[hi] == right) hi--;
            } else {
                res.push_back({left, right});
                while (lo < hi && nums[lo] == left) lo++;
                while (lo < hi && nums[hi] == right) hi--;
            }
        }
    } else {
        // n > 2 时，递归计算 (n-1)Sum 的结果
        for (int i = start; i < sz; i++) {
            vector<vector<int>> 
                sub = nSumTarget(nums, n - 1, i + 1, target - nums[i]);
            for (vector<int>& arr : sub) {
                // (n-1)Sum 加上 nums[i] 就是 nSum
                arr.push_back(nums[i]);
                res.push_back(arr);
            }
            while (i < sz - 1 && nums[i] == nums[i + 1]) i++;
        }
    }
    return res;
}