一文看懂快慢指针(Fast-Slow Pointer)求解数组中的重复数字
数组中寻找重复的数字是一道非常好玩的题。各种约束、各种复杂度的要求,会导致各种不同的解法,其中不乏巧妙的思路。
快慢指针方法代码非常简洁,时空复杂度又都很低,很巧妙,但看到的所有解释都有点跳跃,比较难以理解,所以这里详解一下,希望能明白畅达。
题目背景
题目背景:
给定长度为 N + 1 N+1 N+1的数组,其中所有数字都在[1, N]之间,由容斥原理,一定至少有两个数字是重复的。找出这个重复数字。
把各种情况的解法汇总一下。
O T O_T OT:时间复杂度; O S O_S OS:空间复杂度;M/NM:允许/不允许修改原数组。
首先列出传统解法,老生常谈:
| 约束\题目场景 | 若干重复数字,找出任意一个 | 只有一个重复数字 |
|---|---|---|
| O T ( N 2 ) O_T(N^2) OT(N2), O S ( 1 ) O_S(1) OS(1), NM | 遍历 | 遍历 |
| O T ( N log N ) O_T(N \log N) OT(NlogN), O S ( N ) O_S(N) OS(N), NM | 排序 | 排序 |
| O T ( N log N ) O_T(N \log N) OT(NlogN), O S ( 1 ) O_S(1) OS(1), M | 原位排序 | 原位排序 |
接下来是有意思的部分。“-”是指其他解法可以解决,无须赘述。例如, O T ( N ) O_T(N) OT(N)的解法肯定满足 O T ( N log N ) O_T(N\log N) OT(NlogN),NM的解法也肯定满足M。
| 约束\题目场景 | 只有一个重复数字 | 若干重复数字,找出任意一个 |
|---|---|---|
| O T ( N log N ) O_T(N\log N) OT(NlogN), O S ( 1 ) O_S(1) OS(1), NM | - | 二分范围寻找 |
| O T ( N ) O_T(N) OT(N), O S ( 1 ) O_S(1) OS(1), M | - | 下标标记法 |
| O T ( N ) O_T(N) OT(N), O S ( 1 ) O_S(1) OS(1), NM | 加和法;异或法 | 快慢指针 |
除了快慢指针之外,其他方法的名字都不是公认冠名,这里简单解释一下:
- 加和法:只有一个数字重复,则其他数之和必定等于1…N的等差数列之和 ( N + 1 ) N / 2 (N+1)N/2 (N+1)N/2,遍历数组求和,减去 ( N + 1 ) N / 2 (N+1)N/2 (N+1)N/2即可;
- 异或法:A^A=0,因此先计算1~N的异或结果,再依次和数组中的数求异或,其他数字均被消去,留下的就是出现过两次的数。
- 下标标记法:从头遍历,若当前数nums[i]=x,则令nums[x] +=N。由于数组最大值为N,因此如果发现nums[x]>N,意味着x出现了两次(之前已经被加过一次了)。为了叙述简洁,略去一些细节。
- 二分范围查找:不允许修改数组,又要求空间为1,难道只能以 O T ( N 2 ) O_T(N^2) OT(N2)的时间复杂度遍历了吗?不。重复数字一定在[1, N]内,我们可以对值域进行二分查找。由鸽巢原理,至少有一个半区的数的数量大于半区范围。如[1,2,3,3,4],范围是[1,4],分为[1,2], [3,4]两个半区。[3,4]半区范围是2,但有3个数字满足要求,则必有重复。如此下去,时间复杂度是 O T ( N log N ) O_T(N\log N) OT(NlogN)。
LeetCode中有很多相关的题目,这里说的是287. Find the Duplicate Number。原题的时间复杂度要求是 O ( N 2 ) O(N^2) O(N2),空间复杂度是 O ( 1 ) O(1) O(1),不允许修改原数组。 O ( N 2 ) O(N^2) O(N2)太慢了,引出我们今天的主角
快慢指针
快慢指针,顾名思义,在链表中,维持两个指针,跳跃速度不同(A跳一步,B就跳两步)。他能做的事情很多,最直观的是寻找链表的中点。还可以判断链表是否有环等等。这里我们先解释快慢指针算法,然后分析它的复杂度。
四行代码
先来看“速度快过100% Submission,空间小于100% Submission”的代码!
public static int findDuplicate(int[] nums) {
int slow = nums[0], fast = nums[slow];
for (; slow != fast; slow = nums[slow], fast = nums[nums[fast]]);
for (slow = 0; nums[slow] != nums[fast]; fast = nums[fast], slow = nums[slow]);
return nums[slow];
}
是不是简洁如斯!只要4行!达成人生理想!……算了只是个噱头,我们接下来会有一个正常的版本,首先让我我们条分缕析,从头说起。
图文详解
步骤1:数组即链表
通常链表的每个节点包含val(值)和next(指向下个节点)两部分。在本题目的场景下:
将第i个数x视为链表中的节点,指向第x个节点。
以一个例子贯穿始终。N=7,给定长度为8的数组nums=[6, 1, 4, 7, 3, 4, 2, 5]。则可以将它视为链表,如图:
由于数组长度为N+1,而所有数字都在[1, N],所以不会溢出。
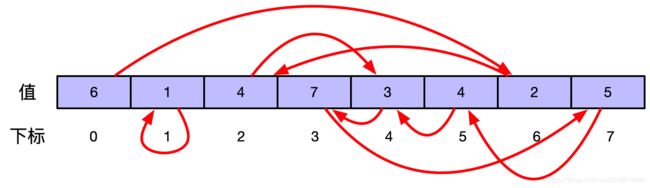
步骤2:重复即有环
上一步,我们将数组构造成了链表,或者说图。下面我们要理解“重复数字”和“环”的关系。
先写几条陈述:
- 每个数值代表一个指针,重复数字意味着有至少两个节点指向了同一个节点。
- 第i个数字
nums[i]==i,可以被视为一个自环。(如上图中的1) - 有环并不意味着有重复数字。例如
nums=[1,2,0],也构成了环,但没有重复数字。
非形式化证明:为什么一定有环
每个节点的next均不为空,且都指向[1, N]这个N个顶点。假设图中无环。任选一个节点,沿着指针跳N-1步之后,会发现[1,N]这N个节点都在这条链上(串成一串)。那么最新走到的节点会指向哪里呢?一定会指向链子上的某个节点。这就构成了环。矛盾。
所以一定有环。
非形式化证明:为什么一定有重复数字
我们早就用容斥原理得出了“一定有重复数字”,下面再用链表和环的思路佐证一下。两者殊途同归。
nums[0]是非常关键的节点。因为他没有父节点,或者说,没有节点指向他(自身位置为0,但所有指针数字都在[1,N])。从nums[0]出发,进入到 [1, N]这N个节点中,又已知这N个节点中一定有环,则nums[0]所在的连通图中一定包含这样的形状:一个环,外加一个孤支。如下图。像一个勺子,勺柄和勺子的连接处就一定有重复数字。
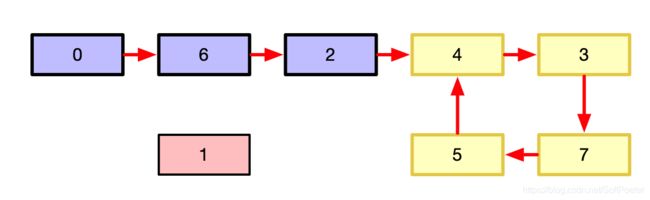
nums[0]的存在,让我们天然地站在了勺端。
解释太白话了,严格的数学证明也不难,但让我们暂时停在直觉理解阶段吧。
步骤3:找到重复数字
下面我们从nums[0]出发,寻找“连接处”。现在我么贴一下代码:
我们把代码写的正常一点:
public int findDuplicate(int[] nums) {
# P1
int slow = nums[0];
int fast = nums[slow];
# P2
while (slow != fast){
slow = nums[slow];
fast = nums[nums[fast]];
}
# P3
slow = 0;
# P4
while (slow != fast){
fast = nums[fast];
slow = nums[slow];
}
return slow;
}
算法包括四个步骤:
- 快指针和慢指针都从
nums[0]出发。运动速度是慢指针的两倍。 - 当slow=fast,意味着快指针追上了慢指针,显然,快慢指针都在环中了,否则不可能再次相遇。
- 此时将慢指针重回原点。
- 快慢指针以相同速度运动,最终会相会在“结合”处。
第四步有点奇妙吗?我们只要简单地做个计算即可。
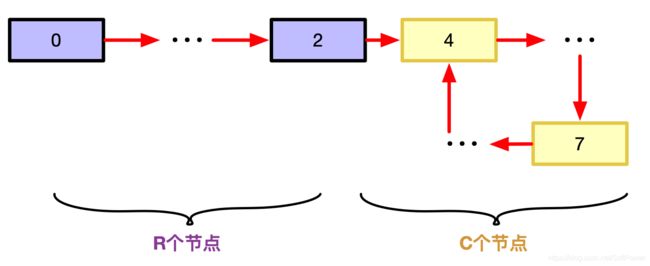
设孤立分支共 R R R个节点,环共 C C C个节点。
在第2步中:慢指针跳 x x x步,快指针跳 2 x 2x 2x步,快慢指针相会在环中,两者之间差n个整环:
2 x − x = n C x = n C 2x - x=nC\\ x = nC 2x−x=nCx=nC
在第4步中:慢指针从 0 0 0开始,快指针已经走了 2 n C 2nC 2nC步,此时两指针速度相同, R R R步之后慢指针到达结合处,此时快指针做了 2 n C + R 2nC+R 2nC+R步。意味着转了 2 n 2n 2n圈之后,又回到了结合处。
于是重复数字找到了。
快慢指针从本质上理解,可以视为构建了函数关系。这里是 x → 2 x x \rightarrow 2x x→2x,其他题目中可以是 x → 3 x + 1 x \rightarrow 3x+1 x→3x+1甚至是 x → x 2 x\rightarrow x^2 x→x2的关系。
从算法推原理是容易的,从头想可能会稍难一些。
复杂度分析
空间复杂度显然是 O ( 1 ) O(1) O(1).
时间复杂度上。主要看步骤2和步骤4.
步骤2. 的时间消耗为O(x),约束条件是:
x = n C x ≥ R 1 ≤ R < N , 1 ≤ C < N x=nC\\ x \geq R\\ 1 \leq R < N, 1 \leq C < N x=nCx≥R1≤R<N,1≤C<N
若要 x = n C ≥ N ≥ R x=nC\geq N \geq R x=nC≥N≥R,只需 x = ⌈ N / R ⌉ × R x=\lceil N/R \rceil \times R x=⌈N/R⌉×R.
此时有
x = ⌈ N R ⌉ × R x < ( N R + 1 ) × R = N + R < 2 N = O ( N ) x=\lceil \frac{N}{R} \rceil \times R \\ x < (\frac{N}{R} + 1) \times R = N + R < 2N = O(N) x=⌈RN⌉×Rx<(RN+1)×R=N+R<2N=O(N)
因此步骤2的复杂度是 O ( N ) O(N) O(N).
步骤四的复杂度自然是 O ( R ) < O ( N ) O(R) < O(N) O(R)<O(N),因此总体算法复杂度为 O ( N ) O(N) O(N).
结尾
除了“1~N的重复数字”的经典场景之外,还有很多变体,如1~N数组中第一个缺失的正数,以及任意范围数组中第一个缺失的正数等等,希望大家多多探索。