AtCoder题解 —— AtCoder Regular Contest 108 —— A - Sum and Product

题目相关

题目链接

AtCoder Regular Contest 108 A 题，https://atcoder.jp/contests/arc108/tasks/arc108_a。

Problem Statement

Given are integers S and P. Is there a pair of positive integers (N,M) such that N+M=S and N×M=P?

Input

Input is given from Standard Input in the following format:

S P

Output

If there is a pair of positive integers (N,M)(N,M) such that N+M=SN+M=S and N×M=PN×M=P, print Yes; otherwise, print No.

Samples1

Sample Input 1

3 2

Sample Output 1

Yes

Explaination

• For example, we have N+M=3 and N×M=2 for N=1,M=2.

Samples2

Sample Input 2

1000000000000 1

Sample Output 2

No

Constraints

• All values in input are integers.
• 

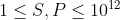
题解报告

题目翻译

给两个正整数 S, P，问是否存在正整数 N 和 M，满足 N+M=S 和 N*M=P。

题目分析

本题是一个比较简单的数学题。根据题目的要求，我们已知 S 和 P，问是否存在 N 和 M。这样，我们可以写出两个方程。

，这样就是一个二元一次方程组，只需要求解这个方程组即可。使用换元法，我们零 M=S-N，带入方程后得到，，利用左手法则，整理后我们得到一个一元二次方程，，这样可以通过韦达定理来求解方程的跟。

根据韦达定理，可知 ，即 。根据一元二次方程求根公式，我们知道：

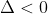• ，方程有两个虚数跟。本题不符合要求。
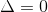• ，方程有两个相等整数跟。可能符合本题要求。
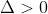• ，方程有两个不等的整数跟。可能符合本题要求。

根据一元二次方程求根公式，，根据题目提供的数据范围我们知道 b=-S，而 S>0，因此 b>0 的。因此当  等于零时候，方程有两个相等的正整数跟。当 ，题目要求有两个正整数跟，因此必须满足 ，也就是  即  才能有两个正整数跟。

数据范围估计

根据题目提供的数据范围 ，我们在计算中需要使用到平方，也就是说，最大的数据为 ，这说明超过了 unsigned long long 的范围。哪么怎么办？换一个更大的数据类型就可以了。最简单的方法就是讲所有数据当做 double 来处理，这样就可以解决问题。

总结

本题的难度不大，但是细节比较多。

AC 参考代码

//https://atcoder.jp/contests/arc108/tasks/arc108_a
//A - Sum and Product
#include 
#include 
using namespace std;
int main() {
    double s,p;
    cin>>s>>p;
    //n+m=s  m=s-n
    //n*m=p  n*(s-n)=p -n^2+s*n-p=0; n^2-s*n+p=0
    //需要有两个正整数跟，根据韦达定理, b^2-4ac，也就是
    //s*s-4*1*p=s*s+4*p>0
    double delta=s*s-4*p;
    if (delta<0) {
        //虚数根
        cout<<"No\n";
    } else if (0==delta) {
        //相同根
        cout<<"Yes\n";
    } else {
        //计算出根
        double x=(s+sqrt(delta))/2;
        double y=(s-sqrt(delta))/2;
        if (y>0 && x+y==s && x*y==p) {
            cout<<"Yes\n";
        } else {
            cout<<"No\n";
        }
    }

    return 0;
}

写代码的时候，用了比较笨的方法，直接将两个跟计算出来，进行比较。

时间复杂度

O(1)。

空间复杂度

O(1)。

枚举

首先感谢 T_a_r_j_a_n 的评论。本题确实可以换一个思路，就是从 1 到 sqrt(P) 中枚举，是否存在数据满足条件。为什么要开根号，因为我们有一个是乘积，N*M=P。

这里需要特别注意数据范围问题，最大数据为 1e12，超过了 int 可以表示范围，需要使用 long long 进行枚举。

而且使用枚举的方法，可以避免浮点数比较中头大的精度问题。

AC 参考代码

//https://atcoder.jp/contests/arc108/tasks/arc108_a
//A - Sum and Product
//从 1 到 sqrt(P) 中枚举是否存在 N 和 M。
#include 

using namespace std;

//如果提交到OJ，不要定义 __LOCAL
//#define __LOCAL

int main() {
#ifndef __LOCAL
    //这部分代码需要提交到OJ，本地调试不使用
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
#endif
    long long s,p;
    cin>>s>>p;

    long long t=sqrt(p);
    for (long long i=1; i<=t; i++) {
        long long n=i;
        long long m=s-i;
        if (n*m==p) {
            cout<<"Yes\n";
            return 0;
        }
    }
    cout<<"No\n";

#ifdef __LOCAL
    //这部分代码不需要提交到OJ，本地调试使用
    system("pause");
#endif
    return 0;
}

时间复杂度

，其实就是 。

空间复杂度

O(1)。