【前端算法系列】字符串
常用技能
- 反转字符串
str.split('').reverse().join('')
- 回文字符串(对称性和双指针)
- 反转完等于现状
- 可以从中间位置劈开,两边的子串在内容上完全对称
const len = str.length
// 遍历前半部分,判断和后半部分是否对称
for(let i=0; i<len/2; i++){
if(str[i]!==str[len-i-1]){
return false
}
}
- 字符串常用方法
- str.trim() 去掉空格
680.验证回文字符串 Ⅱ
给定一个非空字符串s,最多删除一个字符。判断是否能成为回文字符串
1)初始化两个指针,一个指向字符串头部,另一个指向尾部
2)如果两个指针所指的字符恰好相等,那么这两个字符就符合了回文字符串对对称性的要求,跳过它们往下走即可
3)如果不相等,意味着不对称发生了,可以删掉试试看,看看区间[left+1, right] 或 [left, right-1] 的字符串是否回文
如果是,就意味着删掉不回文的那个节点,整个字符串就是回文了
const validPalindrome = function(s) {
const len = s.length
// 左右指针
let i=0, j=len-1
// 当左右指针均满足对称时,一起向中间前进
while(i<j && s[i]===s[j]){
i++
j--
}
// 判断跳过左指针后字符串是否回文
if(isPalindrome(i+1, j)){
return true
}
// 判断跳过左指针后字符串是否回文
if(isPalindrome(i, j-1)){
return true
}
function isPalindrome(st, ed){
while(st<ed){
if(s[st]!==s[ed]){
return false
}
st++
ed--
}
return true
}
// 默认返回fasle
return false
}
console.log(validPalindrome('abddca'))
反转字符串中的单词 III
给定一个字符串,你需要反转字符串中每个单词的字符顺序,同时仍保留空格和单词的初始顺序
注意:在字符串中,每个单词由单个空格分隔,并且字符串中不会有任何额外的空格
示例 1:
输入: “Let’s take LeetCode contest”
输出: “s’teL ekat edoCteeL tsetnoc”
思路:把字符串split(’’)转成数组,借助数组的reverse反转后,用join(’’)转回字符串
const reverseWords=(arr)=>{
// 也可以用split(/\s/g) \s表示空格 split做分割 match去哪些识别
// 或者match(/[\w']+/g) []可选项 \W 字符 '为Let's的点
return arr.split(' ').map(item => {
return item.split('').reverse().join('')
}).join(' ')
}
const arr = "Let's take LeetCode contest"
console.log(reverseWords(arr))
match() 用于字符串, exec() 用于对象
211.添加与搜索单词-数据结构设计
既可以被添加,又可以被搜索,即会被存储起来,用Map(用对象字面量来模拟Map)
1)使用Map来存储值,使用字符串长度做key {3:['asd','fgh','jkl'], 4:['asdf']}
2)添加:如果已经存在相同的key,只做添加;不存在就创建
3)搜索:没有字符串长度的key表示不存在;
字符串不包含’.'为普通字符串;找到对应长度的数组,判断是否包含这个字符串
如果是正则,创建正则表达式对象,找到对应长度的数组,判断是否存在一个能够与正则相匹配
// 构造函数
const WordDictionary = function () {
// 初始化一个对象字面量,承担 Map 的角色
this.words = {}
console.log(this.words)
};
// 添加字符串的方法
WordDictionary.prototype.addWord = function (word) {
// 若该字符串对应长度的数组已经存在,则只做添加
if (this.words[word.length]) {
this.words[word.length].push(word)
} else {
// 若该字符串对应长度的数组还不存在,则先创建
this.words[word.length] = [word]
}
};
// 搜索方法
WordDictionary.prototype.search = function (word) {
// 若该字符串长度在 Map 中对应的数组根本不存在,则可判断该字符串不存在
if (!this.words[word.length]) {
return false
}
const len = word.length
// 如果字符串中不包含‘.’,那么一定是普通字符串
if (!word.includes('.')) {
// 定位到和目标字符串长度一致的字符串数组,在其中查找是否存在该字符串
return this.words[len].includes(word)
}
// 否则是正则表达式,要先创建正则表达式对象
const reg = new RegExp(word)
// 只要数组中有一个匹配正则表达式的字符串,就返回true
return this.words[len].some((item) => {
return reg.test(item)
})
};
const w = new WordDictionary()
w.addWord("bad")
w.addWord("dad")
w.addWord("mad")
w.addWord(/[0-9]+/)
// w.search("pad")
// w.search("bad")
// w.search(".ad")
console.log(w.search(/[0-9]+/))
8.字符串转换整数(atoi)
1)数值范围为[−2^31, 2^31 − 1],即max = Math.pow(2,31) - 1, min = -max - 1
2)使用match()捕获结果,把捕获的结果转成数字,看是否超出范围
const myAtoi = function(str) {
// 编写正则表达式
const reg = /\s*([-\+]?[0-9]*).*/
// 得到捕获组
const groups = str.match(reg)
// 计算最大值
const max = Math.pow(2,31) - 1
// 计算最小值
const min = -max - 1
// targetNum 用于存储转化出来的数字
let targetNum = 0
// 如果匹配成功
if(groups) {
// 尝试转化捕获到的结构
targetNum = +groups[1]
// 注意,即便成功,也可能出现非数字的情况,比如单一个'+'
if(isNaN(targetNum)) {
// 不能进行有效的转换时,请返回 0
targetNum = 0
}
}
// 卡口判断
if(targetNum > max) {
return max
} else if( targetNum < min) {
return min
}
// 返回转换结果
return targetNum
}
计数二进制子串
给定一个字符串s,计算具有相同数量0和1的非空(连续)子字符串的数量,并且这些子字符串中的所有0和所有1都是组合在一起的。
重复出现的子串要计算它们出现的次数。
输入: “00110011”
输出: 6
解释: 有6个子串具有相同数量的连续1和0:“0011”,“01”,“1100”,“10”,“0011” 和 “01”。
思路:光标向右移动(字符串长度确定的用for循环),找匹配的字符串(必须有1和0)
const countBinarySubstrings = (str) => {
// 建立数据结构,堆栈,保存数据
let r = []
// 给定任意子输入都返回第一个符合条件的子串
let match = (str) => {
let j = str.match(/^(0+|1+)/)[0] // () 匹配字符串
console.log('j------->'+j)
console.log('j[0]------->'+j[0] )
// ^:按位异或(相同为0,不同为1) 1%2 余数为1,所以1的二进制为1 0的二进制为0
// 作用:如果j是0,就位运算变为1;如果是1就位运算变为0,确保字符串有1和0
let o = (j[0] ^ 1).toString().repeat(j.length)
let reg = new RegExp(`^(${j}${o})`)
if (reg.test(str)) {
console.log(reg)
return RegExp.$1
} else {
return ''
}
}
// 1. 通过for循环控制程序运行的流程
for (let i = 0, len = str.length - 1; i < len; i++) {
// 2. 找到匹配的,只要有一个匹配的就push到r中
let sub = match(str.slice(i))
if (sub) {
r.push(sub)
}
}
return r
}
console.log(countBinarySubstrings("00110011")) // ["0011", "01", "1100", "10", "0011", "01"]
无重复字符的最长子串
给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度
输入: “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”,所以其长度为 3
思路:
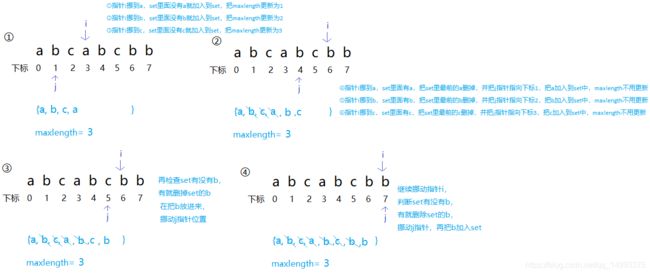
1)创建一个set,两个指针,指针j指向字符串靠头,指针i随着for循环遍历字符串
2)如果set没有str[i], 说明目前为止还没有重复的字符,把str[i]添加到set里,然后更新最大不重复字符的数量。
如果set没有str[i],则从set里前头开始删除str[i],并且递增j,再检查set里是否有str[i],如此反复直到set里没有str[i]为止
3)重复第二步,直到遍历完整个字符串
function lengthOfLongestSubstring(s) {
const set = new Set()
let i =0, j =0,maxLength=0;
if(s.length ===0) return 0
for(i; i<s.length;i++){
if(!set.has(s[i])){
set.add(s[i])
maxLength = Math.max(maxLength, set.size)
}else{
while(set.has(s[i])){
set.delete(s[j])
j++
}
set.add(s[i])
}
}
return maxLength
};
console.log(lengthOfLongestSubstring("pwwkew"))
交换星号
题目:一个字符串中只包含 * 和数字,请把 * 号都放开头。
思路:使用两个指针,从后往前扫字符串,遇到数字则赋值给后面的指针,继续往后扫,遇到 * 则不处理。
逆序操作数组,遇见数字则向后置,遍历完一遍后,所有的数字都已经在后边了,同时把前边的数组项用 * 填充
const isNumeric = n => !isNaN(parseFloat(n)) && isFinite(n);
const solution = s => {
const n = s.length
let a = s.split('')
let j = n - 1
for (let i = n - 1; i >= 0; --i){
if (isNumeric(a[i])) a[j--] = a[i] // 遍历,把数组中数字放回数组
}
//此时a = ["1", "3", "1", "3", "4", "2", "3", "2", "5", "4", "4"]
// 走到这步,j等于1 、0
for (; j >= 0; --j){
a[j] = '*'
}
return a.join('')
}
console.log(solution('134*232*544'))
替换、重复等,都可以优先考虑双指针
复原IP地址 (视频6)
ip地址规则:
- 分四段
- 每段都在0~255之间
- 每段之间用.区分
- 段内的数字如果是0则直接进入下一段,不存在01.02.03.04的ip
剪枝条件
- 剩余字符串需要小于剩余段*3
- 单段数字不可超过255
- 如果当段首字是0,则保留自身,进行递归
串联所有单词的子串
https://blog.csdn.net/qq_28410301/article/details/100521743
整数反转
- 先取符号 采用es6 Math.sign 符号函数, 正数返回 1 ,负数返回 -1
- 绝对值-> 转字符串 -> 字符串转数组 -> 反转数组 -> 字符串 -> 上符号 -> 判断范围
var reverse = function(x) {
let sign = Math.sign(x)
let res = (Math.abs(x) + '').split('').reverse().join('') * sign
if (res > Math.pow(2, 31) - 1 || res < Math.pow(2, 31) * -1) res = 0
return res
};
console.log(reverse(-321))
14. 最长公共前缀
1.暴力枚举
2.两层循环:把字符串对其排在一起检查,第一列是否相同,相同看第二列,不相同把前面的输出且停止
flower
flow
flight
for(let i=0;i<str[0].length;i++){
let c = str[0].chatAt(i)
for(let j=1;j<str.length;j++){
if(i==str[j].length || str[j].charAt(I)!=C){
return str[0].substring(0,i)
}
}
}
return str[0]
151.翻转字符串里的单词
1. split reverse join
2. reverse整个string,然后单独reverse每个单词
function reverseWords(s){
let word = s.trim().split(" +")
collenctions.reverse(A)
}
438
拥有长度为3的窗口,这个窗口从左边慢慢向右边滑动,每次滑动一步就看窗口里面的单词和p是不是异位词
最长回文子串
高级字符串算法
1143.最长公共子序列
子串和子序列的区别:子序列可以有间隔,子串没有
把text1和text2的长度暂存起来,初始化数组二维的初始值为0
-1表示删掉字符
dp[i][j] = dp[i-1][j-1]+1 if(s1[i-1]==s2[j-1])
else dp[i][j] = max(dp[i-1][j], dp[i][j-1])
最长子串
dp[i][j] = dp[i-1][j-1] +1 if(s1[i-1]==s2[j-1])
else dp[i][j]=0
72.编辑距离
dp[i][j] 代表word1到i位置转换成word2到j位置需要最少步数(word1的前i个字符 word2的前j个字符)
如果w1[i] == w2[j] 说明这两个字符串相同,就减少一个字符(因为被用了所以要减少)继续走下一个,于是 edit_dist(i, j) = edit_dist(i-1, j-1)
当 word1[i] == word2[j],dp[i][j] = dp[i-1][j-1];
当 word1[i] != word2[j],dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1
// edit_dist(i, j) = min(edit_dist(i-1, j-1)+1, edit_dist(i-1, j)+1, edit_dist(i, j-1)+1)
dp[i-1][j-1] 表示替换操作,
dp[i-1][j] 表示删除操作, word2 为空,需要的最少步数,就是删除操作
dp[i][j-1] 表示插入操作 word1 为空变成 word2 最少步数,就是插入操作
参考
5.最长回文子串
1. 暴力求解 O(n^3):嵌套循环,枚举i,j(起点和终点),判断该子串是否回文
let res = ''
let dp = new boolean[n][n]
for(let i=n-1; i>=0; i--){
for(let j=i; j<n; j++){
dp[i][j] = s.charAt(i) === s.chatAt(j) && (j-i)<2 || dp[i+1][j-1]
if(dp[i][j] && j-i+1 > res.length){
res = s.substring(i, j+1)
}
}
}
2.