力扣打卡day15
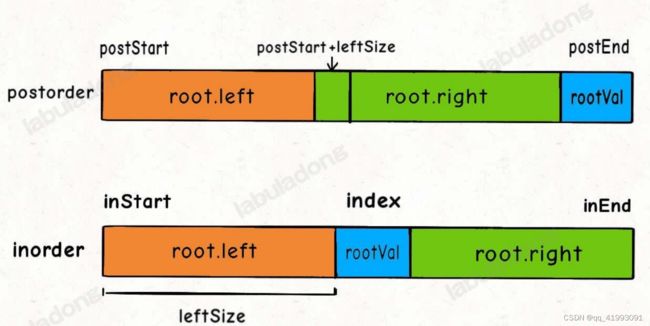
构造二叉树
class Solution {
HashMap<Integer,Integer> map=new HashMap<>();
public TreeNode buildTree(int[] inorder, int[] postorder) {
for(int i=0;i<inorder.length;i++){
map.put(inorder[i],i);
}
return build(inorder,0,inorder.length-1,postorder,0,postorder.length-1);
}
public TreeNode build(int[] inorder,int inStart,int inEnd,int[] postorder,int postStart,int postEnd){
if(inStart>inEnd){
return null;
}
int rootNode=postorder[postEnd];
//定义根节点
TreeNode root=new TreeNode(rootNode);
int index=map.get(rootNode);
//切中序数组
int leftSize=index-inStart;
root.left=build(inorder,inStart,index-1,postorder,postStart,postStart+leftSize-1);
root.right=build(inorder,index+1,inEnd,postorder,postStart+leftSize,postEnd-1);
return root;
}
}
105. 从前序与中序遍历序列构造二叉树
class Solution {
HashMap<Integer,Integer> map=new HashMap<>();
public TreeNode buildTree(int[] preorder, int[] inorder) {
for(int i=0;i<inorder.length;i++){
map.put(inorder[i],i);
}
return build(preorder,0,preorder.length-1,inorder,0,inorder.length-1);
}
public TreeNode build(int[] preorder,int preStart,int preEnd,int[] inorder,int inStart,int inEnd){
if(inStart>inEnd){
return null;
}
int rootNode=preorder[preStart];
//定义根节点
TreeNode root=new TreeNode(rootNode);
int index=map.get(rootNode);
//切中序数组
int leftSize=index-inStart;
root.left=build(preorder,preStart+1,preStart+leftSize,inorder,inStart,index-1);
root.right=build(preorder,preStart+leftSize+1,preEnd,inorder,index+1,inEnd);
return root;
}
}
654. 最大二叉树
class Solution {
public TreeNode constructMaximumBinaryTree(int[] nums) {
return build(nums,0,nums.length-1);
}
public TreeNode build(int[] nums,int l,int r){
if(l>r) return null;
int index=0;
int max=Integer.MIN_VALUE;
for(int i=l;i<=r;i++){
if(nums[i]>max){
max=nums[i];
index=i;
}
}
TreeNode root=new TreeNode(max);
root.left=build(nums,l,index-1);
root.right=build(nums,index+1,r);
return root;
}
}
617. 合并二叉树
方法一:在root1上进行合并
class Solution {
public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
//以下两步包含了root1和root2同时为空的情况
//终止条件
if(root1==null){
return root2;
}
if(root2==null){
return root1;
}
//直接改root1不建新的树
//root1和root2不为空的情况
root1.val+=root2.val;
root1.left=mergeTrees(root1.left,root2.left);
root1.right=mergeTrees(root1.right,root2.right);
return root1;
}
}
方法二:创建一个新的合并树
class Solution {
public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
//以下两步包含了root1和root2同时为空的情况
//终止条件
if(root1==null){
return root2;
}
if(root2==null){
return root1;
}
//若定义一个新的二叉树
TreeNode root=new TreeNode(0);
root.val=root1.val+root2.val;
root.left=mergeTrees(root1.left,root2.left);
root.right=mergeTrees(root1.right,root2.right);
return root;
}
}
二叉搜索树
二叉搜索树
二叉搜索树(BST)是一种特殊的二叉树,只需要记住两个特点
(1)左小右大,即每个节点的左子树都比当前结点的值小,右子树都比当前节点的值大
(2)中序遍历结果是有序的(升序)
700. 二叉搜索树中的搜索
方法一:递归法
class Solution {
public TreeNode searchBST(TreeNode root, int val) {
if(root==null||root.val==val) return root;
//存返回值
TreeNode res=new TreeNode(0);
if(val<root.val){
res=searchBST(root.left,val);
}
if(val>root.val){
res=searchBST(root.right,val);
}
return res;
}
}
方法二:迭代法
class Solution {
public TreeNode searchBST(TreeNode root, int val) {
while(root!=null){
if(root.val>val){
root=root.left;
}else if(root.val<val){
root=root.right;
}else{
return root;
}
}
return null;
}
}
98. 验证二叉搜索树
class Solution {
long max=Long.MIN_VALUE;
public boolean isValidBST(TreeNode root) {
if(root==null) return true;
//左子树是不是一个合法的二叉搜索树
boolean left=isValidBST(root.left);
//中
if(root.val>max){
max=root.val;
}else{
return false;
}
boolean right=isValidBST(root.right);
return left&&right;
}
}