2018SD省队集训R1 D3

T1

题解：

首先你可以写一个n=L的暴力，这样可以得到20pts
Polya定理的应用。先来看Polya定理。

Polya定理：设 G = {a1，a2，…，ag}是 N 个对象的置换群，用 M 种颜色给这 N 个对象着色，则不同的着色 方案数为：|G|^(-1) * {M^c(a1) + M^c(a2) + … + M^c(ag)}。

其中 c(ai)为置换 ai 的循环节数，( i = 1，2，…，g )。

对于这道题，直接用Polya定理求解，找出所有的置换，并求出置换的循环节数。然后根据上边公式求出 M^c(ai) 的总和，再除以置换群个数。

对于这个题目，用的是旋转置换，分别顺时针旋转 i 个珠子，其循环节长度为 LCM(N，i) / i，循环节数为N / (LCM(N，i) / i)，即 GCD(N，i)。

代码：

20pts

#include 
#include 
#define LL long long 
using namespace std;
const int mod=1e9+7;
const int N=1000005;
LL mul[N],inv[N];
LL ksm(LL a,LL k)
{
    LL ans=1;
    for (;k;k>>=1,a=a*a%mod)
      if (k&1) ans=ans*a%mod;
    return ans;
}
int gcd(int a,int b){if (!b) return a;else return gcd(b,a%b);}
int main()
{
    freopen("color.in","r",stdin);
    freopen("color.out","w",stdout);
    int n,k,l;scanf("%d%d%d",&n,&k,&l);
    if (n==l)
    {
        LL sum=0;
        for (int i=1;i<=n;i++) sum=(sum+ksm(k,gcd(n,i)))%mod;  
        sum=sum*ksm(n,mod-2)%mod;
        printf("%lld",sum);
    }
}

T2

题解：

挖坑待填

代码：

T3

题解：

这个题目考场上一眼暴力都不会写。。。那就从暴力说起吧
我们可以枚举每一个格子的上三角形先被消掉还是下面的三角形先被消掉，我们假设上面的三角先被删掉，可以建立一个依赖关系，像这样

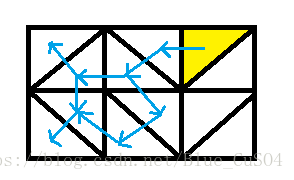
然后可以瞎搞计数，这样的复杂度是 O((rc)2)=O(r4) O ( ( r c ) 2 ) = O ( r 4 )

然后我们看看数据范围发现 O(r3) O ( r 3 ) 就能过了，优化并不是很多。

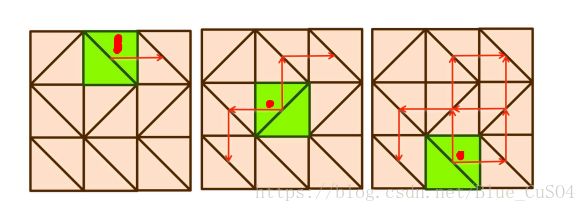
（画红点的是开始走的点）
如果格子上面的三角形要被删，那么肯定要先删格子[i-1][j]，从上面开始，记忆化搜索， O(r2c) O ( r 2 c )

代码：

#include 
#include 
#include 
#include 
#define rep(i,n) for (int i = 0; i < n; ++i)
using namespace std;
typedef vector<int> VI;
typedef vector VVI;

const int INF = 1001001001;
const int di[] = {-1,0,1,0}, dj[] = {0,-1,0,1}; //^

int h, w;
VVI used, dv;
int dfs(int i, int j, int v) {
  if (used[i][j] == 1) return INF;
  if (used[i][j] == 2) return 0;
  int res = 2;
  used[i][j] = 1;
  rep(k,2) {
    int nv = v^(dv[i][j]*k);
    int ni = i + di[nv], nj = j + dj[nv];
    if (ni < 0 || nj < 0 || ni >= h || nj >= w) continue;
    int r = dfs(ni,nj,nv);
    if (r == INF) return INF;
    res += r;
  }
  used[i][j] = 2;
  return res;
}

int main() {
    freopen("grid.in","r",stdin);
    freopen("grid.out","w",stdout);
  cin >> h >> w;
  vector<string> s(h);
  rep(i,h) cin >> s[i];
  dv = VVI(h, VI(w));
  rep(i,h)rep(j,w) dv[i][j] = (s[i][j] == 'Z') ? 1 : 3;
  VVI ans(h, VI(w, INF));
  rep(j,w)for (int v = 0; v <= 2; v += 2) {
    used = VVI(h, VI(w));
    int sum = 0;
    rep(i,h) {
      int si = i;
      if (v == 2) si = h-1-i;
      int res = dfs(si,j,v);
      if (res == INF) break;
      sum += res;
      ans[si][j] = min(ans[si][j], sum);
    }
  }
  rep(i,h)rep(j,w) if (ans[i][j] == INF) ans[i][j] = -1;
  rep(i,h)rep(j,w) printf("%d%c", ans[i][j], (j == w-1) ? '\n' : ' ');
  return 0;
}