数值实验3：插值法

插值法

1 实验目的

1. 熟悉拉格朗日插值多项式和牛顿插值多项式，注意其不同特点。
2. 观察高次插值的荣格现象。

2 实验内容

1） 已知函数表

实验1
x(i)	0.56160	0.56280	0.56401	0.56521
y(i)	0.82741	0.82659	0.82577	0.82495

用三次拉格朗日插值多项式求 x=0.5635 时的函数近似值。

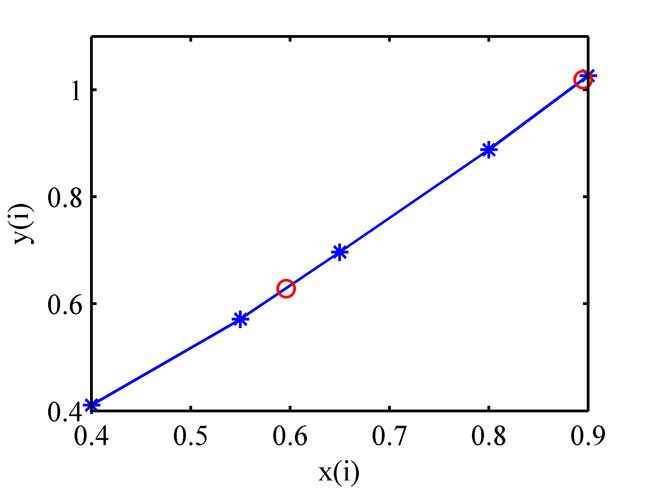
2） 已知函数表

实验2
x(i)	0.4	0.55	0.65	0.8	0.9
y(i)	0.41075	0.5715	0.69675	0.88811	1.02652

用牛顿插值多项式求 x=0.596 和 x=0.895 时的函数近似值。

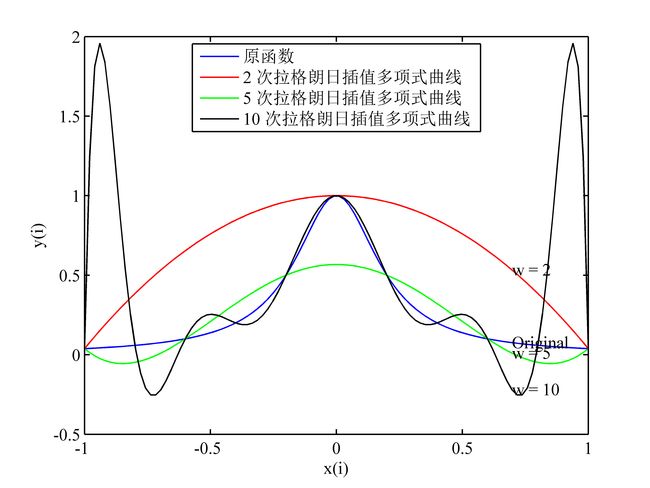
3）在区间 [−1,1] 上，分别构造函数 f(x) 的2次、5次和10次拉格朗日多项式，画出原函数和插值函数的图形，并将在节点数的函数值和插值多项式的函数值结果列表，观察并分析实验结果。其中函数 f(x) 为

f(x)=11+25x2

3 实验程序

实验程序主要包含拉格朗日插值和牛顿插值2个方法。

• 拉格朗日差值法

function [C, L] = Rlagranpoly(X, Y)
%拉格朗日插值 2015.11.18
% 调用格式：[C, L] = Rlagranpoly(X, Y)
% 输入：X = x 行向量
%       Y = y 行向量
% 输出：C = 多项式系数
%       L = 线性插值多项式
w = length(X);
n = w - 1;
L = zeros(w);
for k = 1 : n+1
    V = 1;
    for j = 1 : n+1
        if k ~= j
            V = conv(V, poly(X(j)))/(X(k)-X(j));
        end
    end
    L(k,:) = V;
end
C = Y*L;

• 牛顿插值法

function [C, D] = Rnewtonpoly(X, Y)
%牛顿插值 2015.11.18
% 调用格式：[C, D] = Rnewtonpoly(X, Y)
% 输入：X = x 行向量
%       Y = y 行向量
% 输出：C = 多项式系数
%       D = 差商表
n = length(X);
D = zeros(n);
D(:, 1) = Y';
for j = 2 : n
    for k = j : n
        D(k, j) = (D(k, j-1) - D(k-1, j-1))/(X(k) - X(k-j+1));
    end
end
C = D(n, n);
for k = n-1 : -1 : 1
    C = conv(C, poly(X(k)));
    m = length(C);
    C(m) = C(m) + D(k, k);
end

4 实验结果分析

4.1 实验一

问题1的解
x=0.5635	y=0.8261

4.2 实验二

问题2的解
x=0.596	y=0.6286
0.895	y=1.0191

4.3 实验三

• 2次拉格朗日插值多项式结果对比

xi	f(xi)	插值多项式函数值
−1	3.8462E−2	3.8462E−2
0	1	1
1	3.8462E−2	3.8462E−2

• 5次拉格朗日插值多项式结果对比

xi	f(xi)	插值多项式函数值
−1	3.8462E−2	3.8462E−2
-0.6	0.1	0.1
-0.2	0.5	0.5
0.2	0.5	0.5
0.6	0.1	0.1
1	3.8462E−2	3.8462E−2

• 10次拉格朗日插值多项式结果对比

xi	f(xi)	插值多项式函数值
−1	3.8462E−2	3.8462E−2
−0.8	5.8824E−2	5.8824E−2
−0.6	0.1	0.1000
−0.4	0.2	0.2000
−0.2	0.5	0.5000
0	1	1.000
0.2	0.5	0.5000
0.4	0.2	0.2000
0.6	0.1	0.1000
0.8	5.8824E−2	5.8824E−2
1	3.8462E−2	3.8462E−2

5 实验结论

本次实验研究了拉格朗日插值多项式和牛顿插值多项式的特性，并观察到了高次拉格朗日插值多项式在高阶插值的荣格现象。