模拟退火算法求解TSP问题（python）

模拟退火算法求解TSP的步骤参考书籍《Matlab智能算法30个案例分析》。

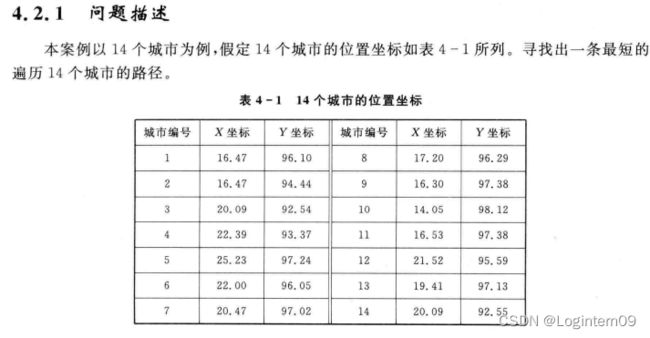
问题描述

TSP问题描述在该书籍的第4章

算法流程

部分实现代码片段

坐标轴转换成两点之间直线距离长度的代码

coordinates = np.array([(16.47, 96.10),
                            (16.47, 94.44),
                            (20.09, 92.54),
                            (22.39, 93.37),
                            (25.23, 97.24),
                            (22.00, 96.05),
                            (20.47, 97.02),
                            (17.20, 96.29),
                            (16.30, 97.38),
                            (14.05, 98.12),
                            (16.53, 97.38),
                            (21.52, 95.59),
                            (19.41, 97.13),
                            (20.09, 92.55),])

# 将距离坐标矩阵转换成两点之间实际的直线距离
city_num = coordinates.shape[0]


def get_distanceGraph(coordinates):
    # 计算城市间的欧式距离
    diatance_graph = np.zeros((city_num, city_num))
    # 初始化生成矩阵
    for i in range(city_num):
        for j in range(i, city_num):
            diatance_graph[i][j] = diatance_graph[j][i] = np.linalg.norm(coordinates[i] - coordinates[j])
    print("diatance_graph", diatance_graph)
    return diatance_graph

求解TSP问题路径长度的代码

def cal_length(cur_solution, distance_graph):
    # 计算路线长度
    total_length = 0
    visited_city_list = [cur_solution[0]]
    for i in range(city_num):
        visited_city = visited_city_list[-1]
        cur_city = cur_solution[i]
        visited_city_id = visited_city - 1
        cur_city_id = cur_city - 1
        next_city_length = distance_graph[visited_city_id][cur_city_id]
        total_length += next_city_length
        visited_city_list.append(cur_city)
    print("total_length", total_length)
    return total_length

使用一个路径长度矩阵相对简单，可以进行笔算验证解结果的算例，验证计算TSP路径长度的代码是可行的

可以笔算验证的算例代码

# 各个节点之间的欧氏距离
distance_list = [[0, 4.0, 6.0, 7.5, 9.0, 20.0, 10.0, 16.0, 8.0],
                [4.0, 0, 6.5, 4.0, 10.0, 5.0, 7.5, 11.0, 10.0],
                [6.0, 6.5, 0, 7.5, 10.0, 10.0, 7.5, 7.5, 7.5],
                [7.5, 4.0, 7.5, 0, 10.0, 5.0, 9.0, 9.0, 15.0],
                [9.0, 10.0, 10.0, 10.0, 0, 10.0, 7.5, 7.5, 10.0],
                [20.0, 5.0, 10.0, 5.0, 10.0, 0, 7.0, 9.0, 7.5],
                [10.0, 7.5, 7.5, 9.0, 7.5, 7.0, 0, 7.0, 10.0],
                [15.0, 11.0, 7.5, 9.0, 7.5, 9.0, 7.0, 0, 10.0],
                [8.0, 10.0, 7.5, 15.0, 10.0, 7.5, 10.0, 10.0, 0]]
demand_node_num = 9
supply_node_num = 0
city_num = 9
distance_graph = np.zeros((demand_node_num+supply_node_num, demand_node_num+supply_node_num))
for i in range(demand_node_num+supply_node_num):
    distance_graph[i] = np.array(distance_list[i])

cur_solution = [3, 9, 6, 4, 7, 8, 1, 5, 2]
length = cal_length(cur_solution, distance_graph)
print("length", length)

Metropolis准则函数

# Metropolis准则函数
def Metropolis_func(cur_solution, new_solution, distance_graph, cur_temp):
    # 计算新旧解之间的能量之差，如果能量降低：以概率1接受新解，如果能量升高，以一定概率接受劣化解
    dC = cal_length(new_solution, distance_graph) - cal_length(cur_solution, distance_graph)
    if dC < 0:
        cur_solution = new_solution
        cur_length = cal_length(cur_solution, distance_graph)
    elif pow(math.e, -dC/cur_temp) >= np.random.rand():  # 大于一个随机生成的数:
        cur_solution = new_solution
        cur_length = cal_length(cur_solution, distance_graph)
    else:
        cur_length = cal_length(cur_solution, distance_graph)
    return cur_solution, cur_length