冒泡排序及其优化
前言
本文将简单介绍冒泡排序及其优化版本,默认从小到大顺序
什么是冒泡排序
冒泡排序是一种简单且经典的排序算法。
基本思想: 是通过反复交换相邻的未按顺序排列的元素,将最小(或最大)的元素逐渐“浮”到正确位置。
时间复杂度: O(n^2)
排序稳定性: 稳定
说大白话就是两个位置判断是否符合小到大(大到小)顺序,不符合则交换,符合则下一轮,图例(一轮):
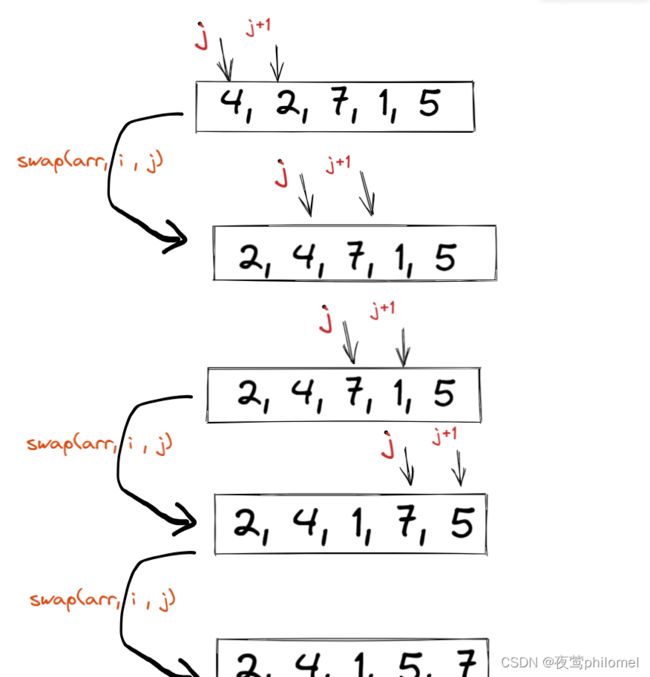
就上图所示,我们的数组{4,2,7,1,5},在交换排序这个过程中,需要两个指针进行辅助排序,两个指针是同时移动的,每移动一位就比较一次,这样就能将大的值往后放,小的值往前放,这样一轮下来,大的数是一定在被排序到数组往后位置的
既然一轮只能对部分数据进行排序,那么我们只需要多重复几次操作就可以了,次数 = arr.length - 1(2个数排序最多比较只需要1次,3个数排序最多比较需要2次)
public class BubbleSorted {
public static void main(String[] args) {
int[] arr = new int[]{4,2,7,1,5};
for(int i = 0; i < arr.length-1; i++){
for(int j = 0; j < arr.length - 1; j++){
if(arr[j] > arr[j+1]){
swap(arr, j, j+1);
}
}
}
for (int i : arr) {
System.out.println(i+" ");
}
}
private static void swap(int[] arr, int i, int j) {
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}
}
优化一
对于上面的这种冒泡排序每两两进行比较不管是否需要,这是一种比较耗时的操作,我们通过代码举个例子:
public class BubbleSorted {
public static void main(String[] args) {
int[] arr = new int[]{5, 8, 6, 1, 12, 13, 14};
for (int i = 0; i < arr.length - 1; i++) {
for (int j = 0; j < arr.length - 1; j++) {
if (arr[j] > arr[j + 1]) {
swap(arr, j, j + 1);
}
}
System.out.println("第"+(i+1)+"次排序结果:"+Arrays.toString(arr));
}
}
private static void swap(int[] arr, int i, int j) {
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}
}
运行结果:
第1次排序结果:[5, 6, 1, 8, 12, 13, 14]
第2次排序结果:[5, 1, 6, 8, 12, 13, 14]
第3次排序结果:[1, 5, 6, 8, 12, 13, 14]
第4次排序结果:[1, 5, 6, 8, 12, 13, 14]
第5次排序结果:[1, 5, 6, 8, 12, 13, 14]
第6次排序结果:[1, 5, 6, 8, 12, 13, 14]
我们不难发现,其实后面的456次排序是压根不需要了,因为它原本就是有序的,多余的判断是浪费时间的,那么我们要如何去判断后续已经有序不需要比较呢???
很简单,假如我们在一轮比较中,都没有需要进行交换,那么就意味着后面的顺序都是有序的,也就是说,我们第5次的排序结果可以通过第4次结果推导,如果有序则不再进行剩下的几轮排序,直接break,所以我们设置一个标记位即可,下面代码示例:
public class BubbleSorted {
public static void main(String[] args) {
int[] arr = new int[]{5, 8, 6, 1, 12, 13, 14};
for (int i = 0; i < arr.length - 1; i++) {
// 没一轮排序重置标记位,只有进入交换才说明本轮的排序结果可能任然是无序的,
//一次交换都没有进行,说明这一轮排序没有一个位置需要比较交换
boolean flag = true;
for (int j = 0; j < arr.length - 1; j++) {
if (arr[j] > arr[j + 1]) {
flag = false;
swap(arr, j, j + 1);
}
}
System.out.println("第"+(i+1)+"次排序结果:"+Arrays.toString(arr));
if(flag){
break;
}
}
}
private static void swap(int[] arr, int i, int j) {
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}
}
运行结果:
第1次排序结果:[5, 6, 1, 8, 12, 13, 14]
第2次排序结果:[5, 1, 6, 8, 12, 13, 14]
第3次排序结果:[1, 5, 6, 8, 12, 13, 14]
第4次排序结果:[1, 5, 6, 8, 12, 13, 14]
我们可以发现56轮已经不用再进行了,但是我们还需要第4轮来进行排序判断。
优化二
在优化一后,我们还可以对冒泡排序进行优化
首先,我们可以观察实例的结果,不难发现,每经过一轮排序,数组倒数位置上的数一定是有序的,因为每一轮的比较,大的数一定是往后跑的,那么就意味着,我们之后的比较排序不需要在对他们进行关注,所以我们每排序一次,内循环就少判断一位,以下是代码示例:
public static void main(String[] args) {
int[] arr = new int[]{5, 8, 6, 1, 12, 13, 14};
for (int i = 0; i < arr.length - 1; i++) {
boolean flag = true;
// 内循环循环次数每次 -i
for (int j = 0; j < arr.length - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
flag = false;
swap(arr, j, j + 1);
}
}
System.out.println("第"+(i+1)+"次排序结果:"+Arrays.toString(arr));
if(flag){
break;
}
}
}
private static void swap(int[] arr, int i, int j) {
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}
总结
冒泡排序是一种通过相邻两个数进行比较来进行排序的,可以通过两种优化的结合尽可能的提升效率,但是当数据量大的时候,效率依旧堪忧