2021全国大学生信息安全竞赛初赛部分Write up

全国大学生信息安全竞赛初赛部分Write up

纯队友做出来的就不写了，只写一下我参与解题的。(不会WEB，不会PWN，我打个锤子的ctf)

Misc

tiny traffic

流量题，直接过滤http包，在末尾发现两个GET请求，分别获取了test和secret的br包。

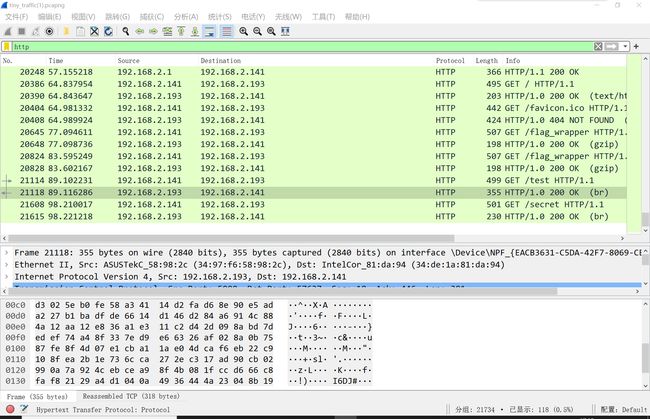
使用python对br包进行解压，发现test是proto3的源码，secret是一串字节型数据。

syntax = "proto3";

message PBResponse {
  int32 code = 1;
  int64 flag_part_convert_to_hex_plz = 2;
  message data {
    string junk_data = 2;
    string flag_part = 1;
  }
  repeated data dataList = 3;
  int32 flag_part_plz_convert_to_hex = 4;
  string flag_last_part = 5;
}

message PBRequest {
  string cate_id = 1;
  int32 page = 2;
  int32 pageSize = 3;
}

利用/test的源码可以对数据进行序列化，因此尝试对secret反序列化。

使用protobuf编译工具将/test的源码编译成python脚本。

./protoc.exe --python_out=. test.proto

生成test_pb2.py， 然后用python编写脚本反序列化secret，得到flag的五个部分，按要求进行拼接即可。

test = b'\x1b\x68\x01\x00\x1c\x07\x8e\xdb\x90\xdb\x43\xd4\x8f\x63\xd0\x96\xdb\xbc\x24\xed\x15\x2c\xd3\x02\x5e\xb0\xfe\x58\xa3\x41\x14\xd2\xfa\xd6\x8e\x90\xe5\xad\xa2\x27\xb1\xba\xdf\xde\x66\x14\xd1\x46\xd2\x84\xa6\x91\x4c\x88\x4a\x12\xaa\x12\xe8\x36\xa1\xe3\x11\xc2\xd4\x2d\x09\x8a\xbd\x7d\xed\xef\x74\xa4\x8f\x33\x7e\xd9\xe6\x63\x26\xaf\x02\x8a\x0b\x75\x87\xfe\x8f\x4d\x07\xe1\xcb\xa1\x1a\xe0\x4d\xca\xf6\xeb\x22\xc9\x10\x8f\xea\x2b\x1e\x73\x6c\xca\x27\x2e\xc3\x17\xad\x90\xcb\x02\x99\x0a\x7a\x92\x4c\xeb\xce\xa9\x8f\x4b\x08\x1f\xcc\xd6\x66\xc8\xfa\xf8\x21\x29\xa4\xd1\x04\x0a\x49\x36\x44\x4a\x23\x04\x8b\x19\x31\x33\x24\x8f\x38\x68\x37\x83\x09\xd9\xbc\x0b\x74\xa1\x2d\x7f\xde\x3d\x4f\x8f\x32\xb6\x85\x45\xc2\xe7\xd6\xc1\xa0\x17\x12\x0d\xf1\x73\x07'
secret = b'\x0b\x1c\x80\x08\xc8\x01\x10\xa2\xd4\x99\x07\x1a\x0e\x0a\x05\x65\x32\x33\x34\x35\x12\x05\x37\x61\x66\x32\x63\x1a\x0f\x0a\x06\x37\x38\x38\x39\x62\x30\x12\x05\x38\x32\x62\x63\x30\x20\xc6\xa2\xec\x07\x2a\x09\x64\x31\x37\x32\x61\x33\x38\x64\x63\x03'

import brotli
import test_pb2
# test = brotli.decompress(test).decode('utf-8')
# print(test)
secret = brotli.decompress(secret)
target = test_pb2.PBResponse()
target.ParseFromString(secret)
print(target)
flag = hex(target.flag_part_convert_to_hex_plz)[2:] + target.dataList[0].flag_part + target.dataList[1].flag_part + hex(target.flag_part_plz_convert_to_hex)[2:] + target.flag_last_part
print('CISCN{%s}' %flag)

running_pixel

gif隐写，第一步是分离每一帧，使用kali上的convert命令：

convert running_pixel.gif running_pixel.png

得到382帧图像，仔细查看，发现有些图像中有极小的白点。

使用画图提取小白点的位置和像素，像素值为(233,233,233)。发现临近的帧在临近的位置有相同像素的小白点。使用python脚本提取所有帧中的位置，并按照顺序重新绘图。

from PIL import Image

pix_t = []
pix_s = []
# 获取所有异常像素点
for k in range(382):
    fname = './in/running_pixel-'+str(k)+'.png'
    img = Image.open(fname)
    img = img.convert("RGB")
    for i in range(400):
        for j in range(400):
            tmp = img.getpixel((i,j))
            if tmp == (233,233,233):
                pix_t.append([i,j])
# print(pix_t)      

# 将异常像素点按顺序按字符分组绘图并放大
def create_letter(pixel, path):
    img = Image.new("RGB", [15,15], 'white')
    pix = img.load()
    l0, l1 = pix_t[start][0]-5, pix_t[start][1]-5
    for each in pixel:
        pix[each[1]-l1, each[0]-l0] = 1
    img = img.resize((75, 75), Image.ANTIALIAS)
    img.save('./out/'+str(path)+'.png')

start = 0
name = 0
for i in range(1, len(pix_t)):
    if abs(pix_t[i][0]-pix_t[i-1][0])>=2 and abs(pix_t[i][1]-pix_t[i-1][1])>=2:
        create_letter(pix_t[start:i], name)
        name += 1
        start = i
create_letter(pix_t[start:], name)

最后画出来的异常像素如下图所示：

Crypto

rsa

分析源码，三段rsa加密破解分别满足小公钥指数攻击、共模攻击和已知高位攻击。原理有一点点复杂，但是好在都给了实现的代码，改一改就能用。

对于已知高位攻击，使用sage是最方便的，如果没有装，可以使用在线版。

from sage.all import *
import binascii
n = 113432930155033263769270712825121761080813952100666693606866355917116416984149165507231925180593860836255402950358327422447359200689537217528547623691586008952619063846801829802637448874451228957635707553980210685985215887107300416969549087293746310593988908287181025770739538992559714587375763131132963783147
p4 = 7117286695925472918001071846973900342640107770214858928188419765628151478620236042882657992902
cipher = 59213696442373765895948702611659756779813897653022080905635545636905434038306468935283962686059037461940227618715695875589055593696352594630107082714757036815875497138523738695066811985036315624927897081153190329636864005133757096991035607918106529151451834369442313673849563635248465014289409374291381429646
e = 65537
pbits = 512
kbits = pbits - p4.nbits()
p4 = p4 << kbits
PR.<x> = PolynomialRing(Zmod(n))
f = x + p4
roots = f.small_roots(X=2^kbits, beta=0.4)
if roots:
    p = p4 + int(roots[0])
    assert n % p == 0
    q = n/int(p)
    phin = (p-1)*(q-1)
    d = inverse_mod(e,phin)
    flag = hex(int(pow(cipher,d,n)))[2:]
    print(binascii.unhexlify(flag))
    # b'nd black, and pale, and hectic red,\nPestilence-stricken multitudes: O thou,\nWho chariotest to their dark wintry bed\n'

其他两部分python就可以实现

import md5
from gmpy2 import *

n1 = 123814470394550598363280518848914546938137731026777975885846733672494493975703069760053867471836249473290828799962586855892685902902050630018312939010564945676699712246249820341712155938398068732866646422826619477180434858148938235662092482058999079105450136181685141895955574548671667320167741641072330259009
e1 = 3
c1 = 19105765285510667553313898813498220212421177527647187802549913914263968945493144633390670605116251064550364704789358830072133349108808799075021540479815182657667763617178044110939458834654922540704196330451979349353031578518479199454480458137984734402248011464467312753683234543319955893

n2 = 111381961169589927896512557754289420474877632607334685306667977794938824018345795836303161492076539375959731633270626091498843936401996648820451019811592594528673182109109991384472979198906744569181673282663323892346854520052840694924830064546269187849702880332522636682366270177489467478933966884097824069977
e2 = 17
e3 = 65537
c2 = 54995751387258798791895413216172284653407054079765769704170763023830130981480272943338445245689293729308200574217959018462512790523622252479258419498858307898118907076773470253533344877959508766285730509067829684427375759345623701605997067135659404296663877453758701010726561824951602615501078818914410959610
c3 = 91290935267458356541959327381220067466104890455391103989639822855753797805354139741959957951983943146108552762756444475545250343766798220348240377590112854890482375744876016191773471853704014735936608436210153669829454288199838827646402742554134017280213707222338496271289894681312606239512924842845268366950
c3 = invert(c3, n2) 

n3 = 113432930155033263769270712825121761080813952100666693606866355917116416984149165507231925180593860836255402950358327422447359200689537217528547623691586008952619063846801829802637448874451228957635707553980210685985215887107300416969549087293746310593988908287181025770739538992559714587375763131132963783147
c4 = 59213696442373765895948702611659756779813897653022080905635545636905434038306468935283962686059037461940227618715695875589055593696352594630107082714757036815875497138523738695066811985036315624927897081153190329636864005133757096991035607918106529151451834369442313673849563635248465014289409374291381429646
p4 = 7117286695925472918001071846973900342640107770214858928188419765628151478620236042882657992902

def get_m1():
    inputs = range(0, 100)
    for i in inputs:
        a, b = iroot(c1 + i * n1, 3)
        if b == 1:
            return '{:x}'.format(int(a)).decode('hex')

def get_m2():
    s = gcdext(e2, e3)
    s1 = s[1]
    s2 = -s[2]
    m = (pow(c2,s1,n2) * pow(c3 , s2 , n2)) % n2
    return '{:x}'.format(int(m)).decode('hex')

def get_m3():
    return b'nd black, and pale, and hectic red,\nPestilence-stricken multitudes: O thou,\nWho chariotest to their dark wintry bed\n'

if __name__ == '__main__':
    m1 = get_m1()
    m2 = get_m2()
    m3 = get_m3()
    m = m1+m2+m3
    print m
    print md5.new(m).hexdigest()

homo

从标题看是个同态加密，不过我也没看懂加密的过程。直接看代码吧。

task脚本开始运行后，首先要选择模式：game和decrypt。一开始是无法选择decrypt的，因为有一个全局变量allowed，只有game中猜对200次数字，allowed才能变成True，进入decrypt。

def game():
    global allowed
    count = 0
    random.seed(os.urandom(32))
    print("play a game with me!")
    for i in range(512):
        number = random.getrandbits(64)
        guess = int(input("your number:"))
        if guess == number:
            count += 1
            print("win")
        else:
            print(f"lose!my number is {number}\n")
    
    if count >= 200:
        allowed = True

这里每轮的number由random.getrandbits(64)产生，似乎是一个随机数。但是百度一下，发现这个函数使用了MT19937伪随机算法，该算法很早之前已经被破解，只需要得到624个连续的random.getrandbits(32)值就可预测一个值。这道题里是用64生成的，但实际上，getrandbits(64)是由两个getrandbits(32)生成的。

R1 = random.getrandbits(32)
R2 = random.getrandbits(32)
random.getrandbits(64) == (R2 << 32) + R1

因此312个随机数即可获得624个状态，旋转状态后即可预测之后的随机数。循环进行512次，正好在最后一轮循环得到200个正确的随机数。

至于加密函数的具体破解，我就没有看懂了，但是找到了一篇360前两年的论文Danger of using fully homomorphic encryption: A look at Microsoft SEAL，描述了三种攻击全同态加密的方式，并在github上给出了sage实现的源码，与本题密切相关的是CCA_attack_on_FPSI.py，实现上使用了sage内置的环，和题中的代码有一定区别，需要适当改写一下。

完整的解题脚本如下，其中需要注意的是，task.py要适当修改一下，把主函数用if __name__ == '__main__':包起来，不然在import时会直接执行task中的代码。

import os
import re
import random
from pwn import *
from poly import *
from math import floor
from task import Round, decrypt, q, n, t, T, delta

def invert_right(m,l,val=''):
    length = 32
    mx = 0xffffffff
    if val == '':
        val = mx
    i,res = 0,0
    while i*l<length:
        mask = (mx<<(length-l)&mx)>>i*l
        tmp = m & mask
        m = m^tmp>>l&val
        res += tmp
        i += 1
    return res

def invert_left(m,l,val):
    length = 32
    mx = 0xffffffff
    i,res = 0,0
    while i*l < length:
        mask = (mx>>(length-l)&mx)<<i*l
        tmp = m & mask
        m ^= tmp<<l&val
        res |= tmp
        i += 1
    return res

def invert_temper(m):
    m = invert_right(m,18)
    m = invert_left(m,15,4022730752)
    m = invert_left(m,7,2636928640)
    m = invert_right(m,11)
    return m

def clone_mt(record):
    state = [invert_temper(i) for i in record]
    gen = random.Random()
    gen.setstate((3,tuple(state+[0]),None))
    return gen

def get_random32(n):
    r1 = int(bin(n)[-32:],2)
    r2 = int(bin(n)[2:-32],2)
    return r1, r2

def get_random64(r1, r2):
    return (r2<<32)+r1

def crack_game(li):
    newnum = []
    res    = []
    prng   = []
    for i in range(312):
        r1, r2 = get_random32(li[i])
        prng.append(r1)
        prng.append(r2)

    g = clone_mt(prng)
    for i in range(624):
        g.getrandbits(32)

    for i in range(400):
        newnum.append(g.getrandbits(32))

    for i in range(200):
        res.append(get_random64(newnum[2*i], newnum[2*i+1]))

    return res

def recvline1():
    return sh.recvline()

def sendline1(data):
    sh.sendline(data)

def recc(sh, pattern='my number is '):
    data = recvline1().decode('utf-8')
    recvline1()
    if pattern:
        pattern += '(.*)'
        return int(re.search(pattern, data).group(1))

sh = remote("121.36.33.191","23434")
for i in range(313):
    sendline1(b'1')

pk_0 = eval(recvline1().decode('utf-8')[:-1])
pk_1 = eval(recvline1().decode('utf-8')[:-1])
ct_0 = eval(recvline1().decode('utf-8')[:-1])
ct_1 = eval(recvline1().decode('utf-8')[:-1])

for i in range(5):
    recvline1()

pr = []
for i in range(312):
    pr.append(recc(sh))

res = crack_game(pr)
for i in range(200):
    sendline1(str(res[i]).encode('utf-8'))

for i in range(200):
    recvline1()

def recover_key(pk0,pk1,i):
    t1    = [0 for _ in range(n)]
    t1[i] = M
    t2    = M
    t     = Poly(n, q)
    t.cofficient = t1
    cc0 = Round(pk0 + t,q)
    cc1 = Round(pk1 + t2,q)
    c0 = str(cc0.cofficient)[1:-1].replace(" ", "").encode('utf-8')
    c1 = str(cc1.cofficient)[1:-1].replace(" ", "").encode('utf-8')
    for j in range(4):
        recvline1()
    sendline1(b'2')
    sendline1(c0)
    sendline1(c1)
    recvline1()
    recvline1()
    s = eval(recvline1().decode('utf-8')[:-1])
    return s[i]

pk0 = Poly(n, q)
pk0.cofficient = pk_0
pk1 = Poly(n, q)
pk1.cofficient = pk_1
M = delta//4+50
Recoverd_key = []
for i in range(n):
    Recoverd_key.append(recover_key(pk0,pk1,i))

# print(Recoverd_key)
# print(ct_0)
# print(ct_1)

ct0 = Poly(n, q)
ct0.cofficient = ct_0
ct1 = Poly(n, q)
ct1.cofficient = ct_1
sk  = Poly(n, q)
sk.cofficient = Recoverd_key

tmp = decrypt(sk, [ct0, ct1]).cofficient
tmp = ''.join(map(str,tmp))
tmp = re.findall('.{8}', tmp)

flag = ''.join([chr(int(x,2)) for x in tmp])
print(flag)

Reverse

glass

拖到jadx里反编译一下，MainActivity代码中包含checkFlag函数，但是是包含在native-lib中的。

public class MainActivity extends AppCompatActivity {
    Button but;
    EditText txt;

    public native boolean checkFlag(String str);

    static {
        System.loadLibrary("native-lib");
    }

    /* Access modifiers changed, original: protected */
    public void onCreate(Bundle bundle) {
        super.onCreate(bundle);
        setContentView((int) R.layout.activity_main);
        this.but = (Button) findViewById(R.id.button);
        this.txt = (EditText) findViewById(R.id.editText);
        this.but.setOnClickListener(new OnClickListener() {
            public void onClick(View view) {
                MainActivity mainActivity = MainActivity.this;
                if (mainActivity.checkFlag(mainActivity.txt.getText().toString())) {
                    Toast.makeText(MainActivity.this, "right!", 0).show();
                } else {
                    Toast.makeText(MainActivity.this, "wrong!", 0).show();
                }
            }
        });
    }
}

用IDA打开libnative-lib.so找到checkFlag函数。首先判断输入长度为39，然后设置一个key为’12345678’，接下来两个函数点进去是明显的rc4，就不用细分析了。第三个函数是一个简单的分组加密，直接写脚本逆就行了。

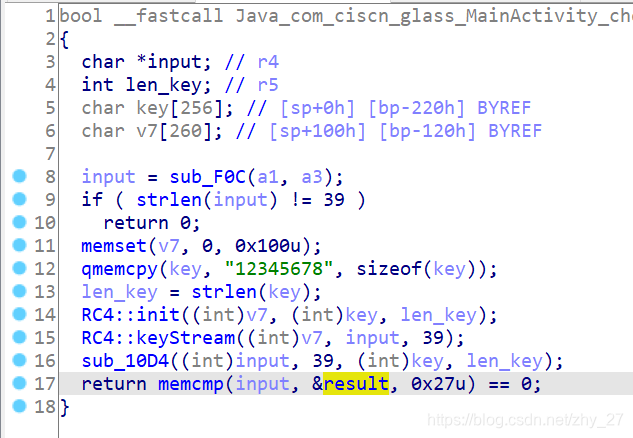
def re_sub10D4():
    key = b'12345678'
    res = [0xA3,  0x1A,  0xE3,  0x69, 0x2F,  0xBB,  0x1A,  0x84,  0x65,  0xC2,  0xAD,  0xAD,  0x9E,  0x96,  0x05,  0x02,  0x1F,  0x8E,  0x36,  0x4F, 0xE1,  0xEB,  0xAF,  0xF0,  0xEA,  0xC4,  0xA8,  0x2D, 0x42,  0xC7,  0x6E,  0x3F,  0xB0,  0xD3,  0xCC,  0x78, 0xF9,  0x98,  0x3F]
    for j in range(0, 39, 8):
        for k in range(8):
            if j+k >=39:
                break
            res[j+k] ^= key[k]
    for i in range(0, 39, 3):
        res[i+1] ^= res[i]
        res[i+2] ^= res[i+1]
        res[i]   ^= res[i+2]
    return res

from Crypto.Cipher import ARC4 as rc4
key = b'12345678'
enc = rc4.new(key)
data = bytearray(re_sub10D4())
res = enc.decrypt(data)
print(res)

baby_bc

给的是.bc文件，是llvm的中间件，在kali下可使用lli baby.bc执行，但为了反编译，先用clang编译至可执行文件然后用IDA查看。

clang baby.bc -o baby

IDA打开查看main函数。第一个判断是输入长度为25，且每一个值都小于等于5。

然后查看fill_number函数。

__int64 __fastcall fill_number(__int64 a1)
{
  v10 = 0LL;
  do
  {
    v9 = v10;
    v8 = 5 * v10;
    v7 = *(_BYTE *)(a1 + 5 * v10);
    if ( map[5 * v10] )
    {
      v6 = 0;
      if ( v7 != 48 )
        return v6 & 1;
    }
    else
    {
      map[5 * v10] = v7 - 48;
    }
    v5 = *(_BYTE *)(a1 + v8 + 1);
    if ( map[5 * v10 + 1] )
    {
      v6 = 0;
      if ( v5 != 48 )
        return v6 & 1;
    }
    else
    {
      map[5 * v10 + 1] = v5 - 48;
    }
    // ···
  while ( v9 + 1 < 5 );
  return v6 & 1;
}

逻辑还是很简单的，定义了一个5*5的map数组，检查每一个值是否已经被赋值（或者说是否为0）。如果map[i]不为0，则判断input[i]是否为字符’0’，如果是，返回失败。如果map[i]为0，就将input[i]-0x30赋值给map[i]，也就是从字符’12345’变为内存中的12345。

0000000000405050 00 00 00 00 00 00 00 00 00 00 00 00 04 00 00 00 …
0000000000405060 00 00 03 00 00 00 00 00 00 00 00 00 00 00 00 00 …

内存中map从0x405050地址开始，长度为25。其中只有两个元素不为0，也就是对应位置的输入应该是0。表示成5*5就是map[2][2]=4，map[3][3]=3。

然后查看docheck函数，很长，但是和fill_number函数很相似的是，存在大量语义相近的语句，实际核心代码就几句。

__int64 docheck()
{
  v12 = 0LL;
  do
  {
    v10 = v12;
    memset(v14, 0, sizeof(v14));
    v9 = &v14[(unsigned __int8)map[5 * v12]];
    if ( *v9
      || (*v9 = 1, v14[(unsigned __int8)map[5 * v12 + 1]])
      || (v14[(unsigned __int8)map[5 * v12 + 1]] = 1, v14[(unsigned __int8)map[5 * v12 + 2]])
      || (v14[(unsigned __int8)map[5 * v12 + 2]] = 1, v14[(unsigned __int8)map[5 * v12 + 3]])
      || (v14[(unsigned __int8)map[5 * v12 + 3]] = 1, v14[(unsigned __int8)map[5 * v12 + 4]]) )
    {
      v8 = 0;
      return v8 & 1;
    }
    ++v12;
  }
  while ( v10 + 1 < 5 );
  v11 = 0LL;
  while ( 1 )
  {
    v7 = v11;
    memset(v13, 0, sizeof(v13));
    v6 = &v13[(unsigned __int8)map[v11]];
    if ( *v6 )
      break;
    *v6 = 1;
    if ( v13[(unsigned __int8)byte_405055[v11]] )
      break;
    v13[(unsigned __int8)byte_405055[v11]] = 1;
    if ( v13[(unsigned __int8)byte_40505A[v11]] )
      break;
    v13[(unsigned __int8)byte_40505A[v11]] = 1;
    if ( v13[(unsigned __int8)byte_40505F[v11]] )
      break;
    v13[(unsigned __int8)byte_40505F[v11]] = 1;
    if ( v13[(unsigned __int8)byte_405064[v11]] )
      break;
    ++v11;
    if ( v7 + 1 >= 5 )
    {
      v5 = 0LL;
      while ( 1 )
      {
        v4 = v5;
        if ( row[4 * v5] == 1 )
        {
          if ( (unsigned __int8)map[5 * v5] < (unsigned __int8)map[5 * v5 + 1] )
            goto LABEL_27;
        }
        else if ( row[4 * v5] == 2 && (unsigned __int8)map[5 * v5] > (unsigned __int8)map[5 * v5 + 1] )
        {
LABEL_27:
          v8 = 0;
          return v8 & 1;
        }
        // ···
        ++v5;
        if ( v4 + 1 >= 5 )
        {
          v3 = 0LL;
          while ( 1 )
          {
            v2 = v3 + 1;
            if ( col[5 * v3] == 1 )
            {
              v1 = 0;
              if ( (unsigned __int8)map[5 * v3] > (unsigned __int8)map[5 * v2] )
                goto LABEL_26;
            }
            else if ( col[5 * v3] == 2 )
            {
              v1 = 0;
              if ( (unsigned __int8)map[5 * v3] < (unsigned __int8)map[5 * v2] )
              {
LABEL_26:
                v8 = v1;
                return v8 & 1;
              }
            }
            // ···
            ++v3;
            v1 = 1;
            if ( v2 >= 4 )
              goto LABEL_26;
          }
        }
      }
    }
  }
  v8 = 0;
  return v8 & 1;
}

第一个do while循环里是在判断map矩阵的每行不能有相同的数值，第二个大循环内前几行是判断矩阵的每列不能有相同元素。简单说，就是要求map是一个拉丁方矩阵。然后第二个大循环里LABEL_27附近的代码是根据row数组为矩阵行内设置限制条件，LABEL_26附近的代码是根据col数组为矩阵列内设置限制条件。如果row为1，则矩阵某行的某一个元素不能小于后一个元素，如果为2，就是不能大于某一个元素。列类似。

0000000000405070 00 00 00 01 01 00 00 00 02 00 00 01 00 00 00 00 …
0000000000405080 01 00 01 00 00 00 00 00 00 00 00 00 00 00 00 00 …
0000000000405090 00 00 02 00 02 00 00 00 00 00 00 00 00 01 00 00 …
00000000004050A0 01 00 00 01 ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? …???

内存中row从0x405070到0x405083，col从0x405090到0x4050a3，长度均为20。根据数值，可以写出该拉丁方矩阵的完整限制条件：

bool check2()
{
    if (map[0][3] < map[0][4]) return no;
    if (map[1][0] < map[1][1]) return no;
    if (map[2][0] > map[2][1]) return no;
    if (map[2][3] < map[2][4]) return no;
    if (map[4][0] < map[4][1]) return no;
    if (map[4][2] < map[4][3]) return no;

    if (map[0][2] < map[1][2]) return no;
    if (map[0][4] < map[1][4]) return no;
    if (map[2][3] > map[3][3]) return no;
    if (map[3][1] > map[4][1]) return no;
    if (map[3][4] > map[4][4]) return no;
    if (map[2][2] != 4) return no;
    if (map[3][3] != 3) return no;
    return ok;
}

然后在网上抄了个拉丁方的脚本，输出最后的矩阵：

#include 
#include 

int map[10][10], N = 5, count = 0;

bool check(int x,int y);
bool check2();
void make(int x,int y);
void print();

int main(){
    make(0,0);
    return 0;
}

bool check(int x,int y){
    int i;
    int checknum = map[x][y];
    for(i=0; i<y; i++)
        if(checknum == map[x][i]) return 0;
    for(i=0; i<x; i++)
        if(checknum == map[i][y]) return 0;
    return 1;
}

bool check2()
{
    if (map[0][3] < map[0][4]) return 0;
    if (map[1][0] < map[1][1]) return 0;
    if (map[2][0] > map[2][1]) return 0;
    if (map[2][3] < map[2][4]) return 0;
    if (map[4][0] < map[4][1]) return 0;
    if (map[4][2] < map[4][3]) return 0;

    if (map[0][2] < map[1][2]) return 0;
    if (map[0][4] < map[1][4]) return 0;
    if (map[2][3] > map[3][3]) return 0;
    if (map[3][1] > map[4][1]) return 0;
    if (map[3][4] > map[4][4]) return 0;
    if (map[2][2] != 4) return 0;
    if (map[3][3] != 3) return 0;
    return 1;
}

void make(int x,int y){
    if(count == N*N){
        if (check2()) print();
    }
    else{
        for(int i=1; i<=N; ++i){
            map[x][y] = i;
            count++;
            if(check(x,y)){
                int yy = (y+1)%N;
                int xx = x;
                if(y == N-1) xx =x+1;
                make(xx,yy);
            }
            --count;
            }
        }
}

void print(){
    for(int i=0; i<N; i++){
        for(int j=0; j<N; j++)
            printf("%2d",map[i][j]);
        printf("\n");
}
printf("\n");
}

输出的拉丁方矩阵为

1 4 2 5 3
5 3 1 4 2
3 5 4 2 1
2 1 5 3 4
4 2 3 1 5

将第三行的4和第四行的3换成0，即为所求输入。