【Acwing提高】并查集

【Acwing提高】并查集

知识点

题目	知识点
格子游戏	并查集判环
搭配购买	并查集维护集合大小+01背包
程序自动分析	并查集判冲突+离散化
银河英雄传说	并查集维护距离，边带权
奇偶游戏	离散化，奇偶转换，边带权/扩展域

题目

格子游戏

思路
裸的并查集不用维护什么东西，点与点成环游戏结束，即构建关系的时候在同一集合里。
这里有个技巧，并查集维护一个数比较方便，所以把二维坐标利用x*n+y转化成二维的（注意要让输入也自减，保证从0开始）
代码

#include
using namespace std;
const int N=4e4+10;
int n,m;
int p[N];

int get(int x,int y)
{
    return x*n+y;
}
int find(int x)
{
    if(p[x]!=x)p[x]=find(p[x]);
    return p[x];
}
int main()
{
    cin>>n>>m;
    for(int i=0;i<n*n;i++)p[i]=i;
    
    int res=0;
    for(int i=1;i<=m;i++)
    {
        int x,y;
        char d;
        cin>>x>>y>>d;
        x--;y--;
        int a=get(x,y);
        int b;
        if(d=='D')b=get(x+1,y);
        else b=get(x,y+1);
        
        int pa=find(a),pb=find(b);
        if(pa==pb)
        {
            res=i;
            break;
        }
        p[pa]=pb;
    }
    if(!res)puts("draw");
    else cout<<res<<endl;
    
    return 0;
}

搭配购买

思路
由于是无向图的关系（并查集主要处理无向图，有向图难搞（传递闭包））所以可以直接把连通块作为物品，可以对比一下有依赖的背包

先把有边相连的放到一个集合，把每个连通块作为一个物品做01背包

并查集要维护集合价值和体积的总和（绑定到祖宗节点上）
代码

#include
using namespace std;

const int N=1e5+10;
int n,m,vol;
int v[N],w[N];
int p[N];
int f[N];
int find(int x)
{
    if(p[x]!=x)return p[x]=find(p[x]);
    return p[x];
}
int main()
{
    cin>>n>>m>>vol;
    
    for(int i=1;i<=n;i++)p[i]=i;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
    
    while(m--)
    {
        int a,b;
        cin>>a>>b;
        int pa=find(a),pb=find(b);
        if(pa!=pb)
        {
            v[pb]+=v[pa];
            w[pb]+=w[pa];
            p[pa]=p[pb];
        }
    }
    
    //01背包
    for(int i=1;i<=n;i++)
        if(p[i]==i)//只有是根节点
            for(int j=vol;j>=v[i];j--)
                f[j]=max(f[j],f[j-v[i]]+w[i]);
    cout<<f[vol];
    return 0;
}

程序自动分析

思路
数据范围太大：需要离散化处理

由于约数条件顺序无所谓，所以先处理所有相等条件，相等条件直接一定不会出现矛盾。不等条件，如果xi和xj在同一集合当作，则已经矛盾。

1离散化
2将所有相等条件合并（并查集合并）
3依次判断每个不等条件（并查集查询）

代码

#include
using namespace std;
const int N=2e6+10;

int n,m;
int p[N];
unordered_map<int,int>S;
struct Query
{
    int x,y,e;
}query[N];

int get(int x)//离散化
{
    if(S.count(x)==0)S[x]=++n;
    return S[x];
}
int find(int x)
{
    if(p[x]!=x)return p[x]=find(p[x]);
    return p[x];
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        n=0;
        S.clear();
        scanf("%d",&m);
        for(int i=0;i<m;i++)
        {
            int x,y,e;
            scanf("%d%d%d",&x,&y,&e);
            query[i]={get(x),get(y),e};//离散化
        }
        
        for(int i=1;i<=n;i++)p[i]=i;
        
        for(int i=0;i<m;i++)
            if(query[i].e==1)//合并相等条件
            {
                int pa=find(query[i].x),pb=find(query[i].y);
                p[pa]=pb;
            }
        bool has_conflict=0;
        for(int i=0;i<m;i++)//判不等条件
            if(query[i].e==0)
            {
                int pa=find(query[i].x),pb=find(query[i].y);
                if(pa==pb)
                {
                    has_conflict=1;
                    break;
                }
            }
        if(has_conflict)puts("NO");
        else puts("YES");
    }    
    return 0;
}

银河英雄传说

思路
并查集维护距离
并查集的思想是以祖宗节点为代表，那么间隔舰数位
$max(0,abs(d[x]-d[y])-1)$
$d[x]$为x到祖宗节点距离，初值为0。那么我们如何维护它呢？

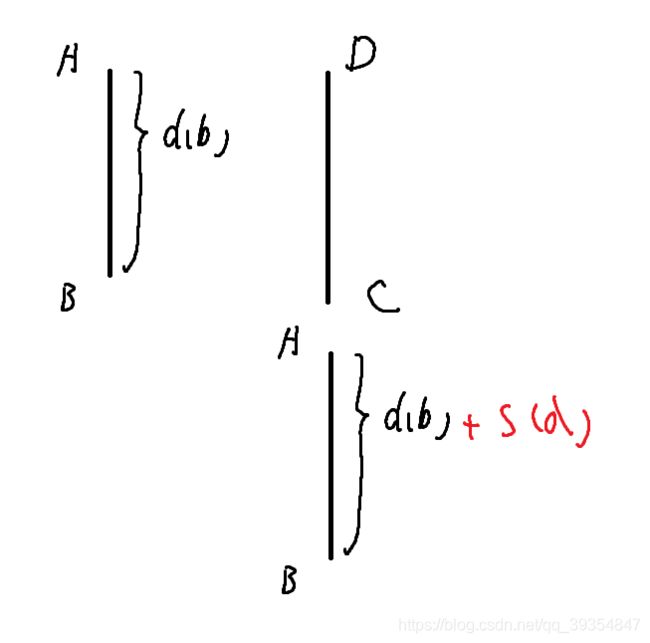
队列P:B到队头A的距离为d[B]
队列Q:C到队头D的共有s[D]个元素
将P接到Q下面，要维护更新P中各节点到新祖宗节点的距离，则每个节点加上s[D]，实际上要实现这一操作只需令P原来的祖宗节点距离更新为s[D],这样在find查询的时候就会更新，其他节点到新祖宗节点的距离，需要注意的是，我们还需要在更新距离后维护合并集合的size

只是合并，还没有查询的状态

代码

#include
using namespace std;

const int N=3e5+10;
int m;
int p[N],s[N],d[N];
int find(int x)
{
    if(p[x]!=x)
    {//回溯更新
        int root=find(p[x]);
        d[x]+=d[p[x]];//节点到祖宗节点距离=节点到父节点距离+父节点到祖宗节点距离
        p[x]=root;
    }
    return p[x];
}
int main()
{
    scanf("%d",&m);
    for(int i=1;i<N;i++)
    {
        p[i]=i;
        s[i]=1;
    }
    while(m--)
    {
        char op[2];
        int a,b;
        scanf("%s%d%d",op,&a,&b);
        if(op[0]=='M')
        {
            int pa=find(a),pb=find(b);
            d[pa]=s[pb];//其实相当于懒惰标记，后面更新有点像差分前缀和
            s[pb]+=s[pa];
            p[pa]=pb;
        }
        else
        {
            int pa=find(a),pb=find(b);
            if(pa!=pb)puts("-1");
            else printf("%d\n",max(0,abs(d[a]-d[b])-1));
        }
    }
    return 0;
}

奇偶游戏

思路
s[l~r]有奇数个1=s[r]-s[l-1]有奇数个1=s[r]和s[l-1]奇偶相同，反之不同
有没有撒谎就看有没有产生矛盾

带边权做法：

代码

#include
using namespace std;
const int N=2e5+10;//1e5个点可能由2e5个关系
int n,m;
int p[N],d[N];
unordered_map<int,int>S;

int get(int x)
{
    if(!S.count(x))S[x]=++n;
    return S[x];
}
int find(int x)
{
    if(p[x]!=x)
    {
        int root=find(p[x]);
        d[x]+=d[p[x]];
        d[x]%=2;//mod2意义下距离，如果不是mod2下面主函数维护距离也要这样
        p[x]=root;
    }
    return p[x];
}
struct Input
{
    int x,y,dis;
}In[N];
int main()
{
    cin>>n>>m;
    n=0;
    int res=m;
    for(int i=1;i<=m;i++)
    {
        int a,b,dis;
        string op;
        cin>>a>>b>>op;
        a--;
        if(op=="even")dis=0;
        else dis=1;
        In[i]={get(a),get(b),dis};
    }
    
    for(int i=1;i<=n;i++)p[i]=i;
    
    for(int i=1;i<=m;i++)
    {
        int x=In[i].x,y=In[i].y;
        if(In[i].dis)//异类
        {
            int px=find(x),py=find(y);
            if(px==py)
            {
                if((d[x]^d[y])==0)//别写成d[px]^d[py]
                {
                    res=i-1;
                    break;
                }
            }
            else
            {
                d[px]=d[x]^d[y]^1;//维护更新距离但和siz无光的例子
                p[px]=py;
            }
        }
        else//同类
        {
            int px=find(x),py=find(y);
            if(px==py)
            {
                if(d[x]^d[y])
                {
                    res=i-1;
                    break;
                }
            }
            else
            {
                d[px]=d[x]^d[y]^0;
                p[px]=py;
            }
        }
    }
    cout<<res;
    
    return 0;
}

扩展域解法

扩展域的元素是某一条件，当这些元素处于同一集合的时候，说明这些条件是可以互相推导出来的
代码

#include
using namespace std;
const int N=4e5+10;
int n,m;
int p[N];//2个扩展域开两倍
unordered_map<int,int>S;

int get(int x)
{
    if(!S.count(x))S[x]=++n;
    return S[x];
}
int find(int x)
{
    if(p[x]!=x)return p[x]=find(p[x]);
    return p[x];
}
struct Input
{
    int x,y,dis;
}In[N];
int main()
{
    cin>>n>>m;
    n=0;
    int res=m;
    for(int i=1;i<=m;i++)
    {
        int a,b,dis;
        string op;
        cin>>a>>b>>op;
        a--;
        if(op=="even")dis=0;
        else dis=1;
        In[i]={get(a),get(b),dis};
    }
    
    for(int i=1;i<=2*n;i++)p[i]=i;//开两倍初始化
    
    for(int i=1;i<=m;i++)
    {
        int x=In[i].x,y=In[i].y;
        int px=find(x),py=find(y),pxn=find(x+n),pyn=find(y+n);
        if(In[i].dis)
        {
            if(px==py||pxn==pyn)//先判矛盾
            {
                res=i-1;
                break;
            }
            else 
            {
                if(px!=pyn)p[px]=pyn;
                if(py!=pxn)p[py]=pxn;
            }
        }
        else
        {
            if(px==pyn||py==pxn)
            {
                res=i-1;
                break;
            }
            else
            {
                if(px!=py)p[px]=py;
                if(pxn!=pyn)p[pxn]=pyn;
            }
        }
    }
    cout<<res;
    
    return 0;
}

总结

并查集主要用于解决无向图，题目常常给出具有双向传递性的关系，并且这些关系可以相互推导。我们首先要挖掘关系之间是如何传递的，再利用并查集解决问题。

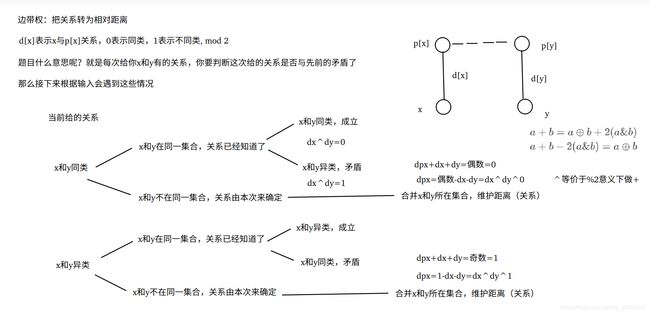
边带权：把信息蕴含到边权之中，处于同一集合的元素表明具有关系
扩展域：把条件本身作为元素，处于同一集合的元素表明对应的条件可以相互推导

数据处理：离散化，N个点要开2×N p[x]数组，扩展域在2XN基础上再×扩展域数量（初始化的时候也别忘记）

信息维护
维护集合大小，当单个体积为1时，体积=个数
维护距离（边权），通常更新距离更新在每个集合祖宗节点（相当于lazy标记，或者差分），在find的时候子节点会随之更新。需要注意的是距离的维护未必和体积相关，需要对应题目来变化

细节：如果做边带权去做取模运算，需要注意main函数和find函数边权更新的时候都要取模，如果涉及减法运算需要加上模数防止出现负数