期望最大化注意力网络用于语义分割——Expectation-Maximization Attention Networks for Semantic Segmentation
0.摘要
自注意机制已广泛应用于各种任务。它的设计是通过所有位置的特征的加权和来计算每个位置的表示。因此,它可以捕捉计算机视觉任务的长程关系。然而,这种方法在计算上是耗费资源的,因为注意力图是相对于所有其他位置计算的。在本文中,我们将注意机制形式化为期望最大化的方式,并迭代地估计一组更紧凑的基础,基于这些基础计算注意力图。通过对这些基础的加权求和,得到的表示是低秩的,并且将输入中的噪声信息降低。所提出的期望最大化注意力(EMA)模块对输入的方差具有鲁棒性,并且在内存和计算方面也很友好。此外,我们建立了基础维护和规范化方法来稳定其训练过程。我们在流行的语义分割基准数据集,包括PASCAL VOC、PASCAL Context和COCO Stuff上进行了广泛的实验,在这些数据集上创造了新的记录。
1.引言
语义分割是计算机视觉中的一个基本且具有挑战性的问题,其目标是为图像的每个像素分配一个语义类别。它对于各种任务非常重要,例如自动驾驶、图像编辑和机器人感知。为了有效地完成语义分割任务,我们需要区分一些混淆的类别并考虑不同对象的外观。例如,“草”和“地面”在某些情况下颜色相似,“人”可能在图像的不同位置具有不同的比例、形状和服装。同时,输出的标签空间非常紧凑,特定数据集的类别数量有限。因此,这个任务可以被视为将高维噪声空间中的数据点投影到一个紧凑的子空间中。其实质在于去除这些变化中的噪声并捕捉最重要的语义概念。
最近,许多基于全卷积网络(FCNs)[22]的最先进方法已被提出来解决上述问题。由于固定的几何结构,它们本质上受到局部感受野和短程上下文信息的限制。为了捕捉长程依赖关系,一些作品采用了多尺度上下文融合[17],例如astrous卷积[4]、空间金字塔[37]、大卷积核卷积[25]等等。此外,为了保留更详细的信息,提出了编码器解码器结构[34,5]以融合中等级和高级语义特征。为了聚合所有空间位置的信息,使用了注意机制[29,38,31],这使得单个像素的特征可以融合来自所有其他位置的信息。然而,原始的基于注意力的方法需要生成一个大的注意力图,这具有高计算复杂度并占用大量GPU内存。瓶颈在于注意力图的生成和使用都是相对于所有位置计算的。
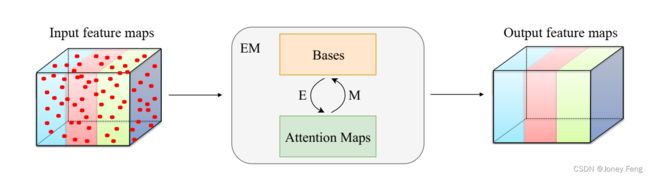
针对上述问题,本文从期望最大化(EM)算法[7]的角度重新思考注意力机制,并提出了一种新的基于注意力的方法,即期望最大化注意力(EMA)。我们不像之前的方法[38,31]将所有像素本身视为重构基础,而是使用EM算法找到一个更紧凑的基础集,可以大大减少计算复杂度。具体而言,我们将构建基础视为在EM算法中要学习的参数,并将注意力图视为潜在变量。在这种设置下,EM算法旨在找到参数(基础)的最大似然估计。给定当前参数,Expectation(E)步骤用于估计注意力图的期望,而Maximization(M)步骤用于通过最大化完整数据似然函数来更新参数(基础)。E步骤和M步骤交替执行,直到收敛。在收敛后,输出可以计算为基础的加权和,其中权重为规范化后的最终注意力图。EMA的流程如图1所示。我们进一步将提出的EMA方法嵌入到神经网络模块中,命名为EMA单元。EMA单元可以简单地通过常用操作实现。它还非常轻量级,可以轻松嵌入到现有的神经网络中。此外,为了充分利用其容量,我们还提出了两种方法来稳定EMA单元的训练过程。我们还在三个具有挑战性的数据集上评估了其性能。
本文的主要贡献如下: •我们将自注意力机制重新定义为期望最大化迭代方式,可以学习一个更紧凑的基础集,并大大减少计算复杂度。据我们所知,这是第一次将EM迭代引入到注意力机制中。 •我们将所提出的期望最大化注意力构建为神经网络的轻量级模块,并建立了特定的基础维护和规范化方式。 •在三个具有挑战性的语义分割数据集(包括PASCAL VOC、PASCAL Context和COCO Stuff)上进行了广泛的实验,证明了我们的方法优于其他最先进的方法。
图1:所提出的期望最大化注意力方法的流程。
2.相关工作
语义分割。基于全卷积网络(FCN)[22]的方法通过利用预先在大规模数据上进行预训练的分类网络[14,15,33]强大的卷积特征,在图像语义分割方面取得了巨大的进展。为了增强多尺度上下文聚合,提出了几种模型变种。例如,DeeplabV2 [4]利用星型空间金字塔池化(ASPP)嵌入上下文信息,其中包括具有不同扩张率的并行扩张卷积。DeeplabV3 [4]通过图像级特征扩展ASPP以进一步捕捉全局上下文。同时,PSPNet [37]提出了金字塔池化模块来收集不同尺度的上下文信息。GCN [25]采用大卷积核卷积的解耦来获得特征图的大接受野,并捕获长距离信息。对于另一类变种,它们主要关注于预测更详细的输出。这些方法基于U-Net [27],结合高级特征和中级特征的优点。RefineNet [21]利用拉普拉斯图像金字塔明确地捕获下采样过程中可用信息,并从粗到细输出预测。DeeplabV3+ [5]在DeeplabV3上添加了一个解码器,以特别改善沿着物体边界的分割结果。Exfuse [36]提出了一个新的框架,以弥合低级特征和高级特征之间的差距,从而提高了分割质量。
注意力模型。注意力在各种任务中得到了广泛应用,如机器翻译、视觉问答和视频分类。自注意力方法[2,29]通过对句子中所有位置的嵌入进行加权求和,计算出一个位置的上下文编码。Non-local[31]首次将自注意力机制作为计算机视觉任务的模块,如视频分类、物体检测和实例分割。PSANet [38]通过预测的注意力图来学习聚合每个位置的上下文信息。A2Net [6]提出了双重注意块,从整个时空图像空间中分发和收集信息丰富的全局特征。DANet [11]应用空间和通道注意力来聚集特征图周围的信息,其计算和存储代价甚至比Non-local方法还要高。我们的方法受到以上工作中注意力机制的成功启发。我们从EM算法的视角重新思考注意力机制,并以EM算法的迭代方式计算注意力图。
3.预备知识
在介绍我们提出的方法之前,我们首先回顾三种高度相关的方法,即EM算法、高斯混合模型和非局部模块。
3.1.期望最大化算法
期望最大化(EM)[7]算法旨在为潜变量模型寻找最大似然解。将X = {x1,x2,...,xN}表示为数据集,其中包含N个观测样本,每个数据点xi都有其相应的潜在变量zi。我们称{X,Z}为完整数据,其似然函数的形式为ln p(X,Z | θ),其中θ是模型的所有参数集。在实践中,我们只能通过后验分布p(Z | X,θ)来了解Z中的潜在变量知识。EM算法旨在通过两个步骤,即E步和M步,最大化似然ln p(X,Z | θ)。在E步中,我们使用当前参数θold来找到由p(X,Z | θ)给出的Z的后验分布。然后,我们使用后验分布来计算完整数据似然的期望Qθ,θold,它由以下式子给出:Qθ,θold=X z p Z|X,θoldln p(X,Z | θ)。 (1)然后,在M步中,通过最大化函数来确定修订后的参数θnew:θnew = arg max θQθ,θold。 (2)EM算法交替执行E步和M步直到满足收敛条件。
3.2.高斯混合模型
在实际应用中,我们可以简单地将Σk替换为单位矩阵I,并将上述方程中的Σk省略。
3.3.非局部
非局部模块[31]的功能与自注意力机制相同。它可以表示为: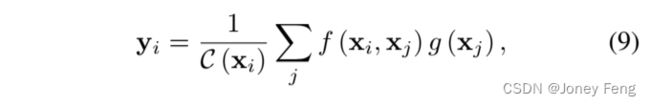 ,其中f(·,·)表示一般的核函数,C(x)是一个归一化因子,xi表示位置i的特征向量。由于这个模块应用于卷积神经网络(CNN)的特征图上,考虑到式(5)中的N(xn|µk,Σk)是xn和µk之间的特定核函数,式(8)只是式(9)的一个特定设计。因此,从GMM的视角来看,非局部模块只是对X进行重新估计,没有E步和M步。具体来说,µ只是在非局部模块中选择的X。在GMM中,高斯基数是手动选择的,通常满足K ≪ N。但在非局部模块中,基数是选择为数据本身,因此K = N。非局部模块有两个明显的缺点。首先,数据位于低维流形中,因此基数过多。其次,计算开销大,内存成本也很大。
,其中f(·,·)表示一般的核函数,C(x)是一个归一化因子,xi表示位置i的特征向量。由于这个模块应用于卷积神经网络(CNN)的特征图上,考虑到式(5)中的N(xn|µk,Σk)是xn和µk之间的特定核函数,式(8)只是式(9)的一个特定设计。因此,从GMM的视角来看,非局部模块只是对X进行重新估计,没有E步和M步。具体来说,µ只是在非局部模块中选择的X。在GMM中,高斯基数是手动选择的,通常满足K ≪ N。但在非局部模块中,基数是选择为数据本身,因此K = N。非局部模块有两个明显的缺点。首先,数据位于低维流形中,因此基数过多。其次,计算开销大,内存成本也很大。
4.期望最大注意力
考虑到注意力机制的高计算复杂度和非局部模块的限制,我们首先提出了期望最大化注意力(EMA)方法,它是自我关注的增强版本。与选择所有数据点作为基数的非局部模块不同,我们使用EM迭代来找到一个紧凑的基数集。为简化符号,我们将大小为C×H×W的输入特征图X从单个样本中重新塑造为N×C,其中N=H×W,xi∈RC索引像素i处的C维特征向量。我们提出的EMA包括三个操作,包括责任估计(AE),似然最大化(AM)和数据重新估计(AR)。简单地说,给定输入X∈RN×C和初始基数µ∈RK×C,AE估计潜在变量(或“责任”)Z∈RN×K,因此它作为EM算法中的E步骤。AM使用该估计来更新基数µ,它作为M步骤。AE和AM步骤交替执行预先指定的迭代次数。然后,使用收敛的µ和Z,AR将原始X重构为Y并输出它。
已经证明,随着EM步骤的迭代,完整数据似然ln p(X,Z)会单调增加。由于可以通过对Z进行边缘化的方式来估计ln p(X),因此最大化ln p(X,Z)是最大化ln p(X)的代理。因此,随着AE和AM的迭代,更新的Z和µ能够更好地重构原始数据X。重构的X˜可以尽可能多地捕捉X中的重要语义。此外,与非局部模块相比,EMA为输入图像的像素找到了一个紧凑的基数集。紧凑性是非平凡的。由于K ≪ N,X˜位于X的子空间中。这种机制消除了许多不必要的噪声,并使每个像素的最终分类更易处理。此外,此操作将复杂度(空间和时间)从O(N^2)降低到O(NKT),其中T是AE和AM的迭代次数。EM算法的收敛也是有保证的。值得注意的是,在我们的实验中,EMA仅需要三次迭代即可获得良好的结果。因此,T可以被视为一个小常数,这意味着复杂度只有O(NK)。
 图2:提出的EMAU的总体结构。关键组件是EMA操作符,在其中AE和AM交替执行。除了EMA操作符之外,我们在EMA的开头和结尾添加了两个1×1卷积,并将输出与原始输入相加,形成类似残差的块。最好在屏幕上查看。
图2:提出的EMAU的总体结构。关键组件是EMA操作符,在其中AE和AM交替执行。除了EMA操作符之外,我们在EMA的开头和结尾添加了两个1×1卷积,并将输出与原始输入相加,形成类似残差的块。最好在屏幕上查看。
4.1.责任评估
责任估计(AE)作为EM算法中的E步骤。这一步计算znk的期望值,它对应于第k个基数µ对xn的责任,其中1≤k≤K,1≤n≤N。我们将给定µk的xn的后验概率表示为:p(xn|µk)=K(xn,µk),其中K表示一般的核函数。现在,式(5)可以被重新表述为更一般的形式: K(a,b)有几种选择,例如内积a⊤b,指数内积exp(a⊤b),欧氏距离ka−bk2/2,RBF核exp[−ka−bk2/σ2]等等。与非局部模块进行比较,这些函数的选择对最终结果的影响微不足道。因此,在我们的论文中,我们简单地采用了指数内积exp(a⊤b)。在实验中,式(11)可以实现为一个矩阵乘法加上一个softmax层。总之,在第t次迭代中,AE的操作可以表示为:
K(a,b)有几种选择,例如内积a⊤b,指数内积exp(a⊤b),欧氏距离ka−bk2/2,RBF核exp[−ka−bk2/σ2]等等。与非局部模块进行比较,这些函数的选择对最终结果的影响微不足道。因此,在我们的论文中,我们简单地采用了指数内积exp(a⊤b)。在实验中,式(11)可以实现为一个矩阵乘法加上一个softmax层。总之,在第t次迭代中,AE的操作可以表示为:
4.2.似然函数最大化
似然最大化(AM)作为EM算法的M步骤。使用估计的Z,AM通过最大化完整数据似然更新µ。为了使基数保持在与X相同的嵌入空间中,我们使用X的加权求和来更新基数µ。因此,µk的更新为: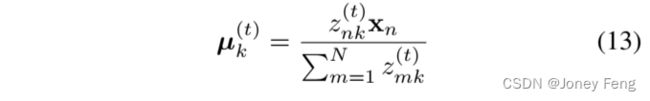
在AM的第t次迭代中。值得注意的是,如果我们在式(12)中将λ→∞,那么{zn1,zn2,···,znK}将成为一个one-hot嵌入。在这种情况下,每个像素仅分配给一个基数。并且基数由分配给它的那些像素的平均值进行更新。这就是K均值聚类算法[10]的做法。因此,AE和AM的迭代也可以视为K均值聚类的软版本。
4.3.数据重评估
EMA交替运行AE和AM共T次。在此之后,最终的µ(T)和Z(T)被用来重新估计X。我们采用式(8)构建新的X,即X˜,其表示为:X˜=Z(T)µ(T)。(14)由于X˜是由一个紧凑的基数集构建的,与输入X相比,它具有低秩特性。我们在图2中展示了X˜的一个例子。显然,从AR输出的X˜在特征空间中非常紧凑,并且物体内部的特征方差小于输入的特征方差。
5.EMA单元
为了更好地将提出的EMA与深度神经网络相结合,我们进一步提出了期望最大化注意力单元(EMAU)并将其应用于语义分割任务。在本节中,我们将详细描述EMAU。我们首先介绍EMAU的总体结构,然后讨论基数维护和归一化机制。
5.1.EMA单元的结构
EMAU的总体结构如图2所示。EMAU乍一看类似于ResNet的瓶颈结构,但它用EMA操作替换了繁重的3×3卷积。首先,没有ReLU激活的第一个卷积被添加,以将输入的值范围从(0,+∞)转换为(−∞,+∞)。这种转换非常重要,否则估计的µ(T)也将在[0,+∞)范围内,与一般卷积参数相比,其容量减半。最后,插入一个1×1卷积将重新估计的X˜转换为X的残差空间。对于AE、AM和AR步骤中的每一个,计算复杂度为O(NKC)。由于我们设置K ≪ C,因此几次AE和AM的迭代加上一个AR只是与输入和输出通道数均为C的1×1卷积相同数量级。加上两个1×1卷积的额外计算,EMAU的整个FLOPs大约是运行具有相同输入和输出通道数的3×3卷积的模块的1/3。此外,EMA维护的参数仅计数为KC。
5.2.基础维护
EM算法的另一个问题是基数的初始化。EM算法有保证收敛,因为完整数据的可能性是有限的,并且在每次迭代中,E和M步骤都会提高其当前的下限。然而,不能保证收敛到全局最大值。因此,在迭代之前基数的初始值非常重要。我们上面只描述了如何使用EMA处理一张图像。然而,对于计算机视觉任务,数据集中有成千上万的图像。由于每个图像X具有不同的像素特征分布,因此不适合使用在一个图像上计算出的µ来重建其他图像的特征图。因此,我们对每个图像运行EMA。
对于第一个小批量,我们使用Kaiming的初始化[13]初始化µ(0),其中我们将矩阵乘法视为1×1卷积。对于接下来的小批量,一种简单的选择是使用标准反向传播更新µ(0)。然而,由于AE和AM的迭代可以展开成一个递归神经网络(RNN),通过它们传播的梯度将遇到消失或爆炸问题。因此,µ(0)的更新是不稳定的,EMA单元的训练过程可能会崩溃。在本文中,我们在训练过程中使用移动平均更新µ(0)。在迭代图像之后,生成的µ(T)可以被视为µ(0)的有偏更新,其中偏差来自于图像采样过程。为了使其偏差较小,我们首先在小批量上对µ(T)进行平均,得到µ¯(T)。然后我们将µ(0)更新为:µ(0)←αµ(0)+(1−α)µ¯(T)(15),其中α∈[0,1]是动量。对于推理,µ(0)保持不变。这种移动平均机制也适用于批归一化(BN)[16]。
5.3.基础规范化
在上面的子段中,我们完成了每个小批量µ(0)的维护。然而,由于RNN的缺陷,AE和AM迭代中µ(t)的稳定更新仍然无法保证。上述移动平均机制要求µ¯(T)与µ(0)没有显着差异,否则它也会像反向传播一样崩溃。这个要求还限制了µ(t)的值范围,1≤t≤T。为此,我们需要对µ(t)应用归一化。乍一看,批归一化(BN)或层归一化(LN)[1]似乎是不错的选择。然而,这些归一化方法会改变每个基础µ(kt)的方向,从而改变它们的属性和语义含义。为保持每个基向量的方向不变,我们选择欧几里得归一化(L2Norm),它通过其长度将每个µ(kt)除以其长度。通过应用它,µ(t)位于K维联合超球体上,nµ(0)k,µ(1)k,···,µ(kT)o的序列在其上形成轨迹。
5.4.与双重注意力进行比较
A2Net [6] 提出了双重注意力块(A2 block),其中输出Y计算如下:Y = hφ(X,Wφ)sfm(θ(X,Wθ))⊤isfm(ρ(X,Wρ)),(16)其中sfm表示softmax函数。φ,θ和ρ分别表示具有卷积核Wφ,Wθ和Wρ的三个1×1卷积。如果我们在θ和ρ之间共享参数,则可以将Wθ和Wρ都标记为µ。可以看出,sfm(θ(X,Wθ))仅计算与公式(5)相同的Z,并且那些位于[·]内的变量更新µ。整个A2块的过程等同于只有一个迭代的EMA。A2块中的Wθ通过反向传播进行更新,而我们的EMAU通过移动平均进行更新。总之,双重注意力块可以被视为EMAU的一种特殊形式。
图3:EMAU基向量维护策略(左)和归一化(右)的消融研究。实验在PASCAL VOC数据集上使用ResNet-50,批量大小为12,训练输出步幅为16进行。训练的迭代次数T设置为3。最佳查看屏幕。
6.实验
为了评估所提出的EMAU,我们在PASCAL VOC数据集[9]、PASCAL Context数据集[24]和COCO Stuff数据集[3]上进行了广泛的实验。在本节中,我们首先介绍实现细节。然后我们进行消融研究,以验证所提出方法在PASCAL VOC数据集上的优越性。最后,我们报告了在PASCAL Context数据集和COCO Stuff数据集上的结果。
6.1.实现细节
我们使用在ImageNet [28]上预训练的ResNet [14]作为我们的骨干网络。遵循先前的工作[37,4,5],我们采用多项式学习率策略,其中初始学习率在每个迭代后乘以(1-iter/total iter)0.9。所有数据集的初始学习率均设置为0.009。动量和权重衰减系数分别设置为0.9和0.0001。对于数据增强,我们应用常见的缩放(0.5到2.0)、裁剪和图像翻转来增强训练数据。所有数据集的输入大小均设置为513×513。在所有实验中,采用了同步批归一化和多网格[4]。对于评估,我们采用常用的平均交并比指标。在PASCAL VOC和PASCAL Context上训练时,骨干网络的输出步幅设置为16,在COCO Stuff上训练并在所有数据集上评估时,输出步幅设置为8。为了加快训练过程,我们在ResNet-50 [14]上进行所有消融研究,批量大小为12。对于与最先进技术进行比较的所有模型,我们在ResNet-101上进行训练,批量大小为16。我们在PASCAL VOC和COCO Stuff上训练30K次迭代,在PASCAL Context上训练15K次迭代。我们使用3×3卷积将通道数从2,048降至512,然后在其上堆叠EMAU。我们将整个网络称为EMANet。我们将基数目K设置为64,λ设置为1,迭代次数T设置为3作为默认值进行训练。
图4:迭代次数T的消融研究。实验在PASCAL VOC数据集上使用ResNet-50,训练输出步幅为16,批量大小为12进行。
6.2.在PASCAL VOC 数据集上的结果
6.2.1.基础维护和规范化
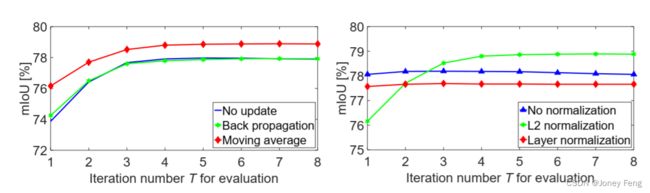
在这部分中,我们首先比较了不同维护µ(0)策略的表现。我们在训练中设置T=3,在评估中设置1≤T≤8。如图3左侧所示,所有策略的性能随着AE和AM的迭代次数增加而提高。当T≥4时,从更多迭代中获得的收益变得微不足道。移动平均是它们中表现最好的。它在所有迭代中均获得最高的性能,并且在mIoU上至少超过其他方法0.9。令人惊讶的是,与不更新相比,反向传播更新并没有表现出优势,甚至在T≥3时表现更差。然后,我们将性能与无归一化、LN和L2Norm进行比较,如上所述。从图3右侧可以清楚地看到,LN甚至比无归一化还要差。由于它可以部分缓解类似RNN结构的梯度问题。LN和无归一化的性能与迭代次数T几乎没有关联。相比之下,L2Norm的性能随着迭代次数变大而增加,当T≥3时,它的性能超过LN和无归一化。
6.2.2.迭代次数的消融研究
从图3可以看出,在评估过程中,EMAU的性能随着更多迭代次数的增加而提高,当T>4时,增益变得微不足道。在本小节中,我们还研究了训练中T的影响。我们将Ttrain和T eval的性能矩阵绘制成图4。从图4可以清楚地看出,无论Ttrain是什么,mIoU随着更多迭代次数的增加而单调增加。它们最终会收敛到一个固定的值。然而,这个规律在训练中并不适用。mIoU在Ttrain=3时达到峰值,并随着更多迭代次数的减少而下降。这种现象可能是由EMAU的类似RNN行为造成的。尽管移动平均和L2Norm可以在一定程度上缓解这个问题,但问题仍然存在。我们还在A2块[6]上进行了实验,它可以被视为EMAU在第5.4节中提到的一种特殊形式。同样,非局部模块也可以被视为没有AM步骤的EMAU的一种特殊形式,其中包括更多的基数和Ttrain=1。在相同的骨干网络和训练调度程序下,A2块在mIoU上达到77.41%,非局部模块在mIoU上达到77.78%,而EMANet在Ttrain = 1和T eval = 1时达到77.34%。这三个结果具有很小的差异,与我们的分析相符。
表1:在PASCAL VOC上使用ResNet-101和输出步幅8进行DeeplabV3 / V3 +和PSANet的mIoU(%)详细比较。FLOPs和内存是使用输入尺寸513×513计算的。SS:测试期间的单尺度输入。MS:多尺度输入。Flip:添加左右翻转的输入。EMANet(256)和EMANet(512)分别表示输入通道数为256和512的EMANet。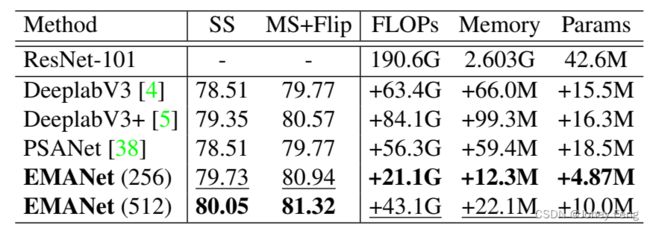
表3:在PASCAL Context测试集上与现有技术的比较。“+”表示在COCO Stuff上进行了预训练。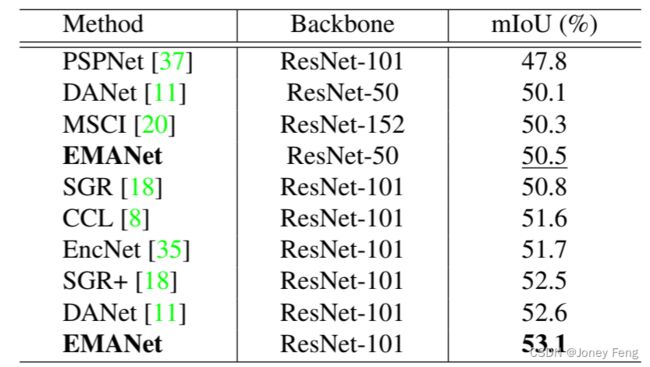 表4:在COCO Stuff测试集上的比较。
表4:在COCO Stuff测试集上的比较。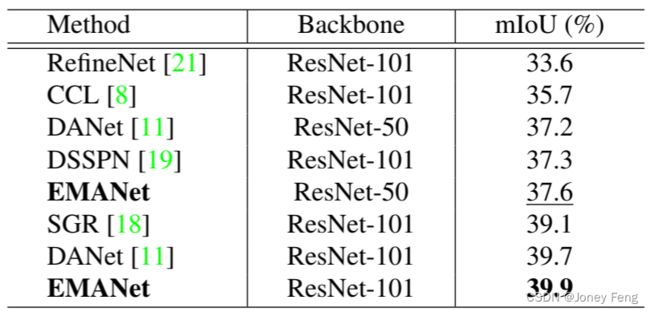
6.2.3.与最先进方法的比较
我们首先在验证集上彻底比较了EMANet与三个基线模型,即DeeplabV3,DeeplabV3 +和PSANet。我们在表1中报告了mIoU,FLOPs,内存成本和参数数量。我们可以看到,EMANet在性能上大大优于这三个基线模型。此外,EMANet的计算和内存负担要轻得多。我们进一步在PASCAL VOC测试集上将我们的方法与现有方法进行比较。按照先前的方法[4,5],我们依次在COCO,VOC trainaug和VOC trainval集上训练EMANet。我们分别将基本学习速率设置为0.009,0.001和0.0001。我们在COCO上进行了150K次迭代,在最后两轮中进行了30K次迭代。在对测试集进行推断时,我们利用了多尺度测试和左右翻转。如表2所示,我们的EMANet在PASCAL VOC上创下了新纪录,并在mIoU上提高了DeeplabV3 [4]相同骨干的2.0%。我们的EMANet在使用ResNet-101骨干网络的网络中表现最佳,并比以前最佳的结果提高了0.9%,这是非常显著的,因为这个基准非常具有竞争力。此外,它实现了与基于一些更大的骨干网络的方法相当的性能。 图5:最后一次迭代时责任Z的可视化。前两行说明了来自PASCAL VOC验证集的两个示例。最后两行说明了来自PASCAL Context验证集的两个示例。z·i表示第i个基的责任,在最后一次迭代中分配给所有像素。i,j,k和l是四个随机选择的索引,其中1≤i,j,k,l≤K。最好在屏幕上查看。
图5:最后一次迭代时责任Z的可视化。前两行说明了来自PASCAL VOC验证集的两个示例。最后两行说明了来自PASCAL Context验证集的两个示例。z·i表示第i个基的责任,在最后一次迭代中分配给所有像素。i,j,k和l是四个随机选择的索引,其中1≤i,j,k,l≤K。最好在屏幕上查看。
6.3.在PASCAL Context数据集上的结果
为验证我们提出的EMANet的泛化能力,我们在PASCAL Context数据集上进行了实验。PASCAL Context的定量结果显示在表3中。据我们所知,基于ResNet-101的EMANet在PASCAL Context数据集上取得了最高的性能。即使在额外数据(COCO Stuff)上进行了预训练,SGR +仍然不及EMANet。
6.4.在COCO stuff 数据集上的实验结果
为进一步评估我们方法的有效性,我们还在COCO Stuff数据集上进行了实验。与先前最先进方法的比较结果显示在表4中。值得注意的是,EMANet在mIoU达到了39.9%,并大幅胜过以前的方法。
6.5.基础责任的可视化
为了更深入地理解我们提出的EMAU,我们在图5中可视化了迭代的责任映射Z。对于每个图像,我们随机选择了四个基础(i,j,k和l),并显示它们在最后一次迭代中所有像素的相应责任。显然,每个基础对应于图像的一个抽象概念。随着迭代AE和AM的进展,抽象概念变得更加紧凑和清晰。正如我们所看到的,这些基础会收敛到一些特定的语义,而不仅仅关注前景和背景。具体而言,前两行的基础专注于特定的语义,例如人类、酒杯、餐具和剖面。最后两行的基础专注于帆船、山脉、飞机和车道。
7.总结
在本文中,我们提出了一种新型的注意力机制,即期望最大化注意力(EMA),它通过迭代执行EM算法计算出更紧凑的基础集。EMA的重建输出是低秩的,并且对输入的变化具有鲁棒性。我们将所提出的方法形式化为轻量级模块,可以轻松插入到现有的CNN中,代价很小。在许多基准数据集上的广泛实验表明了所提出的EMAU的有效性和效率。